Системы линейных уравнений с постоянными коэффициентами, методы их решения.

Лекция 23.

Определение 23.1. Система дифференциальных уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных.

В частности, система линейных уравнений первого порядка с постоянными коэффициентами имеет вид:

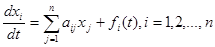. (23.1)

Можно использовать матричную запись такой системы, если ввести матрицы

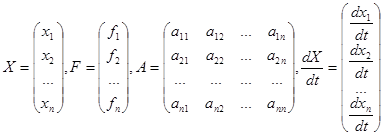. Тогда системе (23.1) эквивалентно матричное уравнение 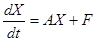. (23.2)

Если же рассмотреть линейный оператор 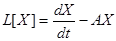, уравнение (23.2) примет вид:

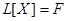. (23.3)

Так как оператор L обладает свойствами линейности:

1) L[cX] = cL[X];

2) L[X₁ + X₂] = L[X₁] + L[X₂],

то для решений линейной однородной системы (23.3) (при F = 0) справедливы те же свойства: если Х₁ и Х₂ – решения однородного уравнения (23.3) , то и их линейная комбинация будет решением того же уравнения.

Можно ввести понятие линейной зависимости решений Х₁, Х₂,…, Х_п:

Определение 23.2. Векторы (столбцы) Х₁, Х₂,…, Х_п , где

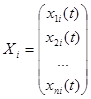, называются линейно зависимымипри 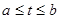, если существуют числа α₁,α₂,…, α_п, не все равные нулю, что

α₁Х₁ + α₂Х₂ +…+ α_пХ_п ≡ 0 (23.4)

при 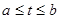. Если же тождество (23.4) справедливо только при всех α_i = 0, векторы называются линейно независимыми.

Замечание. Назовем определителем Вронского для уравнения (23.4) определитель вида

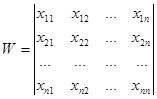, (23.5)

являющийся определителем системы уравнений, получаемых при координатной записи равенства (23.4). Можно показать, что так же, как и в случае решения линейного однородного уравнения, при W = 0 решения Х₁, Х₂,…, Х_п линейно зависимы на [a,b]. Тогда справедлива следующая теорема:

Теорема 23.1. Линейная комбинация 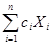п линейно независимых решений линейной однородной системы является общим решением этой системы.

Будем искать фундаментальную систему решений линейной однородной системы с постоянными коэффициентами

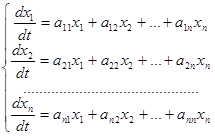(23.6)

в виде: 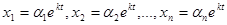, (23.7)

где α_i – постоянные. Подставив (23.7) в (23.6) и сократив на e^kt, получим:

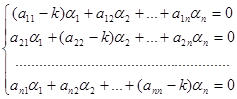. (23.8)

Для того, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы ее главный определитель был равен нулю:

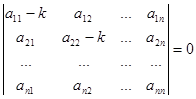, (23.9)

что представляет собой уравнение п – й степени относительно k, называемое характеристическим.

Если все корни характеристического уравнения различны, то, подставляя их последовательно в систему (23.8), можно найти соответствующие им значения 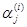и тем самым п различных решений системы (23.6). Эти решения линейно независимы. Действительно, если бы существовали числа β₁, β₂,…, β_п такие, что

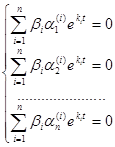, то в силу линейной независимости функций 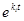отсюда следовало бы, что 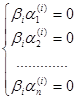для каждого i. Но поскольку хотя бы одно из 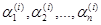не равно нулю, получаем, что все 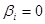. Следовательно, найденные решения (23.7) линейно независимы, и общее решение системы имеет вид: 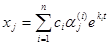, (23.10)

где c_i – произвольные постоянные.

Пример.

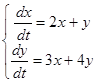. Составим характеристическое уравнение: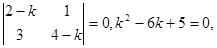

k₁ = 1, k₂ =5. Для k = 1 получаем систему для определения 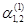: 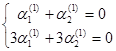, то есть

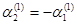. Примем 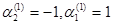, тогда 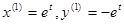. При k = 5 ,

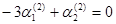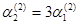. Тогда 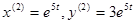. Следовательно, общее решение системы имеет вид: .

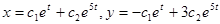В случае кратных корней характеристического уравнения решение системы (23.6) имеет вид

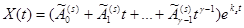, где γ – кратность корня k_s.

Пример.

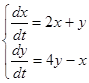. Характеристическое уравнение имеет вид: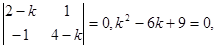

k₁ = k₂ = 3. Пусть x = (c₁ + c₂ t)e^3t, y = (c₃ + c₄ t)e^3t. Выразим постоянные с₃ и с₄ через с₁ и с₂. Для этого подставим найденные решения в одно из уравнений системы и приравняем коэффициенты при e^3t и te^3t: (3c₁ + c₂ + 3c₂t)e^3t = (2c₁ + c₃)e^3t + (2c₂ + c₄)te^3t, c₃ = c₁ + c₂,

c₄ = c₂. Итак, общее решение системы получено в форме: x = (c₁ + c₂ t)e^3t, y = (c₁+ с₂ + c₂t)e^3t.

Замечание. Для неоднородной системы (23.1) общим решением, так же как для неоднородного уравнения, будет сумма общего решения соответствующей однородной системы и частного решения неоднородной системы. При подборе частных решений справедлив принцип суперпозиции.

Пример.

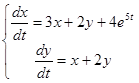. Найдем частное решение в виде: 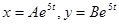. При подстановке получим: 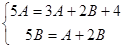, откуда А = 3, В = 1. Прибавив к полученному частному решению общее решение соответствующей однородной системы, запишем общее решение исходной системы: x = c₁e^t + 2c₂e^4t + 3e^5t, y = -c₁e^t + c₂e^4t + e^5t.

Лекция 24.

Устойчивость решений дифференциальных уравнений и их систем. Определение устойчивости по Ляпунову и асимптотической устойчивости. Автономные системы дифференциальных уравнений. Фазовое пространство (плоскость), фазовая траектория. Точки покоя. Классификация точек покоя системы двух однородных линейных дифференциальных уравнений с постоянными коэффициентами. Условия устойчивости точки покоя.

Поскольку при решении реальных задач с помощью дифференциальных уравнений начальные условия обычно являются результатами измерений и, следовательно, получены с некоторой погрешностью, очень важным является вопрос о том, как изменится решение уравнения при малом изменении начальных условий. В частности, если такие изменения существенно меняют решение, то подобное решение, очевидно, не имеет практической ценности.

Пусть некоторое явление описывается системой дифференциальных уравнений

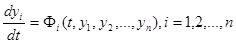(24.1)

с начальными условиями y_i(t₀) = y_i0 .

Определение 24.1. Решение φ_i (t) (ǐ = 1,2,…,n) называется устойчивым по Ляпунову, если

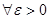
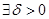такое, что для всякого решения y_i (t) той же системы, начальные условия которого удовлетворяют неравенствам 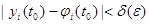, для всех 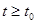справедливы неравенства 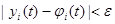(24.2)

(то есть близкие по значениям решения остаются близкими для всех ).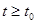

Если хотя бы для одного решения y_i (t) неравенства (24.2) не выполняются, решение φ_i (t) называется неустойчивым.

Если решение φ_i (t) не только устойчиво по Ляпунову, но и удовлетворяет условию

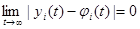(24.3)

при 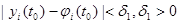, то это решение называется асимптотически устойчивым.

Замечание. Одно условие (24.3) не обеспечивает устойчивость решения.

Фазовая плоскость.

Дифференциальное уравнение второго порядка

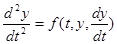(24.4)

равносильно системе уравнений первого порядка

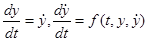. (24.5)

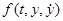Геометрически общее решение уравнения (24.4) или системы (24.5) можно представить семейством фазовых траекторий на фазовой плоскости .Особенно удобно такое представление в случае, когда функция не содержит явным образом независимого переменного t. Тогда система (24.5) имеет вид

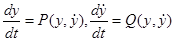(24.6)

и называется автономной системой. Фазовые траектории в этом случае удовлетворяют дифференциальному уравнению первого порядка

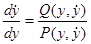, (24.7)

которое каждой точке ставит в соответствие наклон проходящей через нее интегральной кривой.

Точки покоя.

Определение 24.2. Точка 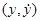фазовой плоскости системы (24.6) называется обыкновенной точкой, есл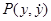и и 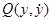дифференцируемы и не обращаются одновременно в нуль; через каждую обыкновенную точку проходит одна фазовая траектория. Точка 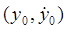называется особой точкой, есл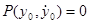и и .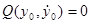

Замечание. Особые точки классифицируются по характеру фазовых траекторий в их окрестности.

Исследование на устойчивость некоторого решения 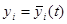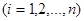системы (24.1) можно свести к исследованию тривиального решения – точки покоя, расположенной в начале координат, преобразуя систему к новым переменным: 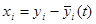- отклонениям прежних неизвестных от решения, исследуемого на устойчивость. В новых переменных система (24.1) принимает вид:

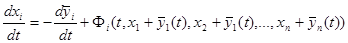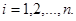, (24.8)

Простейшие типы точек покоя.

Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:

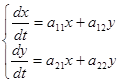, где 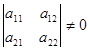. (24.9)

Характеристическое уравнение при этом имеет вид:

.

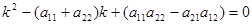Рассмотрим различные наборы корней этого уравнения:

1) k₁ и k₂ действительны и различны. Тогда общее решение системы (24.9) можно задать так: 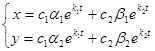. При этом возможны следующие случаи:

а) если k₁ < 0 и k₂ < 0, то точка покоя асимптотически устойчива, так как 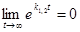, и все точки, находящиеся в начальный момент t = t₀ в любой δ – окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой ε – окрестности начала координат, а при 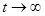стремятся к началу координат. Такая точка покоя называется устойчивым узлом.

б) если k₁ > 0, k₂ >0, можно свести исследование к предыдущему случаю заменой t на –t. При этом фазовые траектории имеют такой же вид, но направление движения меняется на противоположное, то есть при увеличении t точка удаляется от начала координат, поэтому подобная точка покоя – неустойчивый узел – неустойчива по Ляпунову.

в) при k₁ > 0, k₂ < 0 точка покоя тоже неустойчива, так как движущаяся по траектории

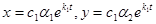точка с возрастанием t выходит из ε – окрестности начала координат. Точка покоя рассматриваемого типа называется седлом.

2) k_1,2 = p ± qi . Тогда общее решение системы (24.9) можно представить в ви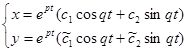де

, где 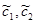- линейные комбинации произвольных постоянных с₁, с₂. При этом возможны следующие случаи:

а) p < 0, q ≠ 0. Тогда 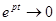при 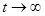, а тригонометрические функции являются ограниченными. Поэтому фазовые траектории являются спиралями, асимптотически приближающимися при 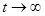к началу координат. Таким образом, точка покоя асимптотически устойчива. Она называется устойчивым фокусом.

б) p > 0, q ≠ 0. Изменяется направление движения по фазовым траекториям, следовательно, точки удаляются от начала координат и точка покоя неустойчива – неустойчивый фокус.

в) р = 0. Траекториями являются замкнутые кривые, окружающие точку покоя, называемую в этом случае центром. Такая точка покоя устойчива, так как можно подобрать такое δ, что замкнутые траектории, начальные точки которых лежат в δ – окрестности начала координат, не выходят за пределы ε – окрестности начала координат (x² (t) + y² (t) < ε² ).

3) Корни кратны: k₁ = k₂.

а) k₁ = k₂ < 0. Тогда общее решение 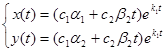стремится к нулю при 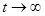, и точка покоя вновь называется устойчивым узлом. При 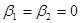получаем частный случай устойчивого узла – так называемый дикритический узел.

б) k₁ = k₂ > 0. Направление движения по траекториям меняется - неустойчивый узел.