Метод последовательных разностей, метод отклонений уровня ряда от основной тенденции, метод включения фактора времени
Метод отклонений от тренда:
Имеются 2 временных ряда х1 и у1, каждый из которых содержит трендовую компоненту Т и случайную компоненту Ɛ. Аналитическое выравнивание каждого из этих рядов позволяет найти параметры соответсвующих уравнений трендов и определить расчетные по тренду уровни 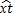 и
и 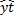 соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты Т каждого ряда. Поэтому влияние тенденций можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда
соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты Т каждого ряда. Поэтому влияние тенденций можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда 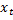 -
- 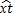 и
и 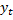 -
- 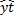 при условии, что последние не содержат тенденции.
при условии, что последние не содержат тенденции.
Временные ряды отклонений от трендов можно использовать для получения количественной характеристики тесноты связи исходных временных рядов расходов на конечное потребление и общего дохода (например). Содержательная интерпретация параметров этой модели затруднительна, однако ее можно использовать для прогнозирования. Для этого необходимо определить трендовое значение факторного признака 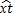 и с помощью одного из методов оценить величину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного признака определяют трендовое значение
и с помощью одного из методов оценить величину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного признака определяют трендовое значение 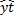 , а по уравнению регрессии по отклонениям от трендов находят величину отклонения
, а по уравнению регрессии по отклонениям от трендов находят величину отклонения 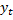 -
- 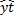 . Затем рассчитывают точечный прогноз фактического значения
. Затем рассчитывают точечный прогноз фактического значения 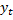 по формуле:
по формуле: 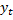 =
= 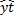 + (
+ ( 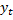 -
- 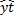 ).
).
Метод последовательных разностей:
В ряде случаев вместо аналитического выравнивания временного ряда с целью устранения тенденции можно применить более простой метод – метод последовательных разностей. Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами (первыми разностями).
Пусть 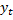 =
= 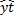 +
+ 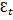 , (1) где
, (1) где 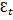 - случайная ошибка.
- случайная ошибка. 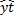 = a + b * t. (2) Тогда
= a + b * t. (2) Тогда 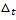 =
= 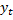 -
- 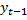 = a + b*t +
= a + b*t + 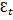 - (a + b*(t – 1) +
- (a + b*(t – 1) + 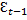 ) = b + (
) = b + ( 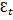 -
- 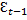 ). (3)
). (3)
Коэфф-нт b - константа, которая не зависит от времен. При наличии сильной линейной тенденции остатки 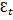 достаточно малы в соответствии с предпосылками МНК носят случайный характер. Поэтому первые разности уровней ряда
достаточно малы в соответствии с предпосылками МНК носят случайный характер. Поэтому первые разности уровней ряда 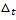 не зависят от переменной времени, их можно использовать для дальнейшего анализа.
не зависят от переменной времени, их можно использовать для дальнейшего анализа.
Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности. Пусть имеет место соотношение (1), однако
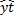 = a +
= a + 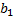 * t +
* t + 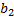 *
* 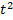 (4).Тогда
(4).Тогда 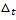 =
= 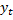 -
- 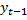 = a +
= a + 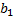 *t +
*t + 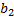 *
* 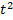 +
+ 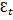 - (a -
- (a - 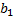 * (t - 1) +
* (t - 1) + 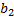 *
* 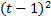 +
+ 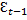 ) =
) = 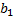 -
- 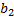 + 2*
+ 2* 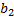 *t + (
*t + ( 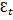 -
- 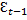 ). (5)
). (5)
Как показывает это соотношение, первые разности 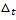 непосредственно зависят от фактора времени t и, следовательно, содержат тенденцию. Определим вторые разности:
непосредственно зависят от фактора времени t и, следовательно, содержат тенденцию. Определим вторые разности:
2 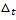 =
= 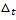 -
- 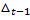 =
= 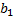 -
- 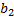 + 2*
+ 2* 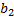 *t + (
*t + ( 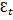 -
- 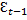 ) –(
) –( 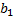 -
- 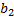 + 2*
+ 2* 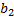 *(t – 1) + (
*(t – 1) + ( 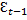 -
- 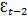 )) = 2*
)) = 2* 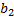 + (
+ ( 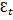 - 2*
- 2* 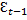 +
+ 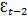 ) (6).
) (6).
Очевидно, что вторые разности не содержат тенденции, поэтому при наличии в исходных уровнях тренда в форме параболы второго порядка их можно использовать для дальнейшего анализа. Если тенденции временного ряда соответствуют экспоненциальный, или степенной, тренд, метод последовательных разностей следует применить не к исходным уровням ряда, а к их логарифмам.
Включение в модель регрессии фактора времени:
В корреляционно-регрессионном анализе можно устранить воздействие какого-либо фактора, если зафиксировать воздействие этого фактора на результат и другие включенные в модель факторы. Данный прием широко применяется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной. Модель вида 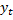 = a +
= a + 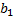 *
* 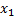 +
+ 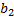 *t +
*t + 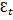 (7) относится к группе моделей, включающих фактор времени. Очевидно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только текущие , но и лаговые значения независимой и результативной переменных.
(7) относится к группе моделей, включающих фактор времени. Очевидно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только текущие , но и лаговые значения независимой и результативной переменных.
Преимущество данной модели перед методами отклонений от трендов и последовательных разностей состоит в том, что она позволяет учесть всю информацию, содержащуюся в исходных данных, поскольку значения 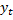 и
и 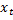 - это уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры a и b модели с включением фактора времени определяются обычным МНК.
- это уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры a и b модели с включением фактора времени определяются обычным МНК.
