Типовые задачи, используемые при формировании
вариантов текущего контроля
Модуль1. Интегральное исчисление функций одной переменной
Контрольная работа №1 «Техника интегрирования»
Найти неопределенные интегралы:
1. 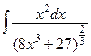 2.
2. 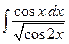 3.
3. 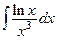 4.
4. 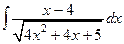 5.
5. 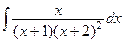
6. 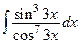 7.
7. 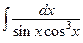 8.
8. 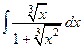 9.
9. 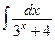 10.
10. 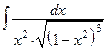
Домашнее задание №1 «Приложения определенного интеграла.
1. Вычислить площадь фигуры, которая расположена на плоскости Oxy и ограничена линиями 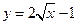 ,
, 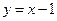 .
.
2. Фигура, расположенная на плоскости XОY, и ограниченная линиями 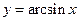 ,
, 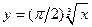 вращается вокруг оси. OY. Вычислить объём полученного тела вращения..
вращается вокруг оси. OY. Вычислить объём полученного тела вращения..
3. Вычислить площадь фигуры., расположенной внутри кривой 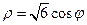 и одновременно вне кривой
и одновременно вне кривой 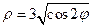 .
.
4. Вычислить длину дуги кривой 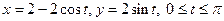 .
.
5. Вычислить площадь поверхности, полученной при вращении линии 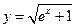 вокруг
вокруг
оси ОХ.
6. Исследовать несобственные интегралы на сходимость.
а) 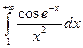 , б)
, б) 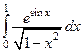 .
.
Рубежный контроль №1 «Приложения определенного интеграла».
1. Дать определение первообразной и сформулировать теоремы о первообразных.
2. Исследовать на сходимость и вычислить (если это возможно):
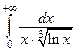
3. Найти площадь фигуры, расположенной внутри кривой 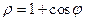 и вне кривой
и вне кривой 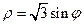 .
.
4. Найти объём тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 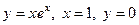 .
.
5. Найти площадь поверхности, образованной вращением вокруг оси ОY области, ограниченной линиями 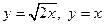 .
.
Модуль 2. Дифференциальные уравнения.
Контрольная работа №2 «Дифференциальные уравнения первого порядка»
1. Решить задачу Коши 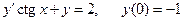
2. Найти общее решение ДУ 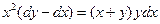
3. Найти общее решение ДУ 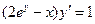
4. Решить задачу Коши 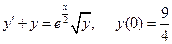
5. Найти общее решение ДУ 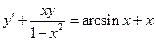
Домашнее задание №2 “Дифференциальные уравнения высшего порядка”
1. Найти общее решение дифференциального уравнения.
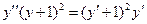
2. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
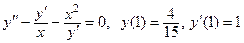
3. Найти общее решение дифференциального уравнения.
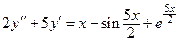
4. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
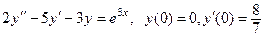
5. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка, если известно одно частное решение 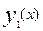 соответствующего однородного уравнения
соответствующего однородного уравнения
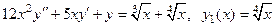
6. Методом изоклин найти приближенное решение дифференциального уравнения первого порядка
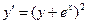
Рубежный контроль№2 “Дифференциальные уравнения высшего порядка”
Типовые задачи
1.ДУ 1-го порядка, интегральные кривые, задача Коши, частное и общее решение, частный и общий интеграл, теорема существования и единственности решения задачи Коши.
2. Найти общее решение ДУ
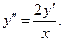
3. Найти решение задачи Коши
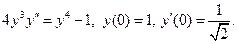
4. Найти общее решение ДУ
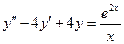
5. Найти общее решение ДУ
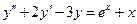
Вопросы для подготовки к контролям по модулям и экзамену
Модуль 1. Интегральное исчисление функций одной переменной
1. Первообразная. Доказать теоремы о первообразных. Неопределенный
интеграл и его свойства. Таблица неопределенных интегралов, ее вывод.
2. Интегрирование подстановкой и по частям – вывод. Примеры. Интегрирование выражений, содержащих квадратный трехчлен в знаменателе. Интегрирование тригонометрических и иррациональных функций.
3. Разложение правильной рациональной дроби в сумму простейших. Примеры. Интегрирование простейших дробей. Интегрирование неправильных рациональных дробей.
4. Определенный интеграл, его механический и геометрический смысл, теорема существования. Доказать линейность определенного интеграла и вывести формулу для определенного интеграла от константы.
5. Доказать теоремы о переходе в неравенстве к интегралам, об оценке и о среднем для определенного интеграла.
6. Определенный интеграл с переменным верхним пределом. Доказать теорему о производной интеграла с переменным верхним пределом. Вывести формулу Ньютона-Лейбница.
7. Вычисление определенного интеграла подстановкой и по частям (вывод). Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат (вывод), интегрирование периодических функций. Примеры.
8. Несобственные интегралы 1-го и2-го рода, доказать их свойства. Признаки сходимости. Примеры. Абсолютная и условная сходимость несобственных интегралов. Доказать теорему о связи абсолютной сходимости и обычной. Примеры.
9.Вычисление площадей плоских фигур в декартовых и полярных координатах (вывод).
10. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения (вывод).
11. Вычисление длины дуги кривой и площади поверхности вращения (вывод).
Модуль 2 Дифференциальные уравнения
12. Дифференциальные уравнения (ДУ_ 1-го порядка). Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ. Примеры.
13. Геометрическая интерпретация ДУ 1-го порядка. Поле направлений. Геометрическое решение ДУ 1-го порядка с помощью изоклин. Примеры.
14. Простейшие типы ДУ 1-го порядка (с разделяющимися переменными, однородные, линейные, Бернулли) и их решение. Примеры.
15. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при 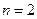 . Теорема существования и единственности решения задачи Коши. Краевая задача.
. Теорема существования и единственности решения задачи Коши. Краевая задача.
16. Понижение порядка некоторых типов ДУ высших порядков.
17. Линейные ДУ (ЛДУ) п-го порядка: однородные (ОЛДУ) и неоднородные. Теорема о существовании и единственности решения. Линейный дифференциальный оператор. Доказать свойства линейного дифференциального оператора и линейность пространства решений ОЛДУ.
18. Линейная зависимость функций. Определитель Вронского (вронскиан). Доказать теорему о вронскиане системы линейно зависимых функций и теорему о вронскиане системы линейно независимых частных решений ОЛДУ.
19. Доказать теорему о размерности пространства решений ОЛДУ n-го порядка. Фундаментальная система решений. Структура общего решения.
20. Формула Остроградского-Лиувилля для ОЛДУ n-го порядка (вывод для 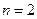 ) и ее следствия.
) и ее следствия.
21. Доказать теорему о структуре общего решения неоднородного ЛДУ n-го порядка и теорему о наложении частных решений.
22 ОЛДУ с постоянными коэффициентами. Характеристическое уравнение и построение общего решения по его корням (вывод для 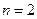 ).
).
23. Нахождение частных решений неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида.
24. Метод вариации постоянных решения неоднородных ЛДУ n-го порядка (вывод для 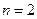 ).
).
25. Нормальные системы ДУ. Задача Коши и теорема о существовании и единственности ее решения. Сведение ДУ n-го порядка к нормальной системе, примеры. Сведение нормальной системы к одному уравнению n-го порядка (вывод для 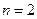 ), примеры.
), примеры.
26. Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов. Примеры.
27. Системы ЛДУ 1-го порядка, однородные и неоднородные. Матричная запись системы. Доказать линейность пространства решений системы ОЛДУ.
28. Вронскиан системы векторных функций и его свойства. Доказать теорему о размерности пространства решений системы ОЛДУ. Структура общего решения . Фундаментальная система решений.
29. Структура общего решения системы неоднородных ЛДУ. Метод вариации произвольных постоянных (вывод).
30. Системы ОЛДУ с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения по корням характеристического уравнения (вывод для случая вещественных различных корней).
Модуль 3. Итоговый контроль (экзамен)
Формулировки определений, свойств и теорем, перечисленных выше в п. 1 – 30.
Иллюстрация всех теоретических положений примерами.
Теоремы с изложением доказательства:
1. Доказательство теорем об общем виде первообразной данной функции и о ее свойствах.
2. Доказательство правила подведения под знак дифференциала, замены переменной и интегрирования по частям для неопределенного интеграла.
3. Доказательство правила подведения под знак дифференциала, замены переменной и интегрирования по частям для определенного интеграла
4. Доказательство свойств линейности определенного интеграла. Вычисление определенного интеграла от константы.
5. Доказательство теорем о переходе к интегралам в неравенстве, об оценке и о среднем для определенного интеграла.
6. Доказательство теоремы о производной интеграла с переменным верхним пределом и формулы Ньютона - Лейбница.
7. Вывод формулы для площади плоской фигуры в декартовых и полярных координатах
8. Вывод формулы для объема тела по площадям поперечных сечений и объемов тел вращения.
9. Вывод формул для длины дуги кривой и площади поверхности вращения.
10. Доказательство свойств несобственных интегралов.
11. Доказательство теоремы о связи абсолютной и условной сходимости несобственного интеграла.
12. Доказательство свойства линейности дифференциального оператора однородного линейного дифференциального уравнения (ОЛДУ) n-го порядка и линейность пространства решений ОЛДУ.
11. Доказательство теоремы о вронскиане системы линейно зависимых функций и теоремы о вронскиане системы линейно независимых частных решений ОЛДУ.
12. Доказательство теоремы о размерности пространства решений ОЛДУ n-го порядка и теоремы о структуре общего решения ОЛДУ.
13. Вывод формулы Остроградского-Лиувилля для ОЛДУ второго порядка и доказательство следствия из нее.
14. Доказательство теоремы о структуре общего решения неоднородного ЛДУ n-го порядка и теоремы о наложении частных решений.
15. Вывод характеристического уравнения для ОЛДУ n-го порядка с постоянными коэффициентами. Вывод способа построения фундаментальной системы решений ОЛДУ с постоянными коэффициентами при 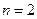 .
.
16. Доказательство теоремы о решении неоднородных ЛДУ n-го порядка (для 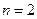 )
)
методом вариации произвольных постоянных.
17. Доказательство теоремы о сведении ДУ n-го порядка к нормальной системе ДУ и о сведении нормальной системы двух ДУ к одному ДУ 2-го порядка.
18. Доказательство линейности пространства решений системы ОЛДУ.
19. Доказательство теоремы о размерности пространства решений системы ОЛДУ и о структуре общего решения системы ОЛДУ.
20. Доказательство теоремы о решении системы неоднородных ЛДУ методом вариации произвольных постоянных.
21. Доказательство теоремы о построении общего решения по корням характеристического уравнения системы ОЛДУ с постоянными коэффициентами в случае вещественных различных корней.
