Исправленный метод Эйлера решения задачи Коши для ОДУ 1 порядка

В усовершенствованном методе Эйлера усреднялись наклоны касательных, т.е. производные от искомой функции. В модифицированном методе происходит усреднение точек (рис.7.8).

Прямая L₁ есть касательная к истинной кривой y=y(x) в точке (x_m, y_m). Ее наклон к оси OX равен углу 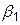, для которого

,

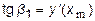или в силу (7.2):

.

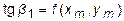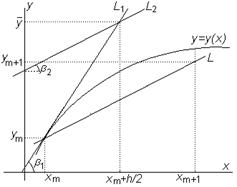
Рис.7.8. Модифицированный метод Эйлера

Прямая L₂ есть касательная к решению уравнения (7.2) в точке 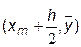, являющей­ся пересечением L₁ c прямой x = x_m+h/2. Наклон L₂ равен углу 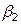, для которого

.

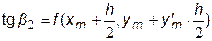Прямая L параллельна прямой L₂ и проходит через точку (x_m, y_m), а ее пересечение c пря­мой x = x_m+1 и определяет окончательное значение y_m+1 решения уравнения в тоске x_m+1. Уравнение прямой L можно записать в виде

,

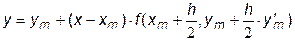где .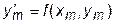

Поэтому

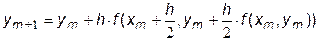(7.12)

Выражение (7.12) есть вычислительная формула модифицированного метода Эйлера.

Он также согласуется с разложением в ряд Тейлора с точностью до h². Блок-схема этого алгоритма аналогична предыдущей и отличается лишь формулой в блоке «ордината следующей точки».