Методы решения систем линейных уравнений

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Институт цветных металлов и золота СФУ»

Н.А.Братухина

Т.П. Бугаева

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

КОМПЛЕКСНЫЕ ЧИСЛА

Методические указания для выполнения контрольной работы №2 студентов заочной формы обучения всех специальностей

Красноярск 2007

Системы линейных алгебраических уравнений. Комплексные числа / Н.А.Братухина, Т.П. Бугаева; ГОУ ВПО «Институт цветных металлов и золота СФУ».- Красноярск, 2007.- с.

Методические указания включают в себя разделы, изучаемые студентами заочной формы обучения в рамках первой контрольной работы. При изучении данной работы студентам предлагается краткая теория, решение базовых заданий, вопросы для самоконтроля, необходимых для выполнения контрольной работы и сдачи экзамена по предложенным разделам.

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Основные понятия и определения

Рассмотрим систему m линейных алгебраических уравнений с n неизвестными

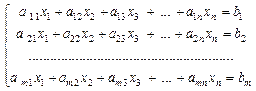, (1)

где x₁, x₂, x₃, …, x_n – неизвестные системы уравнений, b₁, b₂, …, b_m- свободные члены, a_ij ( 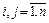) – коэффициенты при неизвестных.

Матрицу, состоящую из коэффициентов при неизвестных

,

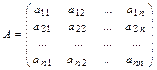называют основной матрицей системы.

Основная матрица системы, в которую включили столбец свободных членов

,

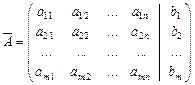называется расширенной матрицей системы.

Рангом матрицы системы (1) называют наивысший порядок отличного от нуля минора.

Система линейных алгебраических уравнений (1) называется неоднородной, если среди свободных членов b_i найдется хотя бы одно, отличное от нуля значение.

Система линейных алгебраических уравнений (1) называется однородной, если все b_i равны нулю:

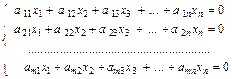. (2)

Решить систему уравнений – значит найти все значения неизвестных x_i, при подстановке которых в выражение (1), каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если имеет одно или множество решений.

Система уравнений не имеющая решений называется несовместной.

Однородная система уравнений (2) всегда совместна.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же решение.

Эквивалентные системы получаются в результате элементарных преобразований над матрицами.

Элементарными преобразованиями матриц являются:

· перестановка местами двух строк (столбиков) матрицы;

· умножение всех элементов строки матрицы на число, отличное отнуля;

· суммирование элементов строки матрицы с соответствующими элементами другой строки, умноженной на одно и то же число;

· вычеркивание нулевой строки матрицы.

Методы решения систем линейных уравнений

Основными методами решения систем линейных уравнений являются

· метод Крамера;

· матричный метод;

· метод Гаусса.

Выбор методов решения систем уравнений зависит от количества уравнений в системе и количества неизвестных.

Если число уравнений равно числу неизвестных, то для решения систем применяют метод Крамера или матричный метод.

Метод Гаусса используют для решения систем с произвольным числом уравнений и неизвестных.

Метод Крамера

Данный метод применяют для решения, так называемых, квадратных систем (число уравнений системы равно числу неизвестных):

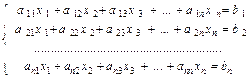, (3)

главный определитель Δ которoй отличен от нуля

.

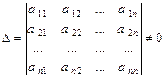Решение системы (3) находят по формулам Крамера:

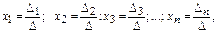
где 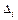- это вспомогательные определители системы, полученные путем замены i – того столбика главного определителя, столбцом свободных членов:

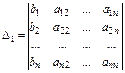- первый вспомогательный определитель,

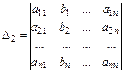- второй вспомогательный определитель,

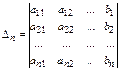- n – ый вспомогательный определитель.

Замечание. Если главный определитель системы отличен от нуля D ¹ 0, то система имеет единственное решение.

Если главный определитель системы равен нулю D = 0 и все вспомогательные определители равны нулю D_i= 0, то система имеет множество решений.

Если главный определитель системы равен нулю D = 0 , а среди вспомогательных определителей найдется хотя бы один отличный от нуля, то система решений не имеет.

Пример 1. Решить систему уравнений методом Крамера

.

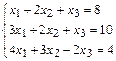Решение. Вычислим главный определитель системы D, элементами которого являются коэффициенты при неизвестных:

.

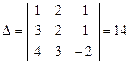Далее найдем значения вспомогательных определителей D₁, D_2, D₃.

Первый вспомогательный определитель D₁ получим заменой первого столбика главного определителя D свободными членами:

.

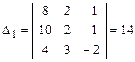Второй вспомогательный определитель D₂ получим заменой второго столбика главного определителя D свободными членами:

.

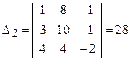Третий вспомогательный определитель D₃ получим заменой третьего столбика главного определителя D свободными членами:

.

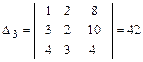Неизвестные члены x_i системы уравнений вычислим по формулам Крамера:

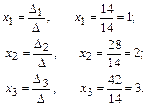
Ответ.(1; 2; 3).

Матричный метод

Данный метод применяется для решения систем линейных алгебраических уравнений, содержащих n уравнений с n неизвестными

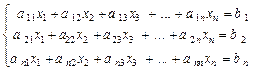, (4)

если определитель основной матрицы системы отличен от нуля D ¹ 0.