Перед тем как перейти к приложениям теории групп, рассмотрим более детально понятие представления. Мы не будем излагать абстрактные методы определения представлений, поскольку достаточно полное изложение теории представлений является предметом отдельного курса и поскольку для всех точечных групп имеются таблицы неприводимых представлений (таблицы характеров). Мы приводим здесь краткое изложение представлений, неприводимых представлений, также некоторых других понятий, необходимых для практического применения теории представлений. Примем без доказательства три свойства неприводимых представлений:
1. Если неприводимые представления группы одномерны, то они сами образуют группу
2. Сумма квадратов размерностей неприводимых представлений равна порядку группы.
3. Число различных неприводимых представлений группы равно числу его классов.
Рассмотрим операции Е и С2 точечной группы С2. Соответствующие им трёхмерные матрицы преобразований имеют вид
R(E) = 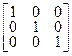 | (4.1) |
R(C2) = 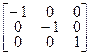 | (4.2) |
Эти матрицы дают представление группы С2. Однако оно не является самым простым. Это представление задаётся диагональными матрицами преобразований в декартовой системе координат. Следовательно, x-, y- и z-компоненты единичного вектора преобразуются независимо друг от друга. Рассматривая эти компоненты, мы получаем три независимых отображения нашей группы Г(x), Г(y), Г(z):
| | Е | С2 | (4.3) |
| Г(x) | | -1 |
| Г(y) | | -1 |
| Г(z) | | |
В силу ортогональности базисных векторов декартовой системы координат эти отображения взаимно независимы. Отметим, что Г(z ) – гомоморфизм для элементов из С2, тогда как Г(x) и Г(y) – изоморфизмы). В отдельности их можно рассматривать как представления точечной группы С2. Числа, выражающие эти представления, называются характерами. (Вообще говоря, характер – это след матрицы, представляющей данную операцию данной группы. В данном случае независимые матрицы одномерны). Однако, в силу того что Г(x) совпадает с Г(y), они дают одинаковую информацию об элементах группы С2. Поэтому Г(z) и Г(x) (или Г(y)) дают два единственных одномерных представления группы С2 в декартовой системе координат. Они называются неприводимыми представлениями. Таблица характеров для группы включает характеры для различных операций, связанных с каждым неприводимым представлением. Таблица характеров для С2 имеет вид
Неприводимые представления являются простейшим возможным множеством независимых матриц, дающих представление группы. Ниже мы обсудим смысл обозначений А и В для неприводимых представлений.
Перейдём теперь к матрицам преобразований для точечной группы С3:
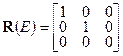 | (4.5) |
R(С3) = 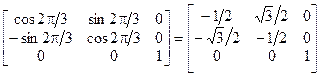 | (4.6) |
R 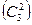 = = 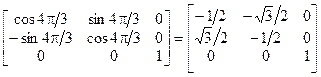 | (4.7) |
Матрицы для С3-операций не являются диагональными; следовательно, x- и y- компоненты нельзя по отдельности использовать для образования неприводимых представлений группы С3. Однако z-компонента и в этом случае порождает одномерное независимое (неприводимое) представление. Квадратные матрицы второго порядка, описывающие преобразование в координатах x и y, можно использовать в качестве двумерного представления точечной группы С3. Это также неприводимое представление. Существуют два способа для выражения такого неприводимого представления. Согласно одному из них, в качестве характеров этого представления используют следы двумерных матриц. Это приводит к следующей таблице характеров:
(Отметим, что характеры в (4.4) рассматриваются как следы одномерных матриц). Второй способ – это диагонализация матриц (4.6) и (4.7) (синус и косинус предварительно выражаются в экспоненциальной форме). В результате получаем
R’(C3) = 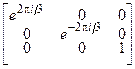 | (4.9) |
R’ 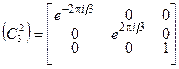 | (4.10) |
Два первых диагональных элемента полученных матриц всё ещё не являются взаимно независимыми, поскольку они комплексно сопряжены друг с другом. Однако это позволяет нам разложить двумерное представление на два мнимых одномерных представления:
Как (4.8), так и (4.11) являются таблицами характеров точечной группы С3. Обе таблицы показывают, что эта группа может быть представлена одним одномерным и одним двумерным неприводимыми представлениями. Мнимая форма обычно приводится в таблицах характеров циклических групп, а действительная используется в том случае, когда имеются дополнительные генераторы. Данный пример выбран нами для того, чтобы получить надлежащие соотношения между размерностями представлений и порядком группы.
Перейдём к рассмотрения точечной группы С2v. Её элементы: Е, С2, 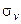 и
и 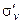 . Их трёхмерные матрицы в случае, когда ось z – ось поворота, плоскость xz - σv, yz -
. Их трёхмерные матрицы в случае, когда ось z – ось поворота, плоскость xz - σv, yz - 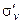 , имеют вид
, имеют вид
 R(Е) = R(Е) = 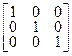 | (4.12) |
R(С2) = 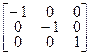 | (4.13) |
R 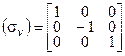 | (4.14) |
R 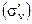 = = 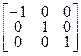 | (4.15) |
Эти матрицы диагональные; следовательно, мы сразу можем написать три одномерных представления:
| С2v | E | C2 | σv | 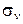 | (4.16) |
| Г(x) | | -1 | | -1 |
| Г(y) | | -1 | -1 | |
| Г(z) | | | | |
Однако это ещё не все неприводимые представления данной точечной группы. Одномерные неприводимые представления сами образуют группу, если произведение определить следующим образом:
| Г(а) × Г(b) = Г(с), | (4.17а) |
где
и аi, bi и ci представляют характеры данного элемента в неприводимых представлениях Г(а), Г(b) и Г(с) соответственно. Итак в случае трёх представлений точечной группы С2v имеем
| Г(z) × Г(x) = | 1×1 | 1×(-1) | 1×1 | 1×(-1) | (4.18) |
| = | | -1 | | -1 |
| = | Г(x) | | | |
| Г(z) × Г(y) = | 1×1 | 1×(-1) | 1×(-1) | 1×1 | (4.19) |
| = | | -1 | -1 | |
| = | Г(y) | | | |
| Г(x) × Г(y) = | 1×1 | -1×-1 | 1×(-1) | -1×1 | (4.20) |
| = | | | -1 | -1 |
Соотношения (4.18) и (4.19) удовлетворяют (4.17а) для трёх определённых выше представлений; однако (4.20) даёт новое представление. Это единственно возможные четыре неприводимых представления, которые могут быть построены для точечной группы С2v с помощью введённой нами процедуры. Таблица характеров, следовательно имеет вид
| С2v | Е | С2 | σv | 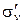 | | (4.21) |
| А1 | | | | |
| А2 | | | -1 | -1 |
| В1 | | -1 | | -1 |
| В2 | | -1 | -1 | |
Точечная группа С2 имеет два элемента симметрии. Она также обладает двумя одномерными неприводимыми представлениями, которые можно определить из поведения её элементов по отношению к двумерному пространству. Точечная группа С3 имеет три элемента симметрии. В таблице характеров этой группы содержится одно одномерное и одно двумерное представления, полученные в трёхмерном пространстве. Точечная группа С2v имеет четыре элемента симметрии. Её таблица характеров состоит из четырёх одномерных неприводимых представлений. Если задано четырёхмерное пространство, в котором матрицы элементов точечной группы С2v имеют вид (4.22 – 4.25), то складывается ситуация (аналогичная случаю С2), в которой неприводимые представления можно определить просто из рассмотрения поведения элементов матричных представлений элементов симметрии по отношению к каждому из базисных векторов четырехмерного пространства. Такую же процедуру получения представлений можно применить к любой точечной группе.
R(E) = 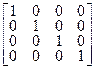 | (4.22) |
R(С2) = 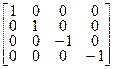 | (4.23) |
R(σv) = 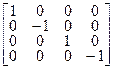 | (4.24) |
R( 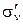 ) = ) = 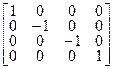 | (4.25) |
Если задано n элементов симметрии, то можно построить n- мерное пространство, с помощью которого затем определяются неприводимые представления на основе анализа поведения матричных элементов матриц представлений элементов симметрии в n-мерном пространстве.[3]
Для аксиальных точечных групп все неприводимые представления либо одномерны, либо двумерны. Двумерные представления присущи всем циклическим группам с порядком оси поворота выше второго. Добавим, что кубические точечные группы обладают трехмерными неприводимыми представлениями, а группы, основанные на более высоких правильных многогранниках, имеют неприводимые представления более высокой размерности.
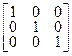
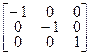
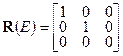
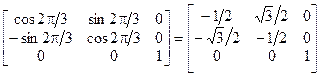
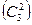 =
= 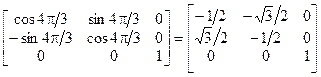
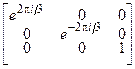
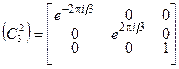
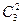
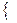
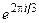
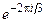
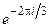
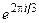
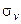 и
и 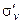 . Их трёхмерные матрицы в случае, когда ось z – ось поворота, плоскость xz - σv, yz -
. Их трёхмерные матрицы в случае, когда ось z – ось поворота, плоскость xz - σv, yz - 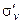 , имеют вид
, имеют вид R(Е) =
R(Е) = 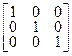
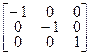
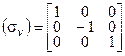
 =
= 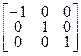
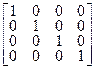
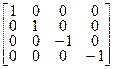
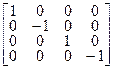
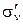 ) =
) =