Неприводимые многочлены в конечном поле K

В этом разделе мы научимся определять для заданного многочлена 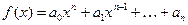с коэффициентами из конечного поля P={0, 1, 2, ... q - 1}, является ли этот многочлен неприводимым в поле P. Неприводимые многочлены используются для построения линейных сдвиговых регистров с обратной связью (см. раздел 3.1.6). Наш алгоритм основывается на следующей теореме.

Теорема. Пусть F – конечное поле, состоящее из q элементов. Тогда для любого натурального 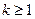многочлен 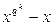является произведением всех неприводимых над полем F многочленов степени k.

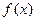
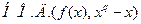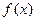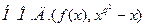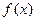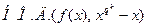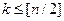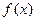Из этой теоремы сразу следует, что для произвольного многочлена является произведением всех линейных сомножителей , является произведением всех квадратичных сомножителей и т.д. Поэтому, если =1 для , то является неприводимым многочленом. Наибольший общий делитель двух многочленов находят с помощью алгоритма Евклида, используя соотношени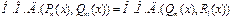е , где 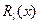- остаток от деления 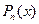на .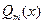

Упомянутый тест на неприводимость можно заменить более быстрым альтернативным тестом: многочлен 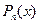над полем F= 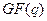является неприводимым тогда и только тогда, когда 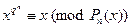, и 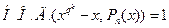для всех простых делителей k степени n.

Пример. Показать неразложимость многочлена 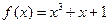над полем F₂={0,1}.

В данном случае, n=3, q=2. Для вычисления 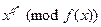поделим столбиком 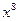на 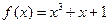и найдем остаток: . Остаток равен x. Простым делителям числа n=3 являются только k=1, поэтому остается только проверить, что 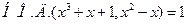. Для этого делим первый многочлен на второй и находим остаток 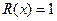. Теперь по алгоритму Евклида .

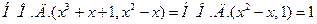14. ρ-метод Полларда для дискретного логарифмирования — алгоритм дискретного логарифмирования в кольце вычетов по простому модулю, имеющий экспоненциальную сложность. Он был предложен Поллардом в 1978 году.

Постановка задачи

Для заданного простого числа p и двух целых чисел a и b требуется найти целое число x, удовлетворяющее сравнению: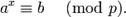

Идея алгоритма

Рассматриваются три числовые последовательности: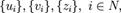

определённые следующим образом: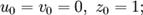

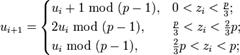
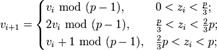
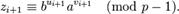
Замечание: везде рассматривается наименьшие неотрицательные вычеты.

Далее рассматриваются наборы 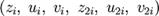и ищется номер i, для которого 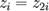. Для такого i выполнено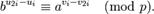

Если при этом 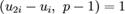, то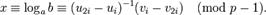

Эвристическая оценка сложности составляет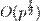

15. Методы факторизации целых чисел. (ρ-1) – метод Полларда.

Факторизацией целого числа называется его разложение в

произведение простых сомножителей. Такое разложение, согласно основной

теореме арифметики, всегда существует и является единственным (с

точностью до порядка следования множителей). Задача факторизации является вычислительно сложной задачей. Однако никому пока не удалось получить высоких нижних оценок этого алгоритма.

Все методы факторизации в зависимости от их производительности можно разбить на две группы: экспоненциальные методы и субэкспоненциальные методы. Среди субэкспоненциальных алгоритмов следует выделить метод эллиптических кривых Ленстры, являющийся аналогом (ρ − 1)-метода Полларда. Последний имеет экспоненциальную оценку сходимости.

(ρ -1) – метод Полларда основан на Теореме Ферма:

Пусть n—факторизуемое число, а 1 < p < n– его простой делитель. Согласно теореме, для любого a, 1 ≤ a < p, выполняется условие a^p−1 ≡ 1( mod p), если р – простое.

n = p*q, где p,q – нечётные простые числа =>

для любого а<p: a^p-1 mod p = 1, a^q-1 mod q = 1 =>

a^p-1 = k*p, а (p-1) – чётное число.

НОД(a^p-1-1,n) = p.

Предположим: p-1 = 2^{r^1} * 3^{r^2} *…*B^{r^t}. Пусть B<B₁ – грань для множества (p-1).

Вычисляем M(B₁) = ∏ p_i^{r^i}, p_i^{r^i} < B₁.

Выберем произвольное число a, например 2, и вычислим a^M mod n.

Если НОД(n, a^M−1) = d, 1<d<n, то задание выполнено.

Вторая стадия (ρ -1) – алгоритма Полларда.

Вторая стадия алгоритма предполагает, что существует только один

простой множитель q числа p − 1, значение которого больше границы B₁ .

Выбираем новую границу B₂ ~ B₁².

Обозначим через b число a^M(B1) mod n, вычисленное на первой стадии работы алгоритма.

Выпишем последовательность q₀ < q₁ < ... < q_s всех простых чисел на интервале [B₁; B₂] . Если искомый множитель p−1 равен q_i , то для нахождения делителя n, необходимо вычислить c_о = b^qо mod n, и найти d=НОД(n, с_о − 1). Если d = 1, то вычислим следующее c_i. Каждое последующее значение c_i+1 вычисляется по формуле b^qi+1 mod n = b^qi+δi mod n = b^qi · b^δi mod n = c_i · b^δi mod n, где δ_i = q_i+1 − q_i.