Дифференциалы высших порядков

Пусть дифференциал 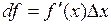функции 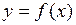в свою очередь является функцией аргумента 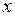. Дифференциал от дифференциала называется дифференциалом второго порядка (или вторым дифференциалом) функции 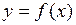в точке 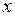и обозначается .

.

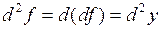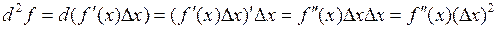Если 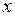- независимая переменная, то 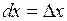, и дифференциал второго порядка примет вид

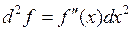или .

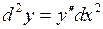Дифференциал от второго дифференциала, если последний есть дифференцируемая функция аргумента 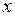, называется дифференциалом третьего порядка (или третьим дифференциалом) данной функции в точке 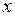и записывается в виде

.

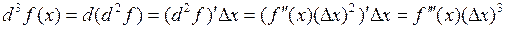Так как 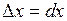для независимой переменной 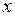, то

.

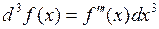Аналогично, дифференциал от дифференциала 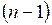-го порядка носит название дифференциала 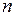-го порядка (или 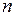-го дифференциала) функции 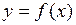в точке 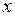и находится по формуле

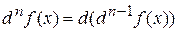
или

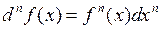(7)

для независимой переменной .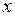

Пример: Найти дифференциал 2-го порядка функции

.

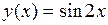Решение: По формуле (7) имеем

.

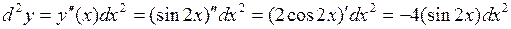Пример: Найти 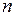-й дифференциал функции

.

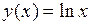Решение: По формуле (7) запишем 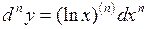. Используя формулу для 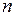-й производной функции 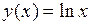, найдем

.

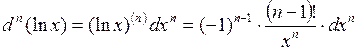Для 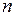-го дифференциала справедливы следующие формулы:

;

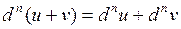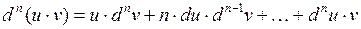- формула Лейбница.

Если функция 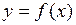имеет конечные производные до 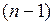-го порядка включительно в некоторой окрестности точки 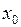и, кроме того, имеет конечную производную 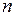-го порядка в самой точке 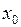, то говорят, что функция 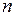раз дифференцируема в точке .

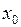Контрольные вопросы:

1. Дайте определение дифференциала функции. Перечислите свойства дифференциала функции. Приведите примеры.

2. Раскройте механический смысл дифференциала.

3. Каким образом дифференциал функции используется в приближенных вычислениях?

4. Как находятся дифференциалы высших порядков?

Литература:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.

2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.

3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.

5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.

6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.