Наивероятнейшее число появления события А в n независимых испытаниях

Наивероятнейшим числом появления события А в n испытаниях называется такое число появлений этого события ( 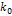), вероятность которого наибольшая.

Наивероятнейшее число появлений 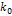события А в n испытаниях можно найти из неравенства:

n•p-q≤ 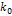≥n•p+p

39. Случайные величины: дискретные и непрерывные. Примеры.

Дискретная с.в.- величина, множество возможных значений которой конечно или счетно.

Закон распределения и функция распределения дискретной случайной величины.

Функция распределения дискретной случайной величины.

Исходной информацией для построения функции распределения дискретной случайной величины X является ряд распределения этой СВ.

xi	x1	x2	x3	...	xn	>xn
pi	p1	p2	p3	...	pn
F(xi)		p1	p1+p2	…	p1+..+pn-1

F(x_i)=P{X<x_i}=P{(X=x₁)È(X=x₂)È ... È(X=x_i-1)}= p₁+...+p_i-1.

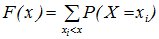, то есть суммирование распространяется на все значения 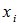, которые меньше х.

Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятности этих значений.

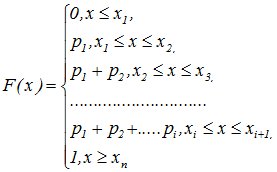(5.5)

Свойства интегральной функции распределения.

Функция распределения и ее свойства.

Наиболее общей формой закона распределения, пригодной для всехслучайных величин (как дискретных, так и недискретных) является функция распределения.

Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x:

F(x)=P{X<x}.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.

1. 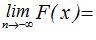F(-¥ ) = 0. (5.2)

2. 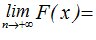F(+¥ ) = 1. (5.3)

3. F(x) – неубывающая функция своего аргумента, т.е. при x₁ < x₂

F(x₁) £ F(x₂).

Доказательство этого свойства иллюстрируется рис. 5.2.

Представим событие C={X<x₂} как сумму двух несовместных событий С=A+B, где A={X<x₁} и B={x₁£X<x₂}.

По правилу сложения вероятностей

P(C)=P(A)+P(B),

т.е. P{X<x₂}=P{X<x₁}+P{x₁£X<x₂}, или

F(x₂)=F(x₁)+P{x₁£X<x₂}.

Но P{x₁£X<x₂}£0, следовательно, F(x₁) £ F(x₂)

4. P(α£ X < β) = F(β) - F(α), для "[α,β[ÎR. (5.4)

Доказательство этого свойства вытекает из предыдущего доказательства.

Вероятность того, что случайная величина Х в результате опыта попадет на участок от α до β (включая α)равна приращению функции распределения на этом участке.

Таким образом, функция распределения F(x)любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0≤F(x)≤1, причем F(-∞)=0, F(+∞)=1.