Примеры. 1. Среднее значение кинетической энергии свободной частицы при температуре T

1. Среднее значение кинетической энергии свободной частицы при температуре T.

Частица трехмерного газа при температуре T, движущаяся поступательно вдоль оси 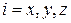, имеет составляющую кинетической энергии

, .

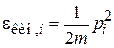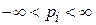Сравниваем с (2.103)

,

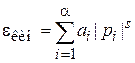находим

, , .

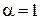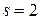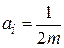Из (2.107)

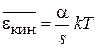
получаем

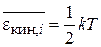. (П.4.1)

Для классического равновесного газа при температуре Т на каждую поступательную степень свободы частицы приходится тепловая кинетическая энергия

.

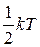2. Энергия линейного гармонического осцилляторапри температуре Т.

Гамильтониан

, ,

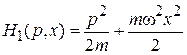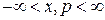сравниваем с (2.108)

,

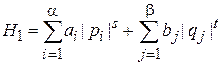получаем

, .

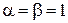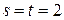Из (2.107)

, ,

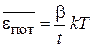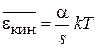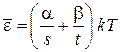
находим

,

,

.

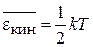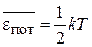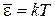На линейное гармоническое колебание при температуре Т приходится тепловая энергия kT, которая складывается из кинетической и потенциальной энергий.

3. Молярная теплоемкость трехмерного, двухмерного и одномерного простого тела при температуре Т.

Простое вещество состоит из атомов одного химического элемента. Кристаллическая трехмерная решетка удерживает атом в узле потенциальным полем. Узел является трехмерным гармоническим осциллятором с гамильтонианом

.

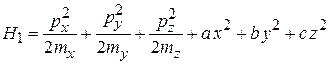Сравнение с (2.103)

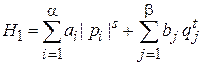
дает

, .

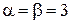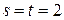Из (2.107) получаем среднюю тепловую энергию атома

.

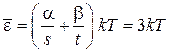Число узлов в моле кристалла равно числу Авогадро 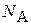. Внутренняя энергия моля

,

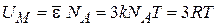где R – универсальная газовая постоянная. Молярная теплоемкость

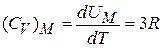. (П.4.2)

Простые твердые тела обладают одинаковой, не зависящей от температуры молярной теплоемкостью – закон Дюлонга и Пти (1819 г.). Закон не применим при низкой температуре и для объектов, где существенны квантовые явления.

Пьер Дюлонг (1785–1838) Алексиз Пти (1791–1820)

Пленка атомарной толщины образует двухмерную кристаллическую решетку, тогда

, , .

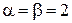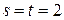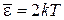Закон Дюлонга и Пти получает вид

.

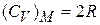Проволока атомарной толщины образует одномерную кристаллическую решетку, тогда

, , .

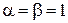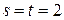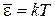Молярная теплоемкость

.

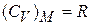4. Флуктуация разности потенциалов в резисторе, вызванная хаотическим тепловым движением.

Колебательный контур содержит резистор R. Внешний сигнал вызывает в контуре колебания. Напряжение с конденсатора С подается на усилитель сигналов У и далее на регистратор в виде осциллографа, как показано на рисунке. Усилитель имеет обратную связь и пропускает колебания с напряжением, превышающим некоторое пороговое значение. Оно является минимальным сигналом, который регистрирует устройство. Для устранения зашумленности полезного сигнала пороговое значение должно превышать величину флуктуации напряжения, вызванную тепловым движением зарядов в резисторе. Найдем эту величину.

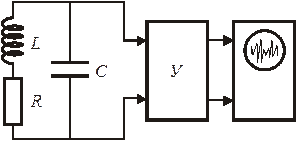
Колебательный контур LCR с усилителем У

Хаотическое движение электронов в резисторе R создает кратковременный ток, конденсатор заряжается, в контуре возникают колебания. Из определения электроемкости 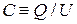получаем связь между среднеквадратичными значениями заряда и напряжения

.

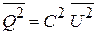Конденсатор рассматриваем как одномерную систему с энергией

, ,

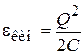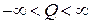где заряд Q аналогичен импульсу. Сравниваем с (2.103)

,

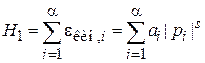находим

, .

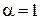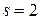Из (2.107)

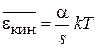
получаем среднюю тепловую энергию колебательного контура

.

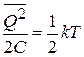Находим

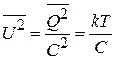
и флуктуацию напряжения

.

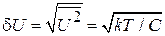Чем выше температура и меньше электроемкость колебательного контура, тем больше флуктуация напряжения на конденсаторе.

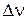Параметры колебательного контура выражаем через ширину частотной полосы пропускания сигнала и реактивное сопротивление X контура

,

.

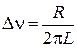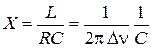Мощность, передаваемая от контура к усилителю, достигает максимумапри согласованной нагрузке, когда входное сопротивление потребителя, то есть усилителя 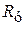, равняется сопротивлению источника X. Получаем

,

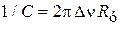тогда

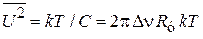
и флуктуация напряжения

.

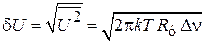Для приемника с полосой пропускания 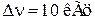, с входным сопротивлением 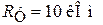и температурой 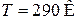получаем флуктуацию напряжения на входе усилителя 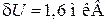, что ограничивает его предельную чувствительность.

Джонсон в 1927 г. подключил резистор к входу усилителя и наблюдал на выходе флуктуацию разности потенциалов. Он обнаружил, что в диапазоне акустических частот дисперсия разности потенциалов теплового шума пропорциональна сопротивлению и температуре резистора

.

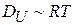Джон Бертранд Джонсон (1887–1970)

5. Флуктуационная ЭДС активного сопротивления.

Электроны в проводнике длиной l образуют идеальный газ. Хаотические тепловые движения газа разлагаем в ряд Фурье. Коллективные перемещения электронов вдоль проводника рассматриваем как стоячие волны смещений газа от равномерного распределения со всеми возможными длинами волн. На концах проводника электроны не выходят за его пределы и возникают узлы смещений. В результате продольные смещения газа имеют дискретный спектр и являются суммой стоячих волн , показанных на рисунке.

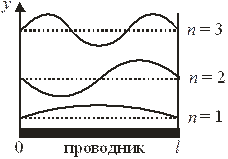
Стоячие волны смещений газа

в проводнике

Смещения электронов создают разность потенциалов на концах проводника. Найдем флуктуацию напряжения, рассматривая волны как линейные гармонические осцилляторы и учитывая, что при температуре T средняя тепловая энергия осциллятора равна .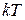

Ищем число волн в интервале частот 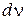. Узлы на концах проводника означают, что на длине проводника l укладывается целое число полуволн 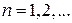, тогда

, ,

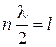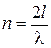где λ – длина волны. Из рис. видно, что n есть число независимых волн в проводнике. C учетом двух проекций спина электрона получаем число волн в интервале частот (0,n)

,

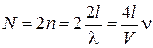где 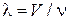; V – скорость волны. Дифференцируем равенство и находим число волн в интервале частот dn

.

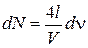Каждая волна является линейным гармоническим осциллятором с тепловой энергией 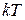, тогда энергия 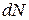волн

.

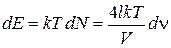Время распространения волны по проводнику 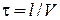, тепловая мощность перемещения электронов

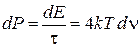
связана с ЭДС законом Джоуля–Ленца

.

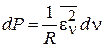Для среднего квадрата фурье-компоненты флуктуационной ЭДС на частоте n получаем формулу Найквиста

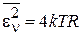. (П.4.4)

Результат установил в 1928 г. Найквист – один из основателей теории информации.

Гарри Найквист (1889–1976)

При 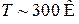ЭДС слабо зависит от частоты и в спектре флуктуаций присутствуют все частоты – флуктуации имеют «белый спектр». Из (П.4.4) находим флуктуацию напряжения на концах проводника

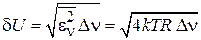, (П.4.5)

где 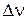– полоса частот, регистрируемая измерителем сигналов. Полученное выражение близко к (П.4.3) из предыдущего примера с колебательным контуром. Формулы (П.4.3) и (П.4.5) применимы, если не существенны квантовые эффекты, то есть при относительно высокой температуре

,

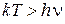где 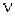– максимальная частота в полосе Dn. При 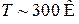получаем 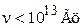. Из (П.4.5) следует, что устройство, имеющее в своей электрической цепи диссипативный элемент – активное сопротивление, является источником теплового электрического шума. При этом чисто реактивные системы не шумят.

Полученные результаты являются следствием флуктуационно-диссипационной теоремы. В частности она утверждает, что если есть диссипация энергии, то существует и флуктуации энергии.

6. Среднее значение потенциальной энергии при температуре Т.

Потенциальная энергия частицы описывается слагаемым гамильтониана

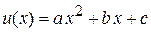, (П.4.11)

где 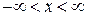; 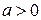. Найти среднее значение потенциальной энергии частицы при температуре T.

Вычисляем потенциальную составляющую статистического интеграла (2.105)

,

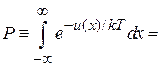
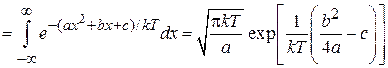где использовано

.

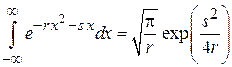Получаем

.

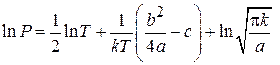Из (2.106)

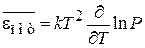
находим

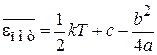. (П.4.12)

При 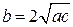потенциальная энергия получает сдвиг аргумента

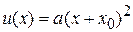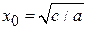, . (П.4.13)

Из (П.4.12) находим

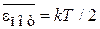. (П.4.14)

В результате сдвиг аргумента потенциальной энергии частицы 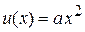не изменяет ее среднего значения при температуре T.

7. Неустранимая погрешность пружинных весов.

Требуется найти гравитационную массу тела m и неустранимую погрешность измерения массы при помощи весов, работающих на основе упругой силы с коэффициентом жесткости κ при температуре Т.

Тело подвешивается на пружину в однородном поле тяжести с ускорением свободного падения g, как показано на рис. 2.15. Пружина растягивается на величину 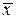. Если тело неподвижно, то проекции силы тяжести 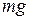и упругой силы 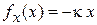, уравновешены

.

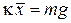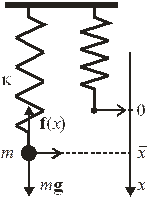
Рис.2.15. Весы на основе упругой силы

Измеряя растяжение пружины 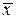, получаем гравитационную массу тела

,

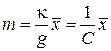где чувствительность весов

.

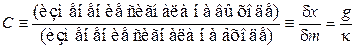Чем меньше коэффициент жесткости, тем выше чувствительность весов и тем сильнее реагирует система на возмущение.

Хаотические тепловые движения молекул пружины, тела и окружающего воздуха приводят к микроколебаниям указателя весов около среднего значения 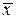. Невозможно снять показания прибора с точностью, меньшей средней амплитуды хаотических колебаний указателя, равной флуктуации

,

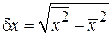где .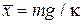

Найдем 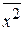, используя теорему о распределении энергии по степеням свободы. Система одномерная, на тело действует результирующая сила с проекцией

,

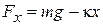тогда потенциальная энергия

, .

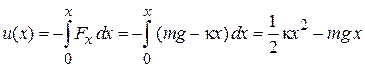Сравнение с (П.4.11)

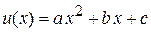
дает

, , .

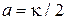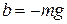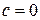Из (П.4.12)

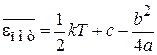
получаем

.

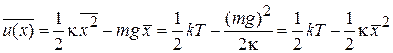В последнем равенстве использовано 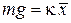. Сравнивая второе и последнее выражения после умножения на 2

.

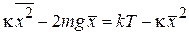С учетом 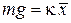находим

, .

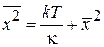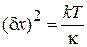В результате минимальная абсолютная погрешность измерения массы

.

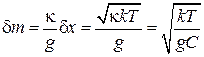Погрешность измерения уменьшается при понижении температуры и увеличении чувствительности весов. Используя частоту свободных колебаний системы 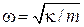, находим относительную погрешность измерения

.

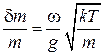При 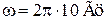, , 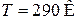, 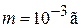получаем .

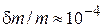8. Неустранимая погрешность пружинных весов (упрощенное описание).

Макрохарактеристика равновесной системы постоянна только в среднем. Ее флуктуация вызвана хаотическими тепловыми движениями микрочастиц.

Измерительное устройство является системой, характеристики которой испытывают тепловые колебания. Невозможно измерить физическую величину с точностью, меньшей средней амплитуды хаотических колебаний указателя прибора. Оценим неустранимую погрешность весов, работающих на основе упругой силы, используя теорему о распределении энергии по степеням свободы.

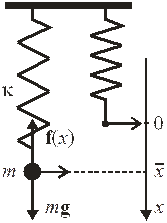
Тело искомой массы подвешено на пружине с коэффициентом жесткости κ в однородном поле тяжести с ускорением свободного падения g. Если тело неподвижно и не ускоряется, то упругая сила

,

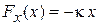вызванная растяжением пружины на расстояние x, и сила тяжести 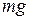уравновешены

.

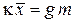Измеряя среднее растяжение пружины 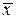, получаем гравитационную массу тела m.

Хаотические тепловые движения молекул пружины и окружающего воздуха приводят к микроколебаниям указателя весов с амплитудой 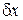и создают погрешность измерения массы 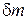. Берем дифференциал условия равновесия сил

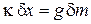
и выражаем через 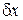абсолютную погрешность измерения массы

,

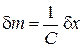где чувствительность весов

.

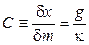Шарик на пружине является одномерным гармоническим осциллятором. Флуктуация относительно среднего положения 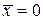равна

,

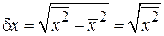где 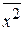найдем из теоремы о распределении тепловой энергии. Потенциальную энергию упругой силы

,

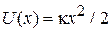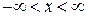
сравниваем с (2.103)

,

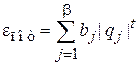находим

, .

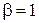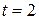Из (2.107)

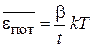
получаем среднюю потенциальную энергию, связанную с одномерным тепловым хаотическим движением весов:

.

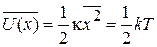Находим

,

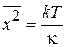получаем флуктуацию указателя весов

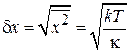
и неустранимую погрешностью измерения массы

.

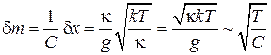Для уменьшения погрешности необходимо уменьшать температуру и увеличивать чувствительность весов. Это требует уменьшениякоэффициента жесткости, который определяет частоту колебаний системы:

.

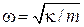Используя 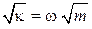, находим относительную погрешность измерения

.

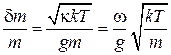Полученный результат применим для любых аналоговых измерительных устройств, использующих упругую силу – вольтметров, амперметров, гальванометров и других устройств.

9. Средняя потенциальная энергия частицыf-мерного газа в поле с радиальной зависимостью потенциальной энергии 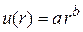, где ; .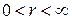

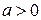Газ при температуре T находится в пространстве с числом степеней свободы 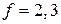. Потенциальная составляющая статистического интеграла (2.105)

,

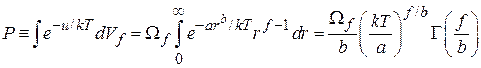где

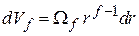– элемент объема f-мерного пространства;

; – элемент телесного угла,

использован интеграл

.

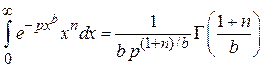Из (2.106)

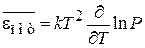
получаем

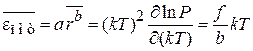. (П.4.15)

10. Центрифуга.

В центрифуге радиусом R, показанной на рисунке, вращающийся с частотой ω газ находится в поле центробежной силы инерции. Потенциальная энергия частицы массой m в полярных координатах на расстоянии r от оси вращения

, .

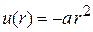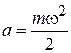Найдем среднюю потенциальную энергию частицы при температуре T и среднее расстояние частицы от оси вращения.

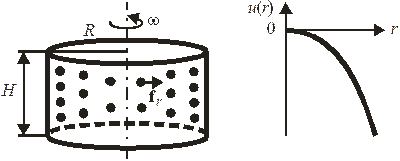
Газ в центрифуге

Потенциальная составляющая статистического интеграла (2.105) в полярных координатах

,

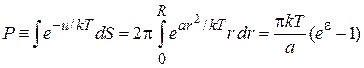где использовано:

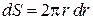– элемент площади;

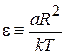– относительная энергия частицы у края центрифуги;

.

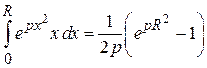Из (2.106)

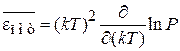
получаем

.

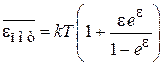В рамках классической статистической физики температура достаточно высока, тогда 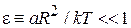. Разлагаем в степенной ряд и удерживаем первые 4 слагаемые

.

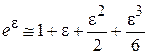Находим

,

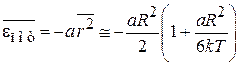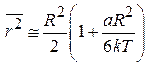. (П.4.16)

Центробежная сила инерции стремится переместить частицы к краю центрифуги. Этому противостоит тепловое движение, разбрасывающее частицы равномерно по всему объему. С увеличением температуры часть частиц оказывается ближе к оси вращения, поэтому с увеличением температуры 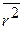уменьшается.

Вопросы коллоквиума

1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.

2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.

3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.

4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц газа при температуре Т. Наиболее вероятные и средние значения.

5. Распределение Больцмана по координате для числа частиц газа при температуре Т во внешнем поле с потенциальной энергией 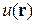. Формула Больцмана для концентрации частиц в однородном поле тяжести.

6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциалы. Условия равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.