Пункт 5. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли

Дифференциальное уравнение вида

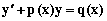. (12)

где 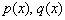– заданные непрерывные функции от x или постоянные, называется линейным дифференциальным уравнением первого порядка.

Его характерным признаком является наличие лишь первых степеней функции 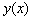и ее производной 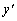. Если 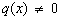, то линейное уравнение называется неоднородным. Если 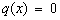, то уравнение

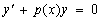. (13)

называется линейным однородным.

Для решения неоднородных линейных уравнений можно использовать: 1) метод Бернулли, или метод подстановки (аналогично тому, как это делалось для однородного относительно переменных x и y уравнения первого порядка); 2) метод вариации произвольных постоянных, или метод Лагранжа, который может быть также использован и для интегрирования линейных дифференциальных уравнений более высоких порядков.

Рассмотрим первый метод подстановки.

Будем искать решение неоднородного линейного уравнения в виде

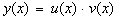. (14)

Для удобства аргумент x в дальнейшем будем опускать. Тогда 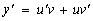. Подставляя (14) в уравнение (12), получим

;

.

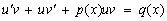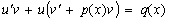Если функцию 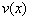выбрать как некоторое решение уравнения с разделяющимися переменными 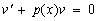(или однородного линейного уравнения), то исходное уравнение примет вид .

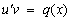Подставляя найденное решение 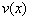в данное уравнение, получим уравнение с разделяющимися переменными относительно переменной x и функции u(x). Если 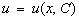– общее решение полученного уравнения, то общее решение исходного линейного уравнения (12) примет вид: 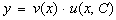, или окончательная формула для определения 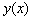имеет вид:

.

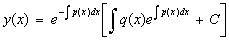Таким образом, интегрирование линейного уравнения (12) сводится к решению двух уравнений с разделяющимися переменными, одно из которых является однородным.

Замечание. Если вместо 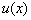и 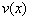подставить полученное после интегрирования значение, то получим, что общее решение линейного, уравнения (12), равное сумме общего решения соответствующего однородного линейного уравнения (13) и частного решения неоднородного линейного уравнения (12).

Примеры:

8. .

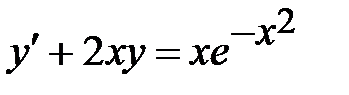Решение:

Будем искать решение уравнения в виде произведения двух функций: 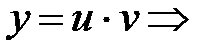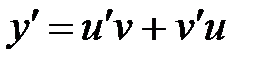. После этой подстановки данное уравнение примет вид: .

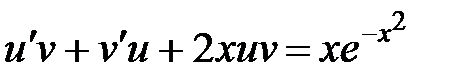Вынесем за скобки u: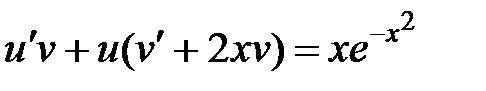

Найдем одну из функций v, такую, чтобы выражение в скобках обратилось в нуль: 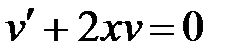. Это уравнение будет с разделяющимися переменными. Решим его.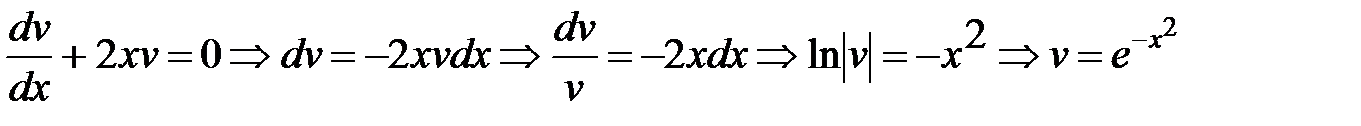

Подставим найденную функцию в уравнение , найденное раньше.

.

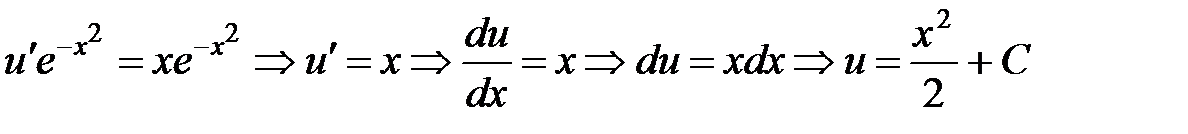Т.к. y = uv, то 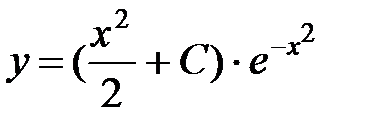- общее решение данного уравнения.

9. .

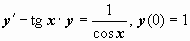Решение:

.

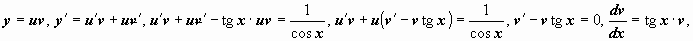
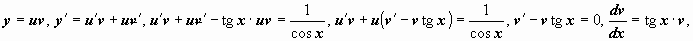
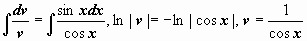Теперь для u(x) получим: 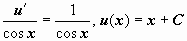, и общее решение уравнения .

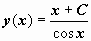Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение .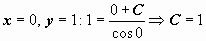

Откуда получаем частное решение: .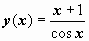

Рассмотрим второй метод Лагранжа.

Метод вариации произвольных постоянных (метод Лагранжа) состоит в следующем.

1) Составляется однородное линейное уравнение (13) соответствующее неоднородному линейному уравнению (12) за счет замены правой части 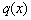на ноль. Это уравнение легко проинтегрировать как уравнение с разделяющимися переменными. Его решением является функция

,

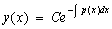где C – произвольная постоянная.

2) Общее решение неоднородного линейного уравнения можно найти исходя из общего решения соответствующего однородного уравнения, варьируя произвольную постоянную, т.е. полагая, что

,

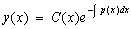где 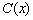– некоторая, подлежащая определению, дифференцируемая функция от x.

Для нахождения 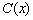нужно подставить 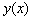в исходное уравнение, что приводит к уравнению с разделяющимися переменными

,

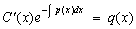которое имеет следующее решение:

,

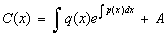где A – произвольная постоянная. Тогда искомое общее решение линейного неоднородного уравнения примет вид

.

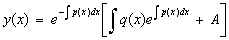Как несложно заметить, полученное решение совпадает с решением, найденным методом Бернулли.

Пример:

10.Решить уравнение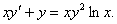

Решение:

Разделим уравнение на xy²: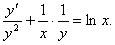

Полагаем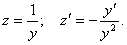

.

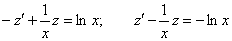Полагаем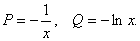

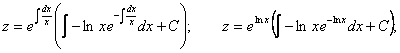
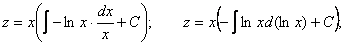
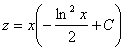
Произведя обратную подстановку, получаем:

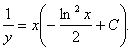
11.Решить уравнение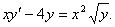

Решение:

Разделим обе части уравнения на :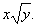

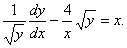
Полагаем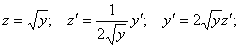

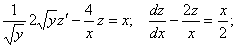
Рассмотрим соответствующее ему линейное однородное уравнение:

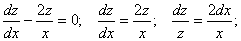
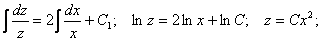
Полагаем C = C(x) и подставляем полученный результат в уравнение, с учетом того, что:

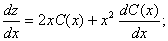
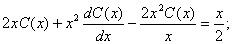
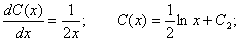
Получаем: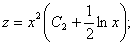

Применяя обратную подстановку, получаем окончательный ответ: 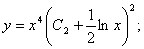.