I. Обращение верхней треугольной матрицы
Практическое занятие 3. Операции с треугольными матрицами
Сведения из теории. Сущность метода обращения верхней треугольной матрицы разберем на матрицах четвертого порядка, а формулы для обращения верхней треугольной матрицы любого порядка приведем без вывода
Пусть А – верхняя треугольная матрица четвертого порядка
А = 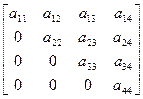 .
.
а искомая обратная ей матрица, элементы которой 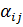 подлежат определению, запишется в виде
подлежат определению, запишется в виде
 =
= 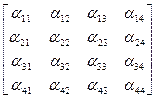 .
.
По определению обратной матрицы должно выполняться равенство
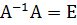
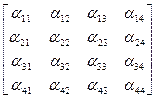 ·
· 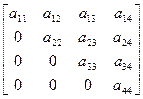 =
= 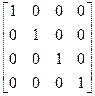 .
.
Используя правило умножения матриц, перемножим матрицы в левой части равенства
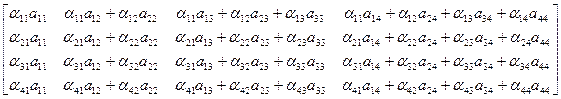 =
=
= 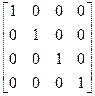 .
.
Исходя из определения равенства двух матриц, для отыскивания неизвестных величин получаем уравнения, сравнив соответствующие элементы первых строк.
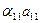 = 1; = 1; | (1) |
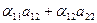 = 0; = 0; | (2) |
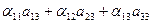 = 0; = 0; | (3) |
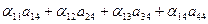 = 0. = 0. | (4) |
Из этих уравнений следует:
из (1) 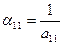 ; ; | (5) |
из (2) 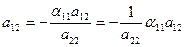 ; ; | (6) |
из (3) 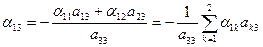 | (7) |
из (4) 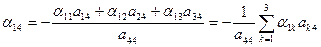 | (8) |
Проделав аналогичную работу для второй, третьей и четвертой строк, получим для второй строки
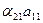 = 0; = 0; | (9) |
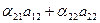 = 1; = 1; | (10) |
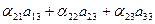 = 0; = 0; | (11) |
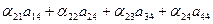 = 0 = 0 | (12) |
из (9) 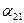 = 0. = 0. | (13) |
С учетом, что 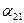 = 0, получаем:
= 0, получаем:
из (10) 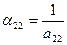 ; ; | (14) |
из (11) 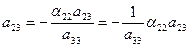 ; ; | (15) |
из (12) 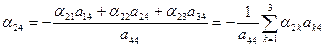 | (16) |
Для третьей строки
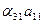 = 0; = 0; | (17) |
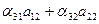 = 0; = 0; | (18) |
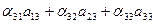 = 1; = 1; | (19) |
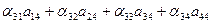 = 0. = 0. | (20) |
Из этих уравнений следует:
из (17) 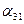 = 0. = 0. | (21) |
Учитывая, что 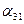 = 0, из (18) получаем
= 0, из (18) получаем
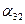 = 0, = 0, | (22) |
а учитывая, что и 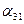 = 0, и
= 0, и 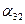 = 0, находим:
= 0, находим:
из (19) 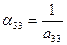 ; ; | (23) |
из (20) 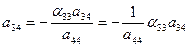 ; ; | (24) |
И наконец, для четвертой строки ищем
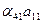 = 0; = 0; | (25) |
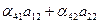 = 0; = 0; | (26) |
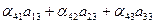 = 0; = 0; | (27) |
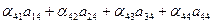 = 1. = 1. | (28) |
Из (25), (26) и (27) следует, что
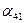 = 0; = 0; | (29) |
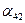 = 0; = 0; | (30) |
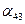 = 0, = 0, | (31) |
| а с учетом этого и (28) получаем | |
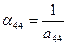 . . | (32) |
Равенства (9), (21), (22), (29), (30) и (31) показывают, что равны нулю те элементы обратной матрицы 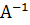 , у которых первый индекс i больше второго индекса j, т.е. если i > j, то
, у которых первый индекс i больше второго индекса j, т.е. если i > j, то
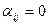 . . | (3.1) |
Из равенства (5), (14), (23), (32) диагональные элементы обратной матрицы 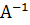 , у которой первый и второй индексы равны (i=j), определяются так:
, у которой первый и второй индексы равны (i=j), определяются так:
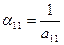 ;
; 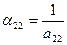 ;
; 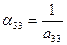 ;
; 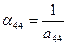 ,
,
что можно объединить одной записью: если i = j, то
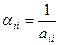 . . | (3.2) |
По формулам (6), (7), (8), (15), (16), (24) и (32) определяются те элементы обратной матрицы для верхней треугольной, у которых первый индекс i меньше второго индекса j (i<j), т.е. элементы, стоящие над главной диагональю. Полученная по этим формулам обратная матрица будет также верхней треугольной.
Когда верхняя треугольная матрица имеет порядок n, элементы обратной ей матрицы находятся по аналогичным формулам, которые имеют следующий вид:
если i = j, то 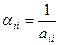 ; ; | (3.3) |
если i > j, то 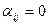 ; ; | (3.4) |
если i < j, то 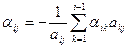 ; ; | (3.5) |
Например, по формуле (3.5) элемент обратной матрицы пятого порядка
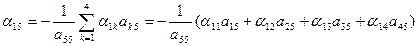 . . | (3.6) |
Замечания. Применяя формулу (3.5), надо иметь в виду, что будут равны нулю те произведения, в которых первый индекс элемента α больше второго индекса. Можно указать простое правило для определения элементов обращенной верхней треугольной матрицы.
1. Определить диагональные элементы обращенной матрицы по формуле (3.3)
2. После этого подписать матрицы одну под другой.
3. На места элементов, стоящих ниже главной, вписать нули.
4. Чтобы определить элемент, стоящий над главной диагональю обратной матрицы, надо составить алгебраическую сумму произведений элементов, стоящих в обратной матрице 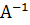 , левее определяемого, на соответствующие элементы того столбца матрицы А (т.е. той матрицы, для которой ищется обратная), в котором стоит определяемый элемент. Эту алгебраическую сумму надо разделить на диагональный элемент матрицы А, стоящий в том же столбце, что и определяемый элемент. Определяемый элемент равен этому частному, взятому с обратным знаком.
, левее определяемого, на соответствующие элементы того столбца матрицы А (т.е. той матрицы, для которой ищется обратная), в котором стоит определяемый элемент. Эту алгебраическую сумму надо разделить на диагональный элемент матрицы А, стоящий в том же столбце, что и определяемый элемент. Определяемый элемент равен этому частному, взятому с обратным знаком.
По этому правилу выражение в скобках в (3.6) получается так: искомый элемент 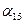 матрицы
матрицы 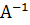 находится в первой строке и пятом столбце. Перед ним в первой строке обратной матрицы
находится в первой строке и пятом столбце. Перед ним в первой строке обратной матрицы 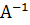 стоят элементы
стоят элементы 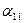 ,
, 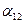 ,
, 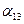 и
и 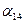 , а в пятом столбце матрицы А – элементы
, а в пятом столбце матрицы А – элементы 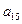 ,
, 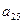 ,
, 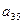 и
и 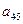 . Составляется алгебраическая сумма произведений первого элемента в первой строке матрицы
. Составляется алгебраическая сумма произведений первого элемента в первой строке матрицы 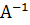 на второй элемент в пятом столбце матрицы А и т.д. Для уяснения этого правила решим несколько задач.
на второй элемент в пятом столбце матрицы А и т.д. Для уяснения этого правила решим несколько задач.
Задача 3.1 Найти обратную матрицу для матрицы
А =  .
.
Решение.п. 1.Находим диагональные элементы 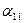 ,
, 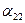 ,
, 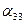 и
и 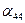 обращенной матрицы по формуле (3.3)
обращенной матрицы по формуле (3.3)
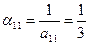 ;
; 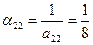 ;
; 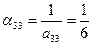 ;
; 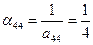 .
.
пп. 2 и 3. Подписываем матрицы одну под другой и вписываем нули на места элементов, стоящих под главной диагональю
А = 
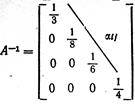
п. 4. Определяем элементы 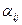 , стоящие над главной диагональю (i < j), по формуле (3.5), пользуясь указанным в п.4 правилом.
, стоящие над главной диагональю (i < j), по формуле (3.5), пользуясь указанным в п.4 правилом.
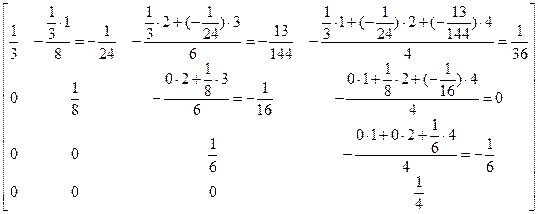 ;
;
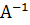 =
= 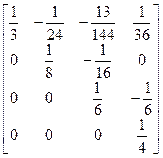
Для проверки надо перемножить матрицы А и 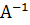 и убедится, что получится единичная матрица
и убедится, что получится единичная матрица
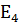 =
= 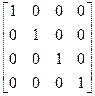 .
.
При решении этой задачи все элементы обратной матрицы были представлены в виде простых дробей для облегчения контроля. На практике же все вычисления ведутся в десятичных дробях.
