Обернена матриця
Означення.Матриця А–1 називається оберненою матрицею до квадратної невиродженої матриці А, якщо виконується співвідношення: 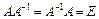 .
.
Нехай дано квадратну матрицю А. Доведемо, що коли 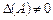 , існує обернена матриця А–1. Розглянемо матрицю:
, існує обернена матриця А–1. Розглянемо матрицю:
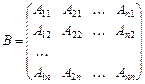 . Утворимо добутки
. Утворимо добутки 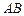 і
і  .
.
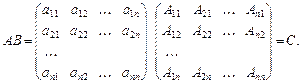
За правилом множення матриць елементи матриці С знаходимо за формулою:
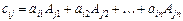 . (1.6)
. (1.6)
Якщо i = j, то згідно з формулою (1.3) маємо: 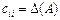 , тобто знаходимо значення визначника матриці А; якщо
, тобто знаходимо значення визначника матриці А; якщо 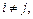 то вираз (1.6) є сумою добутків елементів i-го рядка визначника на алгебраїчні доповнення, що відповідають j-му рядку цього самого визначника. За властивістю 9 визначників така алгебраїчна сума дорівнює нулю. Отже,
то вираз (1.6) є сумою добутків елементів i-го рядка визначника на алгебраїчні доповнення, що відповідають j-му рядку цього самого визначника. За властивістю 9 визначників така алгебраїчна сума дорівнює нулю. Отже, 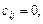 якщо i ¹ j. Матриця С набирає вигляду:
якщо i ¹ j. Матриця С набирає вигляду: 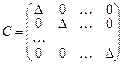 . Щоб ця матриця стала одиничною, треба помножити її на
. Щоб ця матриця стала одиничною, треба помножити її на 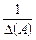 .
.
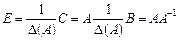 .
.
Отже, обернена матриця має вигляд:
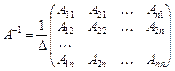 .
.
Доведемо, що для матриці А матриця А–1 єдина. Для цього припустимо протилежне. Нехай існує одна матриця С, така що АС = СА = Е. Тоді
САА–1 = С(АА–1) = СЕ = С,
а водночас
САА–1 = (СА)А–1 = ЕА–1 = А–1, звідси С = А–1.
Доходимо висновку, що початкове припущення неправильне, тобто обернена матриця єдина.
Повернемось тепер до виразу (1.5) — запису системи рівнянь у матричному вигляді АХ = В. Припустимо, що система складається з n лінійних рівнянь з n невідомими, матриця А — квадратна і 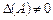 — матриця невироджена. Тоді для матриці А побудуємо обернену А–1 — вона за тих припущень, які щойно зроблено, існує. Помноживши тепер матричну рівність АХ = В зліва на матрицю А–1, дістанемо:
— матриця невироджена. Тоді для матриці А побудуємо обернену А–1 — вона за тих припущень, які щойно зроблено, існує. Помноживши тепер матричну рівність АХ = В зліва на матрицю А–1, дістанемо:
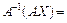
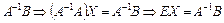 ,
,
або остаточно 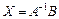 .
.
Останній вираз — це розв’язок системи лінійних рівнянь. Зауважимо, що в такому вигляді можна записати розв’язок будь-якого матричного рівняння, якщо матриця А задовольняє умови існування А–1.
8. Ранг матриці
Розглянемо матрицю А розміром 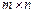
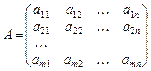
і введемо ще одне важливе поняття.
Означення. Рангом матриці А розміром 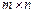 називається найвищий порядок відмінного від нуля мінора, утвореного з елементів цієї матриці. Зрозуміло, що
називається найвищий порядок відмінного від нуля мінора, утвореного з елементів цієї матриці. Зрозуміло, що 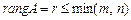 , а найбільший можливий ранг матриці може дорівнювати меншому з чисел m і n.
, а найбільший можливий ранг матриці може дорівнювати меншому з чисел m і n.
Обчислюючи ранг матриці, потрібно переходити від мінорів менших порядків, відмінних від нуля, до мінорів більших порядків. Якщо вже знайдено відмінний від нуля мінор М k-го порядку, то достатньо обчислити лише мінори 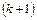 -го порядку, що обводять мінор М. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює k. Якщо серед них знайдеться такий, що відмінний від нуля, то далі для нього будуються обвідні мінори
-го порядку, що обводять мінор М. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює k. Якщо серед них знайдеться такий, що відмінний від нуля, то далі для нього будуються обвідні мінори 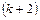 -го порядку і т. д.
-го порядку і т. д.
Означення. Елементарними перетвореннями матриці А називаються такі її перетворення:
1) заміна місцями двох рядків або двох стовпців матриці;
2) множення рядка або стовпця матриці на довільне відмінне від нуля число;
3) додавання елементів одного рядка або стовпця до відповідних елементів іншого рядка або стовпця, попередньо помноженого на деяке число.
Теорема. Елементарні перетворення не змінюють рангу матриці.
Далі матриці, які мають рівні ранги, називатимемо еквівалентними матрицями. Еквівалентні матриці об’єднуватимемо знаком «~» («тильда»).
