Аксиоматическое построение системы натуральных чисел
ОЗО МАТЕМАТИКА 1 курс 2 семестр
Пример 1: Обоснуем выбор действия при решении задачи: «Купили 4 пачки цветной бумаги, а белой на 3 пачки больше. Сколько пачек белой бумаги купили?»
Решение. В задаче речь идет о двух множествах. Пусть А - множество пачек цветной бумаги, В - множество пачек белой бумаги. По условию известно число пачек цветной бумаги, т.е. n(A)=4, а численность множества В требуется найти. Кроме того, согласно условию задачи в множестве В можно выделить подмножество С, численность которого равна 3, т.е. n(C)=3. Сделаем это, например, так, как показано на рис. 1.










 А: В:
А: В:
В1 С
Рисунок 1
Тогда разность В \ С = В1 будет равномощна множеству А, т.е. n(B1) = n(A).
Таким образом, множество В является объединением множеств В1 и С, где В1 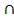 С=Æ.
С=Æ.
Задача сводится к определению численности объединения двух непересекающихся множеств и решается действием сложения: n(B) = n(B1 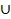 С) = n(B1) + n(C); n(B) = 4+3 = 7.
С) = n(B1) + n(C); n(B) = 4+3 = 7.
Пример 2: Используя понятие числа как меры величины, обоснуем выбор действия при решении задачи: «На юбку израсходовали 3м ткани, а на блузку 2м. Сколько метров ткани пошло на весь костюм?»
Решение: В задаче речь идет о величине – длина, которая измеряется при помощи единицы величины 1метр, т.к. величина длина непрерывная, то объяснить выбор действия при решении задачи будем при помощи отрезков (рис.2).
Пусть е=1м, отрезок а показывает длину ткани, израсходованной на юбку, а=3е. Отрезок в показывает длину ткани, израсходованной на блузку, в=2е. Т.к. в задаче требуется узнать количество всей израсходованной ткани, то отрезок с будет обозначать количество всей израсходованной ткани: с = а + в.
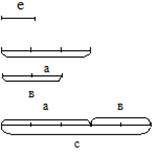 Рисунок 2 Рисунок 2 | а=3е в=2е mе(с)= me(a)+mе(в) mе(с) = 2+3 m е(с) = 5 Ответ: 5 м. |
Пример 3: Используя понятие числа как меры величины, обоснуем выбор действия при решении задачи: «В первом ящике было 12кг печенья, а во втором на 3кг меньше. Сколько килограммов печенья было во втором ящике?»
Решение: В задаче речь идет о величине масса, единица измерения которой 1килограмм, е = 1 кг, т.к. величина, масса непрерывная, то объяснять выбор действия при решении задачи будем при помощи отрезков (рис.3).
Пусть е=1кг, отрезок а показывает сколько килограммов печенья было в первом ящике, а = 12е.
Отрезок b показывает на сколько килограммов печенья было во втором ящике меньше, чем в первом, в = 3е.
Отрезок с показывает сколько килограммов печенья было во втором ящике, me(с) - ? Известно, что во втором ящике на 3 кг печенья меньше, чем в первом, т.е. столько же, но на 3 меньше.
| Пусть d=a, тогда c = d – b. а = 12е, значит d = 12е. me(c)= me(d)-me(в) me(c)=12-3 me(c)=9 | 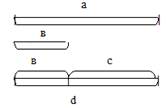 Рисунок 3 Рисунок 3 |
Ответ: 9 килограммов печенья было во втором ящике.
Задачи для самостоятельного решения при подготовке
к зачету (1 курс, 2 семестр)
Аксиоматическое построение системы натуральных чисел
1. Примените законы операций и вычислите результат; каждый случай использования законов объясните:
а) 7091 + (1819 + 509); б) (9073 + 1329) + 2671;
в) 386 + 287 + 213 + 564; г) 3057 + 1561 + 1513 + 829 + 2564;
д) (372 ž 4) ž 5; е) 125 ž 15 ž 6 ž 8;
ж) 20 ž 811 ž 4; з) 350 ž 44ž 20 ž 50.
и) 57 ž 247 + 57 ž 362; к) 37 ž 42 + 37 ž 36 - 78 ž 27;
л) 47 ž 3 + 53 ž 3; м) 5(12+25).
2. Обладает ли операция деления на множестве натуральных чисел свойством коммутативности? Свойством ассоциативности? Ответ обоснуйте.
