Расчет цепи однофазного синусоидального тока символическим методом
Методические указания к расчетно-графической работе № 2
по дисциплине “Электротехника” для студентов
неэлектрических специальностей
Курск 2007
Составители И.С.Некрасов, Е.П. Пахомова
УДК 621.3
Рецензент
Кандидат технических наук, доцент кафедры вычислительной техники
В.И.Иванов
Расчет цепи однофазного синусоидального тока символическим методом: Методические указания к расчетно-графической работе/ Курск. гос. техн. ун-т; Сост. И.С.Некрасов, Е.П.Пахомова. Курск, 2007, 11 с.
Содержатся методические указания по расчету электрических цепей переменного тока символическим методом и задания для выполнения расчетно-графической работы.
Работа предназначена для студентов неэлектрических специальностей.
Табл. 2. Ил. 1. Библиогр.: 4 назв.
Текст печатается в авторской редакции
ЛР №020280 от 09.12.06. ПДЛ № 50-25 от 01.04.07.
Подписано в печать .Формат 60х84 1/16. Печать офсетная.
Усл. печ. л. .Уч.-изд.л. Тираж 150 экз. Заказ .
Курский государственный технический университет.
Издательско-полиграфический центр Курского государственного технического университета. 305040 Курск, ул. 50 лет октября,94.
1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Приступая к выполнению расчетно-графической работы, следует повторить основные положения раздела электротехники “Электрические цепи синусоидального тока”. Работа выполняется с целью приобретения и закрепления навыков расчета цепей переменного тока.
Отчет о выполнении расчетно-графической работы должен содержать:
1) титульный лист;
2) расчетно-пояснительную записку;
3) список используемой литературы.
Пояснительная записка должна включать в себя следующие необходимые разделы.
1. Задание на выполнение расчетов, которое оформляется на втором листе пояснительной записки и содержит электрическую схему к расчету и программу исследования электрической цепи.
2. Расчеты, графики и диаграммы, предусмотренные программой. При выполнении каждого пункта задания необходимо выполнять заново чертеж преобразованной схемы. Все расчеты должны сопровождаться пояснительным текстом. При записи вычислений после числового значения рассчитываемой величины необходимо указывать сокращенное обозначение единиц измерения.
3. Сводная таблица результатов, которая приводится в конце расчетов.
Расчетно-пояснительная записка оформляется на листах формата А4 в соответствии с требованиями ЕСКД.
Все элементы электрической схемы следует изображать в соответствии со стандартными условными графическими обозначениями, используя чертежные инструменты. Около условных графических обозначений необходимо проставлять буквенные обозначения основных параметров (сопротивление — R, емкость — С, индуктивность — L, ЭДС — Е и т.д.). Узлы электрической схемы могут быть обозначены буквами латинского алфавита (a, b, c, d...) либо цифрами (1, 2, 3...). При обозначении токов, сопротивлений и напряжений в различных ветвях схемы необходимо использовать индексы. В качестве нижних индексов могут применяться арабские или римские цифры, строчные буквы русского, латинского и греческого алфавитов, например:
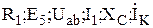и т. д.
В качестве верхних индексов допускаются штрихи и римские цифры, например:
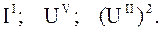
В случае, когда одним обозначением заменяется разность двух величин, первая буква или цифра относится к уменьшаемому, а вторая — к вычитаемому:
.
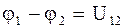Применение индексов с тремя буквами или цифрами не допускается.
2. ЗАДАНИЕ НА ВЫПОЛНЕНИЕ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
1. Найти действующие значения токов во всех ветвях электрической схемы символическим методом.
2. Составить баланс активных и реактивных мощностей.
3. Построить топографическую диаграмму напряжений и лучевую для токов.
Номер варианта состоит из трех цифр. Первая цифра в номере варианта соответствует номеру исходной схемы (рис. 2.1). Вторая цифра в номере варианта соответствует порядковому номеру строки в табл. 2.1, в которой заданы значения реактивных сопротивлений исходной схемы. Третья цифра в номере варианта соответствует порядковому номеру строки в табл. 2.2, содержащей значения активных сопротивлений ветвей исходной схемы и напряжения на входе этой схемы.
Таблица 2.1 Таблица 2.2
| № | X1, Ом | X2, Ом | X3, Ом | X4, Ом | № | U, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | jU, град | |
| -45 | ||||||||||||
| -20 | ||||||||||||
| -30 | ||||||||||||
| -45 | ||||||||||||
| -60 |
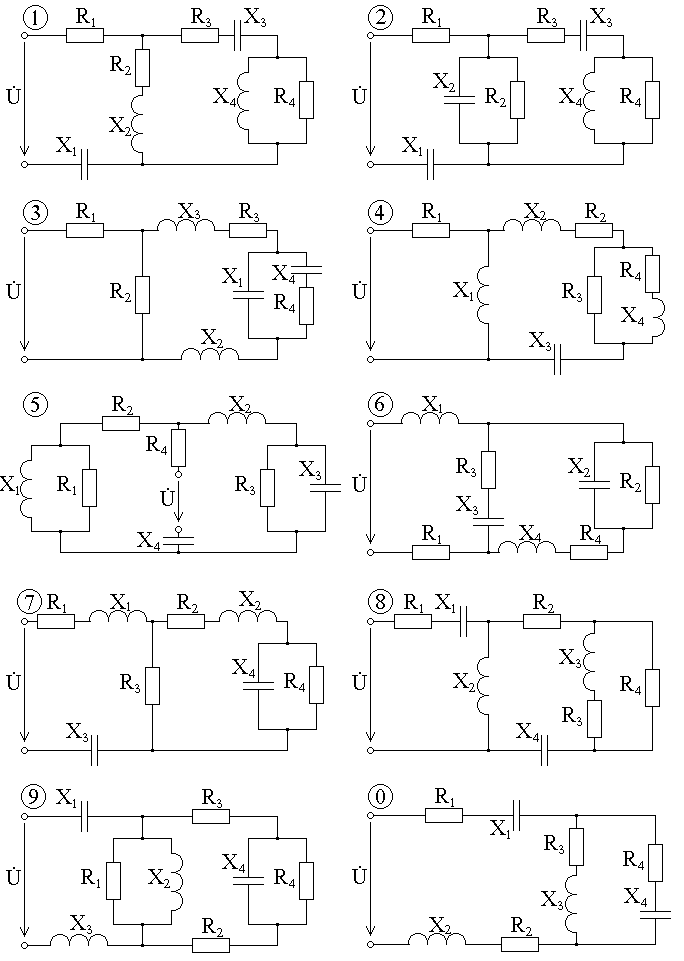
Рис 2.1.
3. ПРИМЕНЕНИЕ СИМВОЛИЧЕСКОГО МЕТОДА ДЛЯ РАСЧЕТА ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
При расчете электрических цепей часто приходится складывать, вычитать или просто качественно сопоставлять величины токов, напряжений, ЭДС, являющихся синусоидальными функциями времени. При этом графические построения или тригонометрические вычисления могут оказаться очень громоздкими. Однако задача может упроститься, если оперировать не с синусоидальными функциями времени, а с векторами, проекции которых на ось координат при их вращении образуют синусоидальные функции. Если зафиксировать положение векторов в определенный момент времени, то можно получить так называемую “векторную диаграмму”.
Векторные диаграммы являются удобным и эффективным средством качественного анализа электрических цепей. В некоторых случаях они могут быть использованы и для расчетов. Однако для этого удобнее пользоваться не геометрическими построениями (правила параллелограмма, треугольника, вычитания векторов), а алгебраическим суммированием их проекций на две взаимно перпендикулярные оси. Так каждый из слагаемых векторов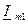 
и 
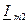на рис. 3.1. может быть представлен в виде двух проекций на оси координат 
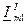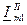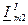и 
, 
и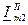 
. Затем можно алгебраически сложить соответствующие проекции, получив проекции результирующего вектора 
.
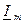Приведенные выше рассуждения положены в основу двух методов анализа цепей синусоидального тока. Первый — метод разложения векторов на составляющие, которые при соответствующем выборе расположения осей называют активными и реактивными.
Второй метод заключается в следующем. Рассмотрим векторную диаграмму на комплексной плоскости (рис. 3.1):
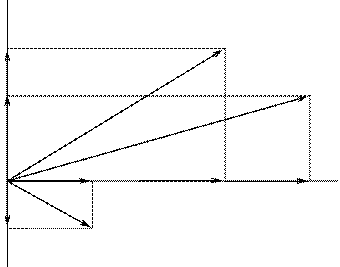(+j)
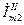
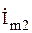
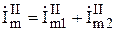
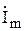
0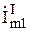 
(+)
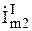
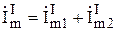
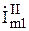
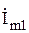
Рис. 3.1.
пусть горизонтальная ось будет осью вещественных величин, а вертикальная — осью мнимых величин (в отличие от математики в электротехнике мнимую единицу обозначают не i, а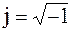 
, чтобы не путать с обозначением тока). Тогда вектор 
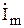(см. рис. 3.1) может быть описан с помощью комплексных выражений одним из следующих способов:
.
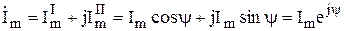Первая форма записи называется алгебраической, вторая — тригонометрической, третья — показательной. В основе взаимного перехода показательной и тригонометрической форм записи лежит формула Эйлера: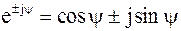 
.
Модуль комплексного числа, в частности тока, вычисляется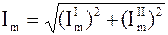 
, а аргумент — 
.
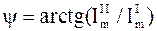Сопряженный комплекс тока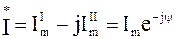 
.
В частном случае, когда поворот вектора осуществляется на угол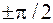 
, из формулы Эйлера следует:
.
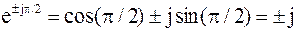Таким образом, умножение комплексного числа на множитель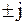 
означает поворот соответствующего вектора на угол .
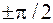Аналогично, с помощью комплексных чисел может быть описан вектор напряжения.
Описание в символической форме сопротивлений цепи переменного тока определяется характером их воздействия на сдвиг фаз между током и напряжением. Умножение вектора тока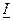 
на активное сопротивление R изменяет только величину вектора, а умножение этого же вектора на индуктивное сопротивление 
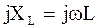не только изменяет длину вектора, но и поворачивает его на 90 
в положительную сторону (против часовой стрелки). Умножение вектора на емкостное сопротивление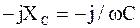 
изменяет длину вектора и поворачивает его на 90 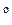в отрицательную сторону.
Если цепь будет содержать как активное R, так и реактивное X сопротивления, то полное сопротивление такой цепи будет комплексной величиной. Полное сопротивление обозначают прописной буквой Z, а модуль полного сопротивления — строчной буквой z:
; 
.
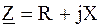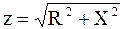Комплексом мощности называется произведение комплекса напряжения на сопряженный комплекс тока:
,
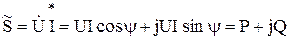где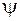 
— угол сдвига фаз между током и напряжением, P — действительная часть комплексной мощности (активная мощность), Q — мнимая часть комплексной мощности (реактивная мощность).
Изображение проводимостей переменного тока в символической форме обосновывается так же, как и изображение сопротивлений: активная проводимость G является действительной величиной, индуктивная — мнимой отрицательной -jBL, а емкостная — положительной jBC.
Полная проводимость есть комплексная величина
.
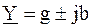На использовании комплексных выражений электрических величин основан символический метод анализа электрических цепей, в котором действия над вещественными функциями времени заменяются более простыми действиями над комплексными числами, благодаря чему становится возможным применение всех методов расчета цепей постоянного тока (законы Кирхгофа, метод контурных токов, метод наложения и т.д.).
Символический метод расчета цепей синусоидального тока является самым распространенным. Он позволяет при выполнении различных действий над электрическими величинами учитывать как абсолютные значения этих величин (модули), так и их фазы (аргументы).
Методику расчета электрических цепей переменного тока с использованием символического метода рассмотрим на примере решения задачи.
1. Определить токи и мощности во всех ветвях электрической цепи (рис. 3.2), если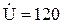 
В; L0=0,01274 Гн; L1=0,02548 Гн; R1=6 Ом; R2=5 Ом; C=636 мкФ; f=50 Гц.
2. Составить баланс активных и реактивных мощностей.
3. Построить топографическую диаграмму для напряжений и лучевую для токов.
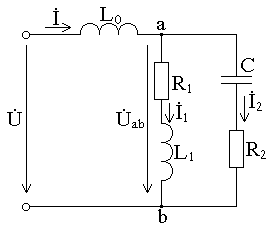
Рис. 3. 2.
Используя метод эквивалентных преобразований исходную схему можно привести к виду рис. 3.3.
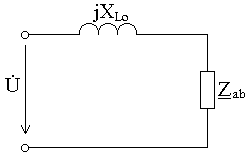
Рис. 3.3.
В этой схеме сопротивление Z ab вычисляется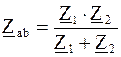 
, где Z1=R1+jXL1; Z2=R2 — jXC.
Входное комплексное сопротивление цепи рис.3.3 можно вычислить следующим образом:
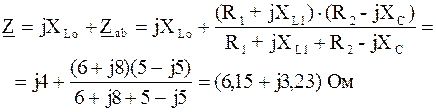
Теперь определяем общий ток цепи
.
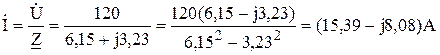Модуль или действующее значение этого тока будет равно
.
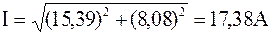Определяем комплексное напряжение на сопротивлении
.
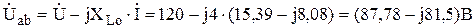Модуль или действующее значение этого напряжения:
.
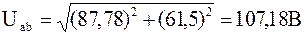Теперь определяем ток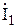и 
и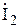 
и их абсолютные значения:
,
,
,
.
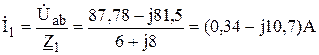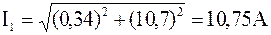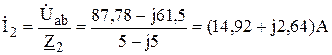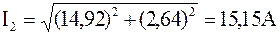Комплексная полная мощность всей цепи
.
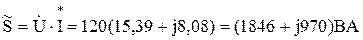Откуда Р=1846 Вт, Q=970 Вар.
Правильность вычислений проверяем составлением баланса мощностей. Для этого подсчитываем активные и реактивные мощности отдельных ветвей цепи.
.
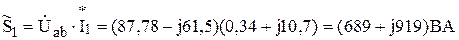Откуда Р1=689 Вт, Q1=919 ВАр.
.
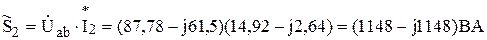Откуда Р2=1148 Вт, Q2=-1148 ВАр.
Активная и реактивная мощности всей цепи соответственно равны
Р1+Р2=689+1148=1837 Вт,
Q1+Q2+Q0= Q1+Q2+XLoI2=919-1148+1206=977 ВАр.
Незначительное расхождение с ранее найденными значениями активной и реактивной мощностей объясняется округлением чисел при вычислении.