Понятие непрерывной функции
Понятие непрерывности функции является одним из основных понятий математического анализа.
Определение 5.1.Функция у = f(x), определённая на интервале 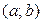 , называется непрерывной в точкех0
, называется непрерывной в точкех0 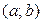 , если
, если 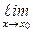 f(x) = f(x0).
f(x) = f(x0).
Пример 5.1.Доказать непрерывность функции f(x) = 2х2 + 2х +1 в точке х0 = 1.
Решение.Находим:
1) 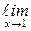 f(x) =
f(x) = 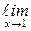 (2х2 + 2х +1) = 2
(2х2 + 2х +1) = 2 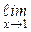 x2 + 2
x2 + 2 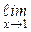 x +
x + 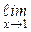 1 = 2 × 1 + 2 × 1 + 1 = 5.
1 = 2 × 1 + 2 × 1 + 1 = 5.
2) f(1) = 2 × 12 + 2 × 1 + 1 = 5.
Так как 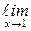 f(x) = f(1), то по определению функция f(x) непрерывна в точке х0 = 1.
f(x) = f(1), то по определению функция f(x) непрерывна в точке х0 = 1.
Определение 5.2.Пусть х0, х0 Î 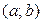 . Разность ∆х = х − х0 называется приращением аргумента в точкех0, а разность ∆у = f(x) − f(x0) = f(x0 + ∆x) − f(x0) – приращением функции в точке х0.
. Разность ∆х = х − х0 называется приращением аргумента в точкех0, а разность ∆у = f(x) − f(x0) = f(x0 + ∆x) − f(x0) – приращением функции в точке х0.
Теорема 5.1.Функция у = f(x) непрерывна в точке х0 Î 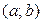 тогда и только тогда, когда
тогда и только тогда, когда 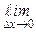 ∆у = 0.
∆у = 0.
Доказательство.1 Пусть функция у = f(x) непрерывна в точке х0 Î 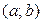 . Это означает, что
. Это означает, что 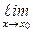 f(x) = f(x0). Положим х = х0 + ∆х. Получим
f(x) = f(x0). Положим х = х0 + ∆х. Получим
 f(x0 + ∆x) = f(x0),
f(x0 + ∆x) = f(x0),
откуда  f(x0 + ∆x) −
f(x0 + ∆x) −  f(x0) = 0,
f(x0) = 0,  ((x0 + ∆x) − f(x0)) = 0,
((x0 + ∆x) − f(x0)) = 0,
т. е. 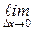 ∆у = 0.
∆у = 0.
2 Пусть теперь  ∆у = 0. Тогда
∆у = 0. Тогда  ((x0 + ∆x) − f(x0)) = 0, откуда
((x0 + ∆x) − f(x0)) = 0, откуда 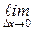 f(x0 + ∆x) −
f(x0 + ∆x) −  f(x0) = 0,
f(x0) = 0,  f(x0 + ∆x) = f(x0). Это означает, что функция у = f(x) непрерывна в точке х0.
f(x0 + ∆x) = f(x0). Это означает, что функция у = f(x) непрерывна в точке х0.
Теорема 5.2.Если функции f(x) и φ(х) непрерывны в точке х0, то непрерывны в этой точке их сумма f(x) + φ(x), разность f(x) − φ(x), произведение f(x) × φ(x), а также частное f(x)/φ(x) при условии, что φ(х0) ≠ 0.
Доказательство этой теоремы непосредственно следует из определения непрерывности и свойств пределов функций.
Например, непрерывными являются многие элементарные функции:
1) целая рациональная функция Pn(x) = 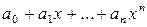 непрерывна при всех х Î R;
непрерывна при всех х Î R;
2) дробно-рациональная функция R(x) =  непрерывна при всех х, для которых знаменатель не обращается в нуль;
непрерывна при всех х, для которых знаменатель не обращается в нуль;
3) тригонометрические функции у = sinx, y = cosx, y = tgx, y = ctgx непрерывны во всех точках области определения.
Теорема 5.3. Пусть функция z = φ(x) непрерывна в точке х0, а функция у = f(z) непрерывна в точке z0 = φ(x0). Тогда сложная функция у = f(φ(x)) непрерывна в точке х0.
Эта теорема позволяет сделать вывод о непрерывности функций, которые являются композициями непрерывных функций.
Пример 5.2.Доказать, что функция у = sinx2 непрерывна в точке х0 = 0.
Решение.Функция z = x2 непрерывна в точке х0 = 0 как целая рациональная функция. Функция у = sinz непрерывна в точке z0 = x02 = 0, то по теореме 5.3 сложная функция у = sinz = sinx2 непрерывна в точке х0 = 0.
Определение 5.3.Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала. Если функция определена при х =  и при этом
и при этом 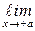 f(x) = f(
f(x) = f(  ), то говорят, что f(x) в точке
), то говорят, что f(x) в точке  непрерывна справа.Аналогично, если
непрерывна справа.Аналогично, если  f(x) = f(
f(x) = f(  ), то говорят, что f(x) в точке
), то говорят, что f(x) в точке  непрерывна слева.Функция называется непрерывной на
непрерывна слева.Функция называется непрерывной на  ,если она непрерывна в каждой его точке (в точке
,если она непрерывна в каждой его точке (в точке  – непрерывна справа, в точке
– непрерывна справа, в точке  – непрерывна слева).
– непрерывна слева).
Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.
Теорема 5.4. (первая теорема Больцано-Коши).
Пусть функция f(x) непрерывна на [ 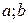 ] и на концах отрезка имеет значения разных знаков. Тогда существует точка
] и на концах отрезка имеет значения разных знаков. Тогда существует точка  Î [
Î [ 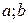 ], в которой f(
], в которой f(  ) = 0.
) = 0.
Теорема 5.5.(вторая теорема Больцано-Коши).
Пусть функция f(x) непрерывна на [  ], причём f(
], причём f(  ) = A, f(
) = A, f(  ) = B. Пусть С – любое число, заключённое между А и В. Тогда на отрезке [
) = B. Пусть С – любое число, заключённое между А и В. Тогда на отрезке [  ] найдётся точка
] найдётся точка  такая, что f(
такая, что f(  ) = C.
) = C.
Теорема 5.6. (первая теорема Вейерштрасса).
Если функция f(x) определена и непрерывна на [  ], то она ограничена на этом отрезке.
], то она ограничена на этом отрезке.
Теорема 5.7.(вторая теорема Вейерштрасса).
Если функция f(x) непрерывна на [  ], то она достигает на этом отрезке своего наименьшего значения и своего наибольшего значения, т. е. существуют такие точки х1, х2 Î [
], то она достигает на этом отрезке своего наименьшего значения и своего наибольшего значения, т. е. существуют такие точки х1, х2 Î [  ], что для всех х Î [
], что для всех х Î [  ] f(x1) £ f(x) £ f(x2).
] f(x1) £ f(x) £ f(x2).
