Метод эйлера решения задачи коши

Рассмотрим дифференциальное уравнение

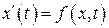. (8.1)

Предположим, что функция 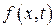дифференцируема в некоторой окрестности точки 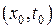. Задача Коши для дифференциального уравнения (8.1) формулируется следующим образом: найти решение 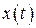уравнения (8.1), удовлетворяющее условию .

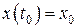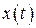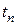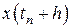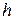Предположим, что известно решение в точке и требуется найти , где – шаг интегрирования. Согласно формуле Ньютона – Лейбница, очевидным является следующее равенство

.

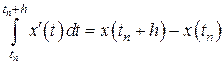Запишем его следующим образом

.

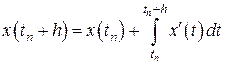Учитывая уравнение (8.1), последнее равенство можно записать в виде

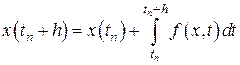. (8.2)

Интеграл в правой части выражения (8.2) приближенно можно вычислить, используя формулу прямоугольников:

.

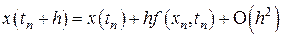Здесь 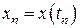. Отбрасывая члены порядка 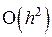и полагая 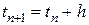, , 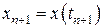получаем известную формулу Эйлера

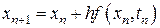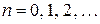, . (8.3)

Аналогичный результат можно получить и другим способом. Для этого разложим функцию 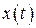в ряд Тэйлора в окрестности точки 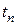, в результате получим

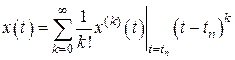(8.4)

или

.

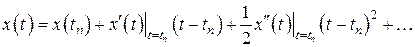В последнем выражении ограничимся двумя первыми слагаемыми в правой части. В результате получаем

, .

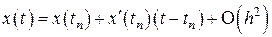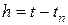Полагаем, что решение 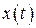в точке 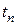известно. Тогда решение в точке 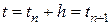можно найти, используя последнюю формулу и учитывая, что :

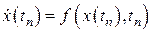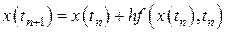(8. )

или

, .

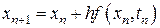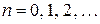Начинать вычислительный процесс необходимо с точки, определяющей начальные условия, то есть .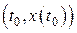

Вычислительный процесс, построенный по формуле (8.3), имеет локальную погрешность, пропорциональную 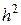. Это означает, что на каждом шаге интегрирования имеет место погрешность порядка 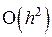. Соответственно, при увеличении времени интегрирования общая погрешность решения дифференциального уравнения возрастает.

Повысить точность получаемых результатов можно, если учитывать большее количество членов разложения функции 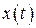в ряд Тэйлора. Однако, для этого необходимо последовательно дифференцировать правую часть дифференциального уравнения (8.1).

Рассмотрим это на конкретном примере.

Учтем первые четыре члена в ряде Тэйлора, в результате получим

.

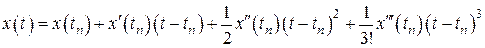Как и ранее, полагаем, что решение в точке 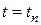найдено. Выбирая достаточно малый шаг 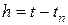, находим решение в следующей точке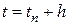

.

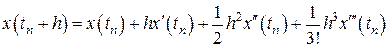Для реализации этой формулы необходимо знать производные искомого решения 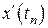, , 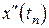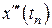. Первая производная 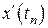может быть найдена из дифференциального уравнения (8.1). Это есть его правая часть, 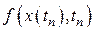. Вторую и третью производные решения – 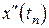, 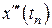– можно найти, дифференцируя правую часть уравнения (8.1), рассматривая ее, как сложную функцию. Соответственно имеем

,

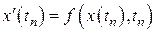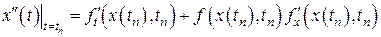, (8.5)

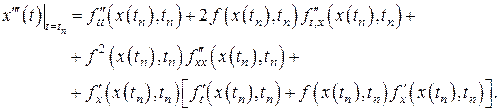
Как видим, такой путь повышения локальной точности решения дифференциального уравнения (2.1) является трудоемким.

Точность вычислений можно повысить при заданном шаге интегрирования 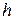и другими способами. В формуле (8.2) интеграл вычисляется по формуле прямоугольников. Вычислим этот интеграл, используя формулу трапеций. В результате будем иметь

.

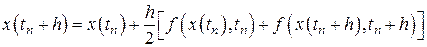По формуле Тэйлора, справедливо равенство

.

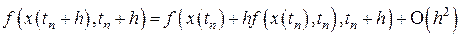Отбрасывая в последнем выражении члены порядка 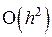, и полагая

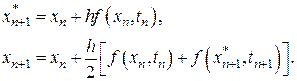(8.6)

Здесь .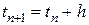

Погрешность, которая обеспечивается этими формулами, имеет порядок 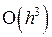. Формулы (8.6) называются формулами Эйлера – Коши.

МЕТОДЫ РУНГЕ – КУТТА

Полагаем, что функция 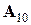имеет непрерывные частные производные до 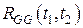-го порядка включительно, тогда решение задачи Коши для уравнения (8.1) будет обладать непрерывными производными до -го порядка включительно. Если значение известно в точке , то справедливо равенство

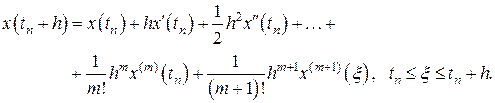(8.7)

Как уже отмечалось, значения входящих в данную формулу производных вычисляются последовательным дифференцированием уравнения (8.1), что является достаточно трудоемким процессом.

Для сокращения вычислительной работы Рунге предложил искать значение 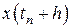в виде

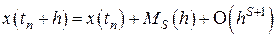, (8.8)

где

,

,

,

…

,

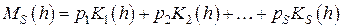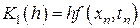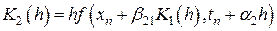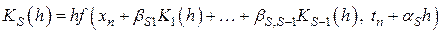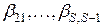; ; – некоторые постоянные параметры.

Формула Эйлера (8.3) представляет собой частный случай формулы (8.7) при 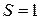, а формулы (8.6) – при .

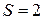Рассмотрим вопрос о выборе параметров 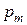, , 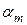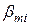. Для простоты ограничимся случаем 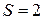. Введем обозначения

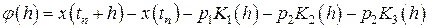. (8.9)

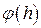– ошибка, которая имеет место на 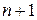шаге интегрирования для получения 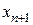при известном .

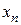Из выражения (8.7) следует, что

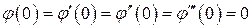. (8.10)

Учитывая соотношения (8.5), из равенства (8.9) имеем

,

,

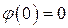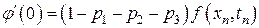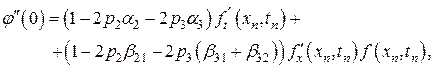
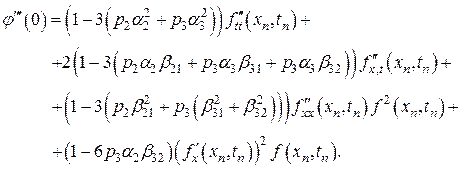
Приведенные выше условия (8.10) будут выполняться, если справедлива следующая система равенств

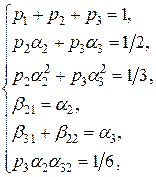
поскольку , , , , , .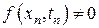

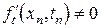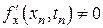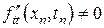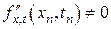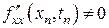Это – система из шести уравнений с восемью неизвестными, имеющая бесконечное множество решений. Наиболее употребительное решение системы (8.16)

, , ,

, ,

, , .

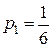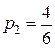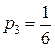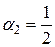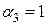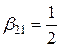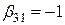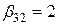Эти решения порождают следующие расчетные формулы

,

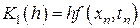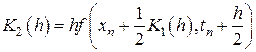, (8.11)

.

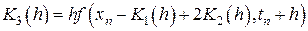Соответственно,

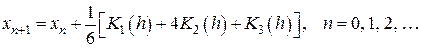. (8.12)

Вычислительная схема, реализуемая по формулам (8.11), (8.12) называется методом Рунге-Кутта 3-го порядка.

При 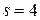получаем наиболее распространенную вычислительную схему метода Рунге-Кутта

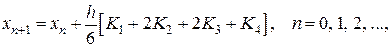(8.13)

где

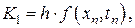
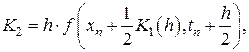
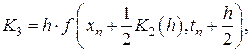
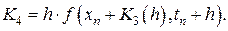
Еще раз отметим, что на каждом шаге интегрирования по методам Рунге-Кутта, согласно формуле (8.8) имеем локальную точность вычислений порядка .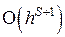

Рассмотренные методы интегрирования дифференциального уравнения являются одношаговыми. То есть для построения решения на следующем шаге необходимо знать информацию о значении решения только на предыдущем шаге.

Более быстродействующими являются многошаговые методы. Они используют информацию о поведении решения в нескольких предыдущих точках: 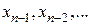.