Теория интегрирования Коши.

Примеры предыдущего пункта во-первых показывают существенное отличие интегрирования в комплексной области от интегрирования в действительной и во-вторых легко обобщаются.

Теорема Коши. Пусть 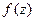− аналитическая функция в односвязной области D , а Г − любой кусочно – гладкий замкнутый контур, принадлежащий этой области. Тогда интеграл от функции f (z) по контуру Г равен нулю: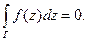

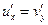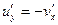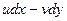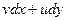Доказательство. Так как f − аналитическая функция, то ее действительная и мнимая части удовлетворяют условиям Коши – Римана: , , откуда сразу следует, что подынтегральные выражения и (п.2.1) представляют собой полные дифференциалы (см. ФНП) и, следовательно, соответствующие криволинейные интегралы по замкнутому контуру (см. ТП) равны нулю 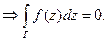(Пример 2.2 §10).

Доказанная теорема легко обобщается на многосвязные области.

Теорема. Пусть функция f (z) – аналитическая в многосвязной области 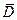, ограниченной ориентированным контуром Г. В этом случае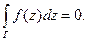

Доказательство (для двусвязной области (Рис.2)):

Область D ограничена контуром Г = Г₁ + Г₂ , ориентированным

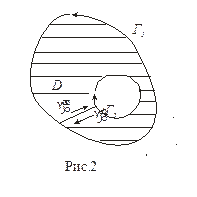в положительном направлении. Соединим контуры Г₁ и Г₂ линией γ. Ориентируем γ двумя способами: γ⁺ и γ⁻ . В результате получим односвязную область,

ограниченную контуром 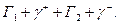По теореме Коши

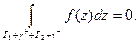Так как 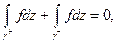получаем:

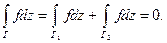В общем случае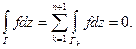

При этом, каждый из интегралов 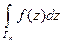может быть и не равным нулю.

Обозначим буквой Г кусочно – гладкий замкнутый контур, ориентированный против часовой стрелки, а тот же контур, ориентированный по часовой стрелке − символом Г ⁻ (в этих обозначениях в последней теореме следовало бы писать 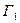и ).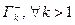

Следствие. Пусть область D ограничена внешним контуром Г и внутренними контурами

Г₁, … , Г_n . В последних обозначениях, для аналитической на 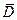функции имеет место

равенство: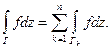

Доказательство.В указанных обозначениях утверждение теоремы имеет вид: 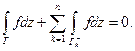Отсюда: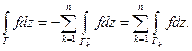

Замечание. Из полученных результатов следует, что примеры п.2.1 верны для любого кусочно – непрерывного замкнутого контура Г, содержащего точку z₀ : 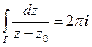и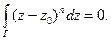

2.3 Формула Коши.

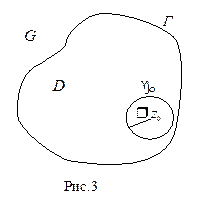Пусть функция f (z) является аналитической в односвязной области G, а z₀ – произвольная внутренняя точка этой области. Построим замкнутый контур Г 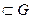и содержащий эту точку. Рассмотрим вспомогательную функцию 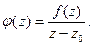Эта функция регулярна во всех точках области D ограниченной контуром Г, за исключением т. z₀. Проведем окружность γ с центром

в т. z₀ радиуса ρ, целиком принадлежащую области D. Если оба контура ориентировать против часовой стрелки, то будет иметь место равенство: 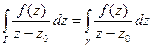(п.2.2). Так как левая часть равенства не зависит от ρ, то и правая от ρ не зависит. На контуре γ 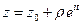и интеграл в правой части будет равен:

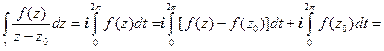
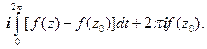
Подынтегральная функция в последнем интеграле стремится к нулю при 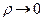, а сам интеграл от ρ не зависит. Отсюда сразу следует, что этот интеграл равен нулю (если предел постоянной – ноль , то постоянная равна нулю). Окончательно получаем формулу Коши:

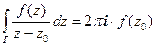(2.1)

Формулу Коши можно написать для произвольной точки 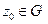, не принадлежащей контуру Г:

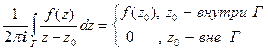
(равенство нулю сразу следует из теоремы Коши (п.2.2)).

Выражение, стоящее в левой части последней формулы, называют интегралом Коши.

2.4 Следствия интегральной формулы Коши.

Рассмотрим односвязную область G , ограниченную замкнутым контуром Г. Пусть задана функция 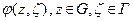, удовлетворяющая следующим условиям:

1. является аналитической функцией переменной z в области G.

2. Функции 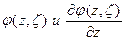непрерывны по совокупности переменных z и .

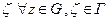В этом случае существует функция F(z) = 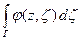как интеграл, зависящий от параметра z, определенная для .

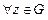Можно доказать, что при указанных предположениях F(z) является аналитической функцией

комплексной переменной z во всей области G , причем производную этой функции можно вычислять под знаком интеграла.

Рассмотрим теперь произвольную замкнутую подобласть 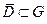, расстояние от всех точек которой до границы Г больше некоторого положительного числа d : 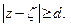Функция 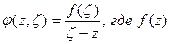− функция, аналитическая в области G , удовлетворяет условиям (1)

и (2) 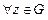. В свою очередь, функция f(z) во всех точках области D представляется

интегралом Коши: 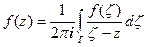(формула (2.1)). Пользуясь предыдущим утверждением, вычислим ее производную с помощью дифференцирования под знаком интеграла:

.

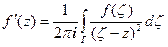Повторяя данные рассуждения, окончательно получим:

Аналитическая в области G функция бесконечно дифференцируема в этой области, а ее

производные удовлетворяют соотношению:

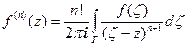или .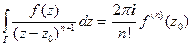

Полученные формулы часто используются при вычислении интегралов.

Пример. Вычислить интегралы: 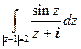и .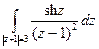

Решение. 1. Точка z = − i лежит внутри данной окружности, а функция 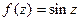, поэтому .

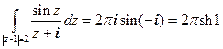2. .

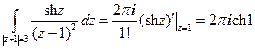Можно вычислять интегралы и в том случае, когда подынтегральная функция имеет несколько указанных особенностей в точках, лежащих внутри контура интегрирования, используя следствие теоремы Коши (§11). При этом необходимо учитывать, что регулярные части функции будут отличаться друг от друга в каждой особой точке.

Пример. .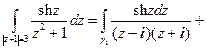

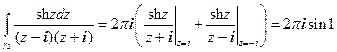2.5 Ряды Тейлора и Маклорена.

В п.1.6 были введены понятия рядов Тейлора и Маклорена функции f(z). Рассмотрим теперь более подробно свойства этих рядов. Для определенности, будем рассматривать только ряды Тейлора. Итак, пусть функция f(z) равна сумме некоторого степенного ряда в области его сходимости: 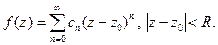Так как степенной ряд равномерно сходится в любом замкнутом круге 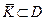(D − область сходимости) , то f(z) является непрерывной ,

бесконечно дифференцируемой функцией ( как сумма непрерывных и бесконечно дифференцируемых функций). Отсюда сразу следует, что f(z) − аналитическая функция в указанной области 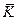. Имеет место и обратное утверждение:

Теорема Тейлора. Функция f(z) , аналитическая внутри круга 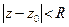, может быть однозначно представлена в этом круге сходящимся степенным рядом .

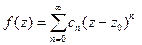Доказательство. Пусть z − произвольная внутренняя точка круга сходимости D. Построим окружность 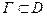с центром в т. z₀ , так, чтобы т. z лежала внутри этой окружности. По формуле Коши имеем: 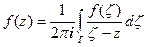(п.2.1). Представим подынтегральную функцию в виде ряда бесконечно убывающей геометрической прогрессии:

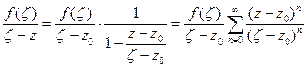
и проинтегрируем полученный ряд почленно (в силу равномерной сходимости ряда):

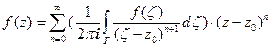. Используя следствие интегральной формулы Коши (п.2.4), полученный ряд можно написать следующим образом: .

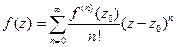Если предположить, что существует некоторый степенной ряд, сходящийся к той же функции:

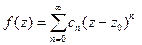, то последовательно дифференцируя это равенство, получим ,

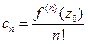что и доказывает единственность разложения.

Замечание. В действительной области бесконечной дифференцируемости функции недостаточно для разложимости в ряд Тейлора (f(x) = ехр(-1/х²)).

Пример. Написать разложение в ряд Маклорена функции 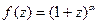и определить его радиус сходимости. Решение. Производная любого порядка в т. z = 0 легко вычисляется:

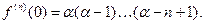Отсюда: 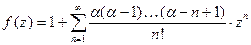. Радиус сходимости

находится по признаку Даламбера: 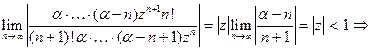R = 1.

(область сходимости обусловлена тем, что в т. z = 1 функция не является аналитической)

2.6 Ряды Лорана.

При исследовании функций комплексной переменной большую роль играют ряды по степеням

(z – z₀) более общего вида нежели рассмотренные ранее.

Определение.Рядом Лорана называется ряд .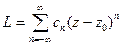

Т.е. суммируются все целые степени бинома (z – z₀). Поэтому ряды Лорана обычно

записывают следующим образом: 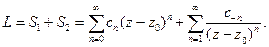Необходимым и

достаточным условием сходимости ряда Лорана является, очевидно, одновременная сходимость рядов S₁ и S₂ . Ряд S₁ представляет собой обычный степенной ряд (п. 1.6 ) и сходится в круге

радиуса R₁ c центром в т. z₀ : 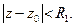Для исследования второго ряда ( S₂ ), сделаем замену переменных: 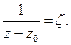Получившийся ряд 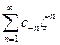является степенным рядом и сходится в

области 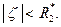Возвращаясь к исходной переменной, получим: 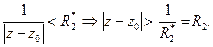Если R₂ > R₁ , то соответствующий ряд Лорана расходится во всех точках комплексной плоскости. Если же R₂ < R₁ , то областью сходимости будет кольцо

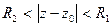. Имеет место следующая теорема:

Теорема.Функция f(z), аналитическая в круговом кольце 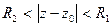, однозначно представляется в этом кольце сходящимся рядом Лорана. (б/д)

Пример. Найти все разложения функции 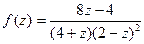по степеням z.

Решение. Представим функцию следующим образом:

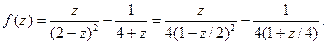
1) Каждое из слагаемых разложим в степенной ряд, пользуясь результатом примера §14:

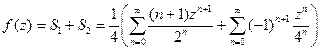. Ряд S₁ сходится в круге ,

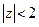ряд S₂ – в круге 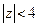. После несложных преобразований получаем:

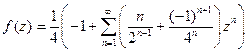− ряд Маклорена, сходящийся в круге .

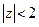2) Разложим функцию относительно бесконечно удаленной точки, сделав преобразование .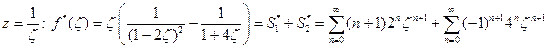

Область сходимости первого ряда 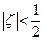, второго – 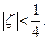Вернувшись к исходной

переменной, получим: 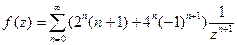− ряд Лорана, написанный только

по отрицательным степеням z , сходящийся в области .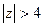

3) Если теперь сложить ряды 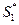и S₂ ( 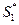равен первому, а S₂ − второму слагаемому исходной функции), то мы получим полный ряд Лорана, сходящийся в кольце :

.

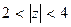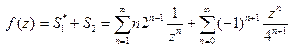Используя следствия интегральной формулы Коши (п.2.4), коэффициенты ряда Лорана могут быть представлены в интегральной форме. Для этого проведем две окружности С₁ и С₂ с центрами и т. z₀ , радиусы которых удовлетворяют условию 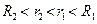. Тогда

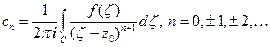, где С – произвольный замкнутый контур, лежащий

между окружностями С₁ и С₂ и содержащий т. z₀ .

2.7 Изолированные особые точки аналитической функции.

Определение. Точка z₀ называется изолированной особой точкой функции f(z) , если f(z) −

однозначная и аналитическая функция в круговом кольце 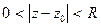, а т. z₀ является

особой точкой функции f(z). При этом, в самой т. z₀ функция может быть не определена.

По теореме предыдущего параграфа функция f(z) может быть представлена в данном кольце

сходящимся рядом Лорана. Возможны три случая:

1. В разложении функции нет слагаемых с отрицательными степенями.
2. Слагаемых с отрицательными степенями конечное число.
3. В разложении присутствует бесконечно много слагаемых с отрицательными степенями.

Рассмотрим каждый из этих случаев.

1) Ряд Лорана не содержит отрицательных степеней величины .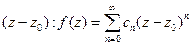

Можно доказать, что в этом случае существует предел 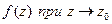равный с₀ . Если

доопределить (или переопределить) функцию в т. z₀ значением с₀ , то мы получим функцию, аналитическую в круге 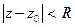. Поэтому особые точки рассмотренного вида называют

устранимыми особыми точками. Если разложение начинается с k-ой степени ( k > 0 ), то

точку z₀ называют нулемk-гопорядка функции f(z).

2) Ряд Лорана содержит конечное число отрицательных степеней: .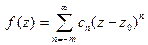

При выполнении указанного условия точку z₀ называют полюсом m-го порядка. Доказывается,

что предел аналитической функции при 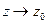в этом случае будет равен ∞.

Легко видеть, что функция 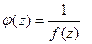в т. z₀ в первом случае будет иметь полюс k-го

порядка, а во втором – ноль m – го порядка.

3) Ряд Лорана содержит бесконечное число слагаемых членов разложения в отрицательных

степенях. Точка z₀ называется в этом случае существенно особой точкой функции f(z).

Поведение функции в окрестности существенно особой точки описывается теоремой:

Теорема.Для любого числа С и любого ε > 0 в любой окрестности z₀ найдется точка, значение функции в которой будет отличаться от С (по модулю) меньше чем на ε , т.е.:

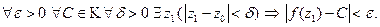(б/д)

Для всех сформулированных утверждений верны обратные. Поэтому часто используют геометрическую классификацию изолированных особых точек z₀:

Точка z₀ называется устранимой особой точкой, если существует конечный предел функции при 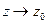. Ряд Лорана не содержит отрицательных степеней величины .

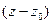Точка z₀ называется полюсом функции f(z), если 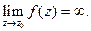Ряд Лорана содержит конечное число отрицательных степеней величины .

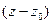Точка z₀ называется существенно особой точкой функции f(z), если при 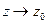предела не существует (конечного или бесконечного). Ряд Лорана содержит бесконечное число отрицательных степеней величины .

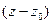2.8 Бесконечно удаленная особая точка.

Определение.Бесконечно удаленная точка комплексной плоскости называется изолированной особой точкойоднозначной аналитической функции f(z), если вне круга некоторого радиуса R,

т.е. при 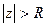, нет ни одной конечной особой точки функции f(z).

Для исследования функции в бесконечно удаленной точке сделаем замену 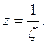Функция

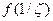будет иметь особенность в точке ζ = 0, причем эта точка будет изолированной, так как

внутри круга 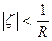других особых точек по условию нет. Являясь аналитической в этом

круге (за исключением т. ζ = 0 ), функция 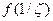может быть разложена в ряд Лорана по степеням ζ. Классификация, описанная в предыдущем параграфе полностью сохраняется.

Однако, если вернуться к исходной переменной z , то ряды по положительным и отрицательным степеням z ‘поменяются’ местами. Т.е. классификация бесконечно удаленных точек будет выглядеть следующим образом:

1) Ряд Лорана функции f(z) не имеет слагаемых с положительными степенями: 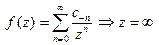− устранимая особая точка: 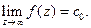Если, при этом, сумма начинается с n = m > 0, то z = ∞ ноль m−го порядка.

2) Ряд Лорана функции f(z) имеет конечное число слагаемых с положительными степенями: 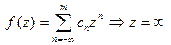− полюс m−го порядка: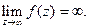

3) Ряд Лорана функции f(z) имеет бесконечное число слагаемых с положительными степенями: 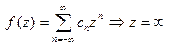существенно особая точка. Вне любого круга радиуса R функция f(z) принимает все комплексные значения.

Примеры. 1. 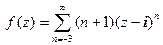. Точка z = i − полюс 3-го порядка.

2. 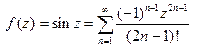. Точка z = ∞− существенно особая точка.