Примеры построения и решения многошаговых задач

Средствами динамического программирования

Планируется производство на 4 месяца. Необходимое число работников на каждый месяц известно: 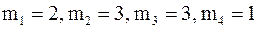. Перед началом работ 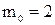. Допустим, что работа j-го месяца может быть выполнена меньшим числом работников. Пусть 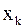- фактическое число работников в k-м месяце, где k=1,2,3,4. Затраты на изменение численности работников при переходе от (k-1)-го месяца к k-му определяются по формуле 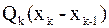и в зависимости от знака определяют найм или увольнение работника. В начальный момент 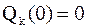. Отклонение от числа запланированных работников m_j приводит к дополнительным расходам 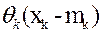. В начальный момент 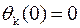. Необходимо найти такое число работников в каждом месяце x^j_k, чтобы затраты на отклонения от числа запланированных m_i были минимальными, где j=0,1…, 5- число возможных работников в k-м месяце.

Построение модели

1. Задача разбивается по месяцам на 4 шага ( k=1,2,3,4).

2. За состояние системы на k-м шаге x^j_k принимается число работников, в данном месяце, а за управление на k-м шаге - .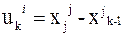

3. Устанавливается связь состояния x_k^j с предыдущим состоянием и с управлением в виде .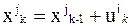

4. По данным предприятия записывается эффективность перехода в каждом k-м месяце

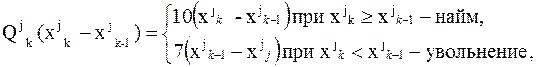
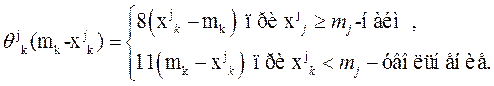
5. Общая целевая функция имеет вид .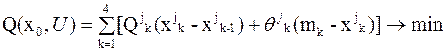

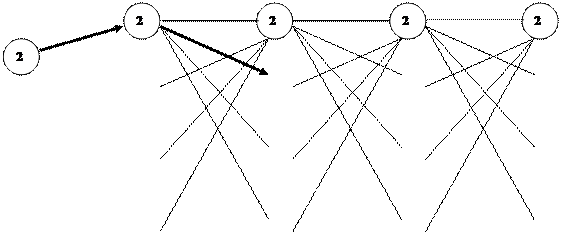
6. Строится граф задачи вида.

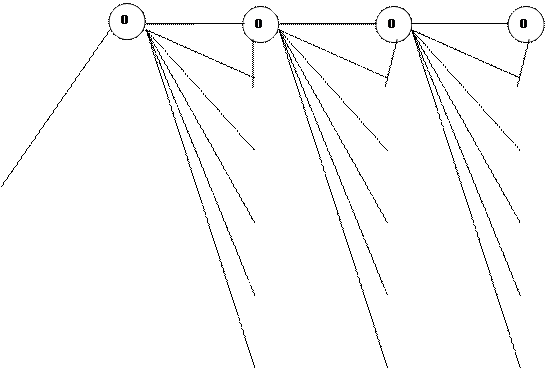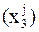U^j₁ U^j₂ U^j₃ U^j₄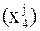

Решение задачи

1. Для поиска условного оптимума запишем уравнение Беллмана на

k-м и 4-м шагах:

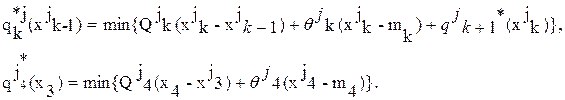
1. Определим условные оптимумы.

1. Определим условный оптимум на 4-м шаге 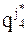. При этом варьируя переменными x^j₃ и x^j₄, составим таблицу.

x j3	x j4	qj4	Параметры, определяющие min q j4	u4
x3	x4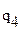
				1	0	0
						-1
						-2

Из таблицы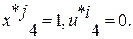

2. Определим условный оптимум на 3-м шаге 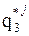. При этом принимая за оптимальное значение x ^j₄=1 и варьируя x ^j₂ и x ^j₃, составим таблицу.

x i2	x i3	qi3	Параметры, определяющие min qi3	u3
x2	x3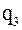
					18
				3	14	0
						-1

Из таблицы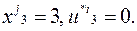

3. Определим условный оптимум на 2-м шаге 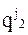. Принимая x ^j₄=1, x ^j₃=3 и варьируя x ^j₁ и x ^j₂, составим таблицу:

x j1	x j2	qj2	Параметры, определяющие min q j2	u2
x1	x2	q2
					46	+1
				4	32	0

Из таблицы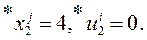

4. Определим условный оптимум на 1-м шаге q ^j ₁ .Т.к. x₀=2, варьируя x₁, составим таблицу:

x0	x1		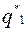u1
	2	46	0
			+1

Из таблицы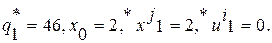

5. Построим ряд безусловных оптимумов:

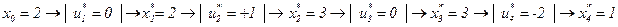Затраты Q(x₀,U)=q^*₁=46 .

Таким образом, для оптимального управления производством необходимо в 1-й месяц использовать нормативное число работников, на 2-м месяце - число работников увеличить на 1, на 3-м месяце - число работников

сохранить, на 4-м месяце - 2-х работников уволить. Первоначальный план позволял выполнить работу с затратами Q(x₀,U)=58 ед. налицо экономия в 12 ед.

Игровые задачи управления

Основы игровых задач

Математической основой игровых задач является теория игр, которая представляет собой дисциплину с предметом исследования принятия ре­шения в так называемых конфликтных ситуациях. Ситуация называется конфликтной, если в ней стал­киваются интересы нескольких (обычно двух) сторон, пре­следующих противоположные цели. Каждая из сторон может проводить ряд мероприятий для достижения своих целей, причем успех одной стороны означает неудачу другой.

Конфликтные ситуации часто возникают в экономике, когда при наличии свободной конкуренции в роли борющихся сторон выступают торговые фирмы, промышленные предприятия и т. п. К конфликтным ситуациям относятся почти все ситуа­ции, возникающие при планировании военных операций, выборе системы оружия, охране объектов от нападения, преследовании и перехвате цели и т. п., спортивные со­стязания, арбитражные споры, аукционы, выборы в пар­ламент при наличии нескольких кандидатов на одно ме­сто.

Для того чтобы сделать возмож­ным математический анализ конфликтной ситуации, ее необходимо упростить, учтя только основные факторы. Упрощенная формализованная модель конфликтной си­туации называется игрой, а конфликтующие стороны— игроками.

Рассмотрим игры, в кото­рых имеется только две конфликтующие стороны. Игра представляет собой со­вокупность правил, описывающих поведение игроков.

Понятие стратегии

Представим себе, что мы хотим сыграть шахмат­ную партию белыми, но лично присутствовать при игре не можем. У нас есть заместитель, который должен про­вести партию и выполнять все наши указания. Но сам он не способен принимать самостоятельные решения. Чтобы заместитель мог про­вести всю партию до конца, ему должны быть даны та­кие указания, которые предусматривали бы любые воз­можные положения на доске и для каждого положения определяли бы тот ход, который должен быть сделан. Полная система таких указаний и представляет собой стратегию.

Так, стратегия белых должна указывать первый ход, затем для каждого возможного ответа черных следую­щий ход белых и т. д. Конечно, составление полной стра­тегии при игре в шахматы является огромной, практиче­ски невыполнимой работой. Например, игрок белыми, присутствующий лично, должен принять два решения, чтобы сделать два первых хода. Играя же через замести­теля, он должен подготовить 21 решение для тех же двух ходов (одно решение — первый ход и 20 решений — от­веты на 20 возможных первых ходов черных). Тем не менее, во многих более простых задачах понятие страте­гии является весьма полезным.

Таким образом, стратегия игрока представляет собой однозначное описание его выбора в каждой возможной ситуации, при которой он должен сделать личный ход.

Если игра состоит только из личных ходов, то исход игры определен, если каждый из игроков выбрал свою стратегию. Однако, если в игре имеются случайные хо­ды, то игра будет носить вероятностный характер и вы­бор стратегий игроков еще не определит окончательно исход игры.

Обозначим через X и У множество или простран­ство всевозможных стратегий, которыми могут пользо­ваться участники игры, называемые далее первым и вторым игроками соответственно. Величины 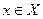и 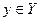будут означать конкретные стратегии первого и второго игроков.

Для того чтобы ввести в рассмотрение случайные ходы, удобно считать, что в игре принимает участие условно третий игрок, который и делает случайные ходы, поль­зуясь для этого соответствующим механизмом случайно­го выбора. Обозначим через H пространство стратегий этого игрока. Любая стратегия 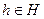третьего игрока, представляющая собой конкретную последовательность всех случайных ходов в партии, будет происходить с не­которой вероятностью p(h), которую легко подсчитать, зная вероятности каждого случайного хода в этой после­довательности. Легко видеть, что p(h) представляет со­бой распределение вероятностей на пространстве H, т. е. удовлетворяет условиям

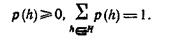
Обозначим через g некоторый вариант игры, т. е. одну возможную партию. Этот вариант будет определен, если выбраны стратегии игроков х и у и стратегии слу­чайных ходов h. Следовательно, конкретная партия g представляет собой тройку величин х, у и h:

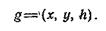
Результатом партии является выигрыш или проигрыш каждого из игроков. Для удобства выигрыши и проигры­ши будем оценивать каким-либо числом, например сум­мой денег в рублях.

Рассмотрим одну из конкретных партий g(x, y, h) и обозначим через L_x(x, у, h) и L_у(х, у, h) проигрыши или потери первого и второго игроков соответственно. При этом выигрыши рассматриваем как отрицательные про­игрыши. Общая сумма проигрышей обоих игроков рав­на:

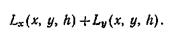
В дальнейшем ограничимся рассмотрением только так называемых игр с нулевой суммой. В та­ких играх проигрыш одного игрока равен выигрышу другого игрока.

При рассмотрении игр с нулевой суммой нет необхо­димости отдельно учитывать проигрыши или выигрыши обоих игроков, а можно ограничиться рассмотрением только проигрыша второго игрока (выигрыша первого игрока):

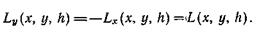
Поскольку стратегия h является случайной, то при выбранных стратегиях х и у потери L(x, у, h) будет слу­чайной величиной с распределением вероятностей p(h) на пространстве Н. Поэтому оценить выбранные страте­гии х и у можно лишь путем усреднения потерь L(x, у, h) по всему пространству H, т. е. введя понятие средних потерь L(x, у), определяемых из соот­ношения

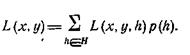
Игра будет определена, если перечислены все воз­можные стратегии игроков, т. е. заданы пространства X , и Y, и для любых 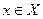и 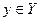определены потери L(x,у). Игра G определяется тройкой

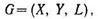
где X и Y представляет собой некоторые пространства, a L — ограниченная числовая функция. Точк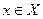и и 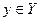назы­ваются стратегиями первого и второго игроков, а функ­ция L называется функцией потерь.

Игры, в которых каждый игрок имеет конечное число стратегий (конечные игры), удобно задавать в виде так называемой матрицы потерь. Пусть G=(X, Y, L)—ко­нечная игра, в которой Х={х₁ ..., x_m} и Y={у₁ ..., у_m}. Тогда матрица порядка m´п

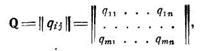
в которой q_ij = L(x_i,y_j) называется матрицей игры G.

Для того чтобы описание игры было законченным, необходимо указать цели, которыми руководствуются игроки при выборе своих стратегий. Эти цели достаточно просты. Первый игрок стремится обеспечить себе наибольший выигрыш, т. е. максимизировать функцию L(x, у), а второй игрок стремится сделать свой проиг­рыш наименьшим, т.е. минимизировать функцию L(x, у). Специфической трудностью при этом является то, что ни один из игроков не контролирует полностью значение L(x, у), так как первый игрок распоряжается только значением х, а второй — только зна­чением у.