Увеличение энтропии при теплопередаче
 Если привести в соприкосновение два тела А и В, температуры которых равны ТА и ТВ, то теплота будет переходить от более нагретого тела к менее нагретому, в результате чего температуры обоих тел выравниваются. Пусть ТА>ТВ (рис.5).
Если привести в соприкосновение два тела А и В, температуры которых равны ТА и ТВ, то теплота будет переходить от более нагретого тела к менее нагретому, в результате чего температуры обоих тел выравниваются. Пусть ТА>ТВ (рис.5).
Состояние тела A изменяется за счёт потери тепла –dQ, а состояние тела B за счёт приобретения такого же количества тепла dQ. Для определения изменения энтропии системы состоящей из обоих тел, нужно вычислить 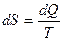 для какого-нибудь обратимого процесса, приводящего к тому же изменению состояния. Таким процессом может служить процесс передачи тепла от A к B при помощи третьего тела. Тогда для тела А
для какого-нибудь обратимого процесса, приводящего к тому же изменению состояния. Таким процессом может служить процесс передачи тепла от A к B при помощи третьего тела. Тогда для тела А
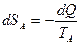 ,
,
а для тела В
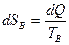 .
.
 Общее изменение энтропии обоих тел равно
Общее изменение энтропии обоих тел равно
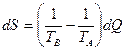 .
.
Так как ТА>TB, то dS>0, т.е. энтропия системы возрастает.
Можно вообще показать, что любые необратимые процессы в замкнутой системе сопровождаются возрастанием энтропии.
Пусть некоторая система само собой, т.е. необратимым путем, переходит из состояния А в состояние В. Вернем теперь эту систему в начальное состояние А обратимым путем. Взятые вместе оба процесса образуют круговой процесс, причем процесс необратимый. Для необратимого процесса
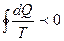 .
.
Если представить этот интеграл как сумму двух интегралов, соответствующих двум стадиям кругового процесса, то получим
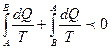 .
.
Первый из этих интегралов равен нулю, так как система замкнутая и теплота не поглощалась и не выделялась системой. Второй же интеграл, поскольку он относится к обратимому процессу, равен
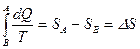 ,
,
следовательно
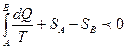
и
SA-SB<0
или
SA<SB,
т.е. энтропия при необратимом переходе из одного состояния в другое возрастает.
Энтропия и вероятность
 Необратимость тепловых процессов связана с тем, что переход к равновесному состоянию является подавляюще более вероятным по сравнению с другими переходами. Бросается в глаза сходство поведения обоих величин энтропии и вероятности, обе они растут пре переходе к равновесию. Естественно связать энтропию системы в том или ином состоянии с вероятностью этого состояния. Для этого более точно определим понятие вероятности состояния. Для этого рассмотрим распределение частиц газа в объёме сосуда. Представим себе сосуд, разделённый на 2 части (рис.6). Пусть в этом сосуде находится 6 молекул, каждой из которых мы припишем определённый номер. Эти 6 молекул могут быть размещены в обеих половинах сосуда 64 различными способами. Каждому из них соответствует определённое состояние системы. Состояние, при котором в левой части находиться одна молекула, в правой части –5 отличается от состояния, когда в левой части находится 2, а в правой 4. Рассмотрим, сколькими из общего числа способов размещения молекул осуществляется каждое состояние системы. Лишь одно размещение создаёт такое состояние, в котором в левой части молекул вовсе нет. Состояние слева 1, справа 5 молекул определяется 6 способами, слева 2, справа 4 – 15 способами. Наибольшее число способов размещения определяет такое состояние, при котором слева и справа окажутся по 3 молекул, т.е. равномерное распределение молекул между обеими половинами сосуда.
Необратимость тепловых процессов связана с тем, что переход к равновесному состоянию является подавляюще более вероятным по сравнению с другими переходами. Бросается в глаза сходство поведения обоих величин энтропии и вероятности, обе они растут пре переходе к равновесию. Естественно связать энтропию системы в том или ином состоянии с вероятностью этого состояния. Для этого более точно определим понятие вероятности состояния. Для этого рассмотрим распределение частиц газа в объёме сосуда. Представим себе сосуд, разделённый на 2 части (рис.6). Пусть в этом сосуде находится 6 молекул, каждой из которых мы припишем определённый номер. Эти 6 молекул могут быть размещены в обеих половинах сосуда 64 различными способами. Каждому из них соответствует определённое состояние системы. Состояние, при котором в левой части находиться одна молекула, в правой части –5 отличается от состояния, когда в левой части находится 2, а в правой 4. Рассмотрим, сколькими из общего числа способов размещения молекул осуществляется каждое состояние системы. Лишь одно размещение создаёт такое состояние, в котором в левой части молекул вовсе нет. Состояние слева 1, справа 5 молекул определяется 6 способами, слева 2, справа 4 – 15 способами. Наибольшее число способов размещения определяет такое состояние, при котором слева и справа окажутся по 3 молекул, т.е. равномерное распределение молекул между обеими половинами сосуда.
Можно показать, что если в сосуде имеется N молекул и они нумерованы, то между двумя половинами сосуда их можно разделять 2N способами. Из этого числа размещений число Z размещений, при которых в одной половине находиться n молекул, а в другой N – n молекул определяется равенством
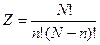 .
.
При любом N значении Z будет наибольшим при n=N/2, т.е. наибольшим числом способов осуществляется равномерное распределение молекул в объеме сосуда. Этот же результат будет, если сосуд делить не на 2, а на произвольное число частей.
Перейдём к вероятности того или иного распределения частиц между обеими половинами сосуда. Вообще вероятность W того, что в левой части находится n из N частиц равна
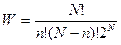 .
.
При большем числе частиц N, число способов, которым осуществляется равномерное распределение частиц в объёме сосуда, может намного больше, чем неравномерное распределение. В результате хаотичного движения молекул газ может находиться в любом из мыслимых состояний, но в подавляюще большем числе случаев мы найдём его в состоянии, которое осуществляется наибольшим числом размещений, т.е. в состоянии равномерного распределения, это состояние является равновесным.
Таким образом, каждое состояние можно характеризовать не только математической вероятностью
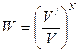 ,
,
но и числом способов, которым это состояние осуществляется. Эта величина 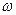 равная числу размещений Z называется термодинамической вероятностью. В отличие от математической вероятности, термодинамическая вероятность больше единицы.
равная числу размещений Z называется термодинамической вероятностью. В отличие от математической вероятности, термодинамическая вероятность больше единицы.
С величиной термодинамической вероятности может быть связана энтропия, так как и та и другая имеют максимальное значение в состоянии равновесия и переход всякой системы к равновесному состоянию сопровождается ростом энтропии и термодинамической вероятности. Больцман связал энтропию S и термодинамическую вероятность W соотношением
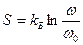
или
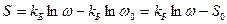 ,
,
где
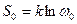 .
.
Если S0 принять за начало отчёта, то 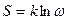 .Связь между энтропией и вероятностью позволяет несколько иначе трактовать II начало термодинамики. Оно теперь означает, что всякий процесс в природе протекает так, что система переходит в состояние с большей вероятностью. Но это не означает, что переход в другие состояния невозможны, но переход к равновесию лишь более вероятен, чем самопроизвольное удаление от равновесия системы. Второе начало термодинамики надо понимать так, что если система находится в состоянии с данной энтропией, то с подавляющей вероятностью следует ожидать, что оно перейдёт в состояние с большей энтропией, т. е. наиболее вероятным изменением энтропии является её возрастание. Принципиально же мыслимы и процессы, сопровождающиеся уменьшением энтропии, но их вероятность мала.
.Связь между энтропией и вероятностью позволяет несколько иначе трактовать II начало термодинамики. Оно теперь означает, что всякий процесс в природе протекает так, что система переходит в состояние с большей вероятностью. Но это не означает, что переход в другие состояния невозможны, но переход к равновесию лишь более вероятен, чем самопроизвольное удаление от равновесия системы. Второе начало термодинамики надо понимать так, что если система находится в состоянии с данной энтропией, то с подавляющей вероятностью следует ожидать, что оно перейдёт в состояние с большей энтропией, т. е. наиболее вероятным изменением энтропии является её возрастание. Принципиально же мыслимы и процессы, сопровождающиеся уменьшением энтропии, но их вероятность мала.
Энтропия и беспорядок
Тепловая энергия тела – это энергия хаотичного, беспорядочного движения его молекул. Этой хаотичностью тепловое движение молекул отличается от макроскопического механического движения тела, при котором составляющие его молекулы движутся упорядоченно, причем упорядоченное движение накладывается на хаотичное движение молекул. Превращение тепловой энергии в механическую сводится к превращению хаотичного теплового движения молекул в движение упорядоченное.
Преобразовать механическую энергию в тепловую это значит, превратить энергию порядка в энергию беспорядка. Это два обратных процесса неравноправные: превратить упорядоченное движение в хаотическое несравненно легче, чем производить обратное превращение.
Всякий естественный процесс всегда протекает так, что система переходит в состояние с большим беспорядком: температура сама собой выравнивается, газ сам перемешивается.
Сходство между степенью беспорядка системы и энтропией очевидно. Естественно считать энтропию мерой беспорядка системы, имея в виду связь между энтропией и вероятностью состояния. Можно сказать, что состояние с большим беспорядком характеризуется большей термодинамической вероятностью, чем более упорядоченная система. Этим связана необратимость тепловых процессов: они протекают так, что беспорядок в системе увеличивается.
Необратимость тепловых процессов – это необратимость порядка и беспорядка. Этим связан и тот факт, что любой вид энергии, в конце концов, переходит в тепло, так как тепловая энергия – это энергия беспорядочных движений, в то время как другие виды энергии связаны с более упорядоченным движением.
Обобщая все сказанное выше, сформулируем основные свойства энтропии:
