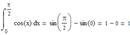Основные свойства определенных интегралов
Первообразная функция. Понятие неопределенного интеграла.
Опр.1 Если  (x)=f(x) на множестве x, для любого X, то F(x)-называется первообразной функции f(x). Лемма: Если f(x), равняется 0 на некотором интервале, то F(x)=C на этом интервале. Теорема: Если F(x) - первообразная для f(x) на X, а
(x)=f(x) на множестве x, для любого X, то F(x)-называется первообразной функции f(x). Лемма: Если f(x), равняется 0 на некотором интервале, то F(x)=C на этом интервале. Теорема: Если F(x) - первообразная для f(x) на X, а 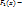 другая первообразная, то
другая первообразная, то 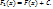
Опр.2.Множество всех первообразных функции, называется неопределенным интегралом.
Оснновные свойства неопределенных интегралов.
А) 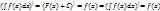 .
.
Б) 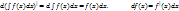
В) 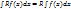
Г) 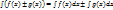 .
.
Таблица основных интегралов.
1) 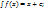
2) 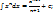
3) 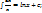
4) 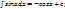
5) 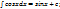
6) 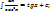
7) 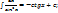
8) 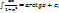
9) 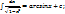
10) 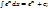
11) 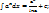
12) 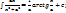
13) 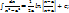
14) 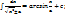
15) 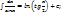
16) 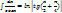 +c;
+c;
17) 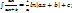
Непосредственное интегрирование.
Использование свойств интеграла и таблицы.
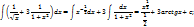
Метод подстановки
Замена под знаком интеграла.
Теорема: Если 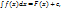 то
то 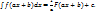
Док-во. 
Пример: 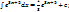
Метод интегрирования по частям. Циклические интегралы.
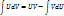
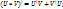
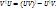
Если существует первообразная для UV и V  , то существует интеграл
, то существует интеграл 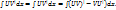
Циклические интегралы: 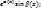
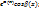
( 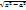 ;
; 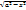 ) – принимаются за U.
) – принимаются за U.
Интегрирование рациональных дробей.
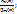 P и Q – многочлен, причем n – старшая степень, m – это старшая степень знаменателя.
P и Q – многочлен, причем n – старшая степень, m – это старшая степень знаменателя. 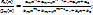 Опр.1.Если n
Опр.1.Если n 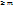 , то дробь называется неправильной, необходимо поделить числитель на знаменатель и выделить целую часть.
, то дробь называется неправильной, необходимо поделить числитель на знаменатель и выделить целую часть.
Существует теорема, утверждающая, что любой многочлен можно представить в виде:  где:
где: 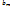 - главный коэффициент при Х;
- главный коэффициент при Х; 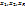 - корни многочлена;
- корни многочлена; 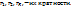 Опр.2. Если n<m, то дробь правильная. Для того, чтобы проинтегрировать правильную дробь, многочлен в знаменателе раскладывают на множители. После чего, подынтегральную функцию раскладывают на элементарные дроби, для этого используют метод неопределенных коэффициентов.
Опр.2. Если n<m, то дробь правильная. Для того, чтобы проинтегрировать правильную дробь, многочлен в знаменателе раскладывают на множители. После чего, подынтегральную функцию раскладывают на элементарные дроби, для этого используют метод неопределенных коэффициентов.
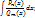
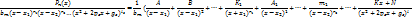
Интегрирование тригонометрических функций.
I.
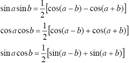
II.
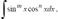
где m и n - четные числа находятся с помощью формул понижения степени:
III. Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
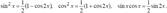

Примеры:
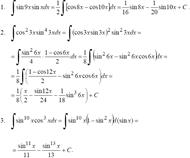
IV. 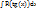 или
или 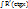 dx
dx
Замена : tgx=t или ctgx=t
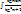 =
= 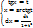 =
= 
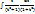 =
= 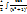 =
= 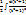 =
= 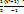 + C = -
+ C = - 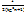 + C
+ C
V. Универсальная тригонометрическая подстановка.
sinx = 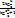 , cosx =
, cosx = 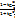 , подстановка
, подстановка 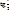 = t
= t
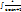 dx =
dx = 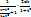 =
= 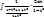 = t+C = tg
= t+C = tg 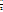 +C
+C
VI.
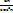 ,
, 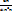
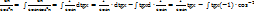 (2)
(2) 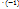 sinxdx =
sinxdx = 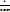 tgx =
tgx = 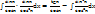 =
= 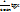 –
– 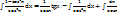
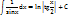
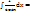
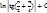
I = 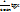 – I +
– I + 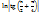
2I = 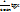 +
+ 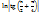
I = 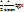 +
+ 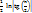
Интегрирование иррациональных уравнений.
I. 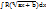 , замена “a”: ax+b-
, замена “a”: ax+b- 
Пример:
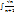 dx =
dx = 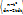 =
= 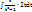 =
= 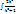 dt = 2
dt = 2 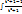 dt = 2
dt = 2 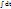 - 2
- 2 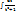 = 2t – 2arc
= 2t – 2arc  + C = 2
+ C = 2 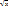 - 2arctg
- 2arctg 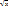 +C
+C
II. 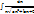 , замена:
, замена: 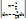
или
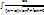 , замена:
, замена: 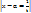 , dx = -
, dx = - 
Пример:
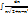 =
= 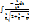 =
= 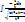 =
= 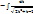 = -
= - 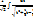 = -
= - 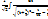 = -
= - 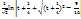 = -
= - 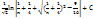
Тригонометрические подстановки в иррациональных интегралах.
III. 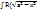 )dx
)dx
Замена: x=a  sint, dx=a
sint, dx=a  costdt
costdt
Пример:
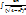 =
= 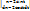 =
= 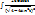 =
= 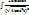 =
= 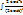 dt =
dt = 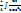 =
= 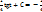 tg(arcsin
tg(arcsin 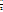 ) + C
) + C
IV. 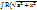 )dx
)dx
Замена: x=a  tgt, dx =
tgt, dx = 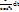
V. 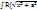 )dx
)dx
Замена: x= 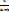 , dx= -
, dx= - 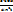 dt
dt
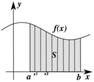
Понятие определенного интеграла.
Определённый интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
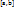 разбиваем на n произвольных одинаковых отрезков длиной
разбиваем на n произвольных одинаковых отрезков длиной 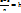 , получаем точки на оси 0x:
, получаем точки на оси 0x:  ,
,  ,
,  ,
,  , …,
, …, 
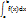
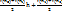 h+
h+ 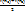 h+… =
h+… =  (f(
(f(  )+2
)+2 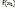 +
+ 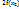 +…+2f(
+…+2f( 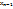 )+2f(
)+2f(  )) =
)) = 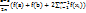
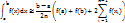
Основные свойства определенных интегралов.
Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то:
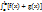 dx =
dx = 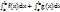 ,
,
т. е. интеграл суммы равен сумме интегралов слагаемых.
Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то:
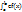 dx=c
dx=c 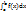 ,
,
т. е. постоянный множитель можно выносить за знак интеграла.
Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
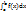 =
= 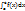 +
+ 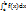 , (a<c<b).
, (a<c<b).
Теорема 4. Если f(x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего, то и сам интеграл будет числом неотрицательным:
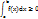
Среднее значение функции.
Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями. Наиболее важной теоремой о среднем значении функции в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если f(x) непрерывна на отрезке [a,b] и дифференцируема в интервале (a,b) , то существует точка “c”, принадлежащая интервалу (a,b) , такая, что f(b) – f(a) = (b-a)  (c).
(c).
В интегральном исчислении наиболее важной теоремой о среднем значении является следующая: если f(x) непрерывна на отрезке [a,b], a  (x) сохраняет постоянный знак, то существует точка “c” из интервала (a,b) такая, что
(x) сохраняет постоянный знак, то существует точка “c” из интервала (a,b) такая, что
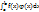 = f(c)
= f(c) 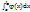
В частности, если 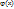 =1, то
=1, то
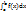 =f(c)(b-a)
=f(c)(b-a)
Вследствие этого под средним значением функции f(x) на отрезке [a,b] обычно понимают величину:
 =
= 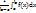
Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
Формула Ньютона-Лейбница.
Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедливо равенство 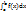 =F(b)-F(a) - основная формула интегрального исчисления.
=F(b)-F(a) - основная формула интегрального исчисления.
Благодаря формуле Ньютона-Лейбница устанавливается связь между определенным и неопределенным интегралом. А именно:
Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница.
Пример: