Определители второго и третьего порядков

Определителем квадратной матрицы второго порядка

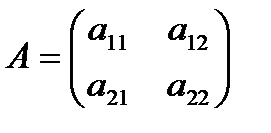
называется число, равное произведению элементов на главной диагонали матрицы минус произведение элементов на побочной диагонали, т.е.

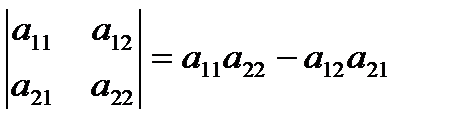(3)

Например, .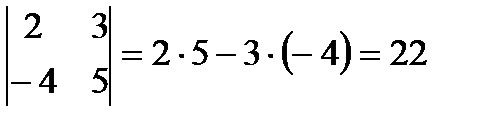

Определителем квадратной матрицы третьего порядка 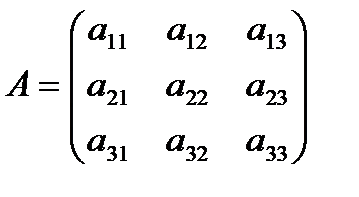называется число

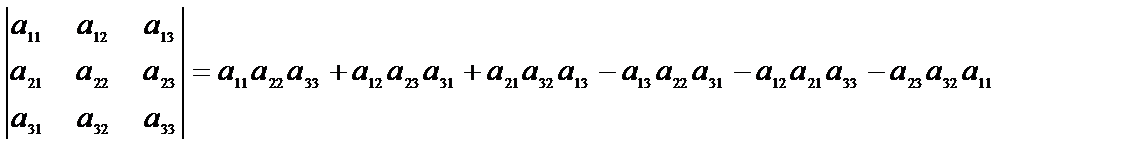(4)

Запомнить формулу (4) легко в виде так называемого правила треугольников. В соответствии с ним со знаком "плюс" берутся произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали. Члены со знаком "минус" определяются аналогично, но относительно побочной диагонали.

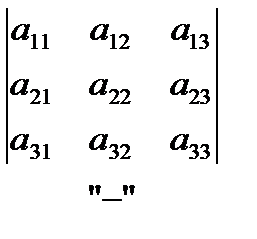
Пример. Вычислить определитель матрицы 3-го порядка

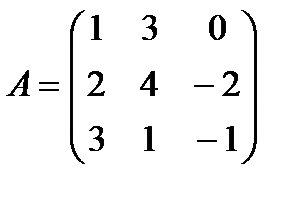
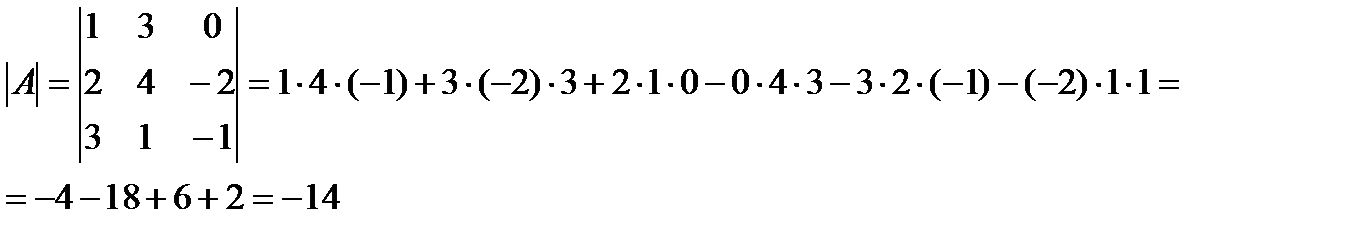
Определители n-го порядка.

Перейдем к выяснению понятия определителя любого порядка n, где n³3.

Рассмотрим квадратную матрицу n-го порядка

.

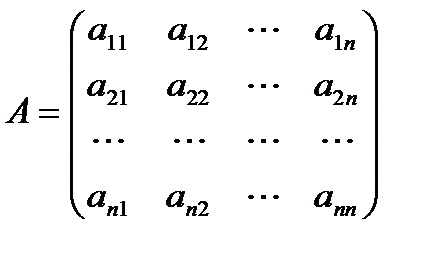Минором М_ij элемента а_ij определителя n-го порядка называется определитель (n-1)-го порядка, получающийся из данного определителя вычеркиванием i-й строки и j- го столбца (строки и столбца, в которых стоит элемент).

Алгебраическим дополнением А_ij элемента а_ij называется число, равное 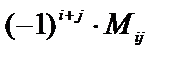, т.е.

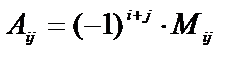(5)

где i - номер строки, в которой стоит элемент а_ij,

j - номер столбца.

Из формулы (3.3) следует, что алгебраическое дополнение А_ij отличается от отвечающего ему минора М_ij только знаком, т.е. А_ij = M_ij или А_ij =-M_ij в зависимости от четности или нечетности суммы индексов (i+j).

Пример. Пусть 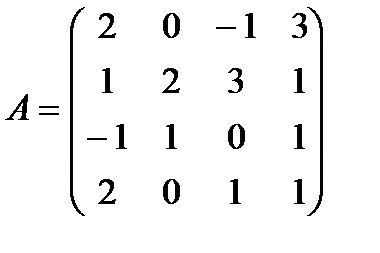. Найти М₂₁, А₂₁, М₃₃, А₃₃.

Решение.

.

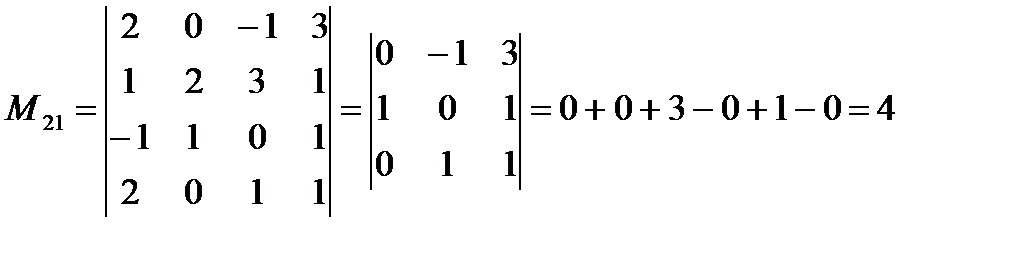
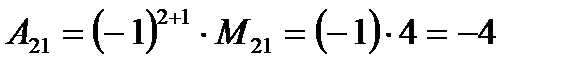
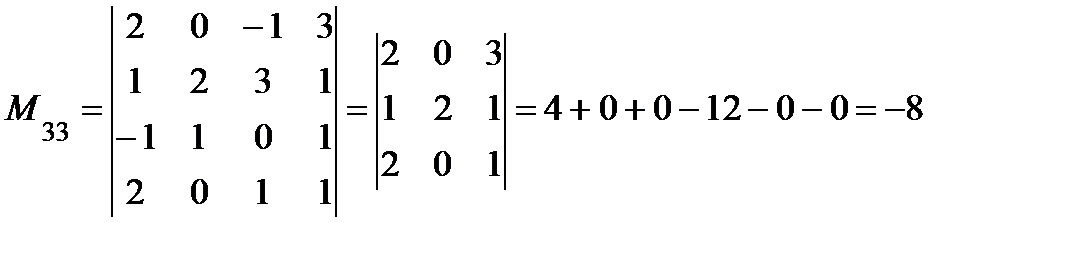
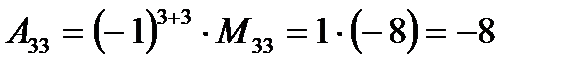Определитель n-го порядка равен сумме произведений элементов первой строки определителя на их алгебраические дополнения

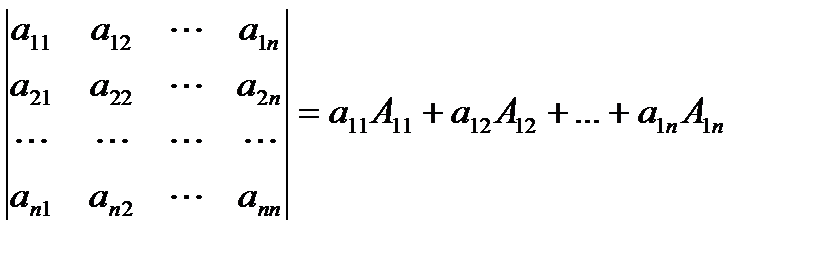(6)

Такое представление определителя называют разложением определителя по первой строке. Оказывается, разлагать определитель можно не только по первой, но и по любой другой строке, а также по любому столбцу определителя:

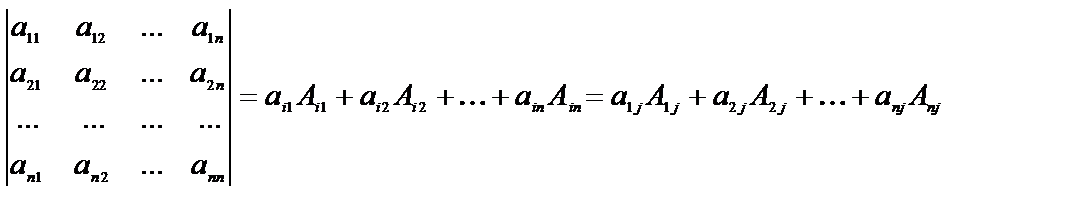(7)

где i - любое из чисел 1,2,…,n,

j - любое из чисел 1,2,…,n.

Операция разложения определителя n- го порядка по строке (столбцу) позволяет свести его значение к вычислению n определителей, но уже меньшего (n-1)-го порядка.

Пример. Вычислить определитель матрицы

.

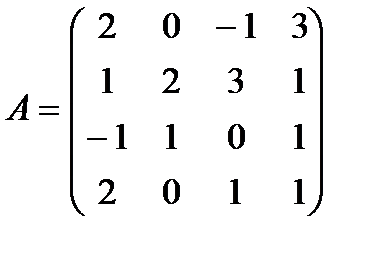Решение.

Вычислим определитель, разложив его по четвертой строке

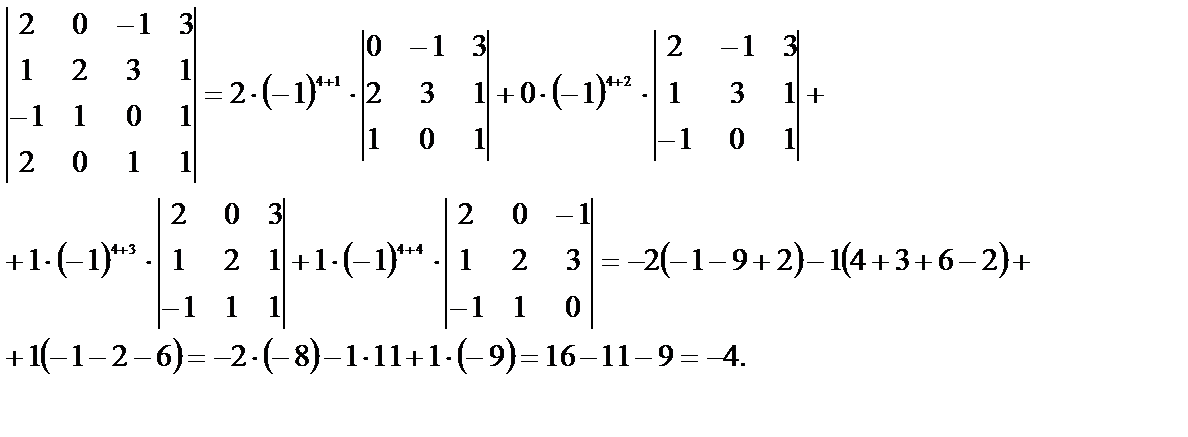
Наличие одного нуля в строке, по которой производилось разложение, избавило нас от необходимости вычислять один определитель третьего порядка. Поэтому, если бы в определителе можно было получать нули, не изменяя значение определителя, число необходимых вычислений значительно бы сократилось. Возможность тех или иных преобразований элементов определителя зависит от свойств определителей.

Свойства определителей.

Свойство 1. При транспонировании квадратной матрицы ее определитель не меняется, т.е. .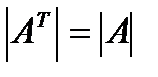

Свойство 2. При перестановке двух строк (двух столбцов) определитель меняет знак.

Свойство 3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

Свойство 4. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя:

Свойство 5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.

Свойство 6. Определитель, элементы двух строк (двух столбцов) которого пропорциональны, равен нулю.

Свойство 7. Если в определителе все элементы некоторой строки (некоторого столбца) представляют сумму двух слагаемых, то такой определитель равен сумме двух определителей: у одного элементами соответствующей строки являются первые слагаемые, у второго – вторые, а остальные строки во всех трех определителях одинаковые.

Свойство 8. Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель α, то величина определителя не изменится, т.е.

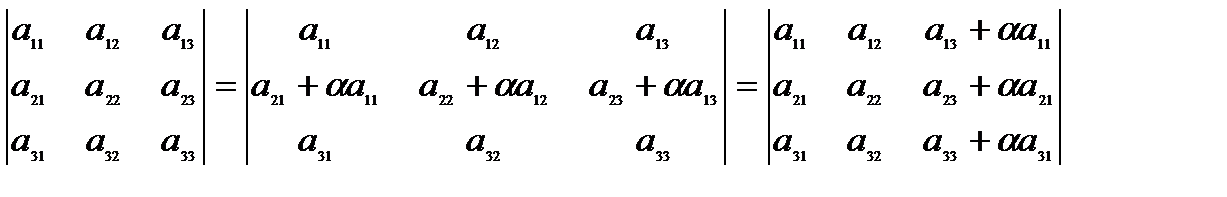
Свойство 8 является основным свойством, используемым для преобразования элементов определителя без изменения его величины и, в частности, для получения нулей в строке или столбце определителя.

Замечание. Значение определителя изменится, если строку (столбец) умножить на произвольный множитель α и прибавить к ней другую строку (столбец).

Пример 1.Вычислить определитель второго порядка .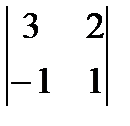

Решение. .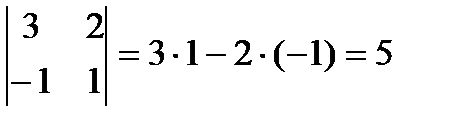

Пример 2.Вычислить определитель третьего порядка .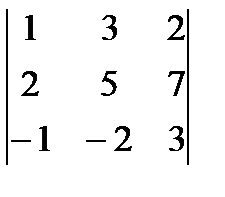

Решение.

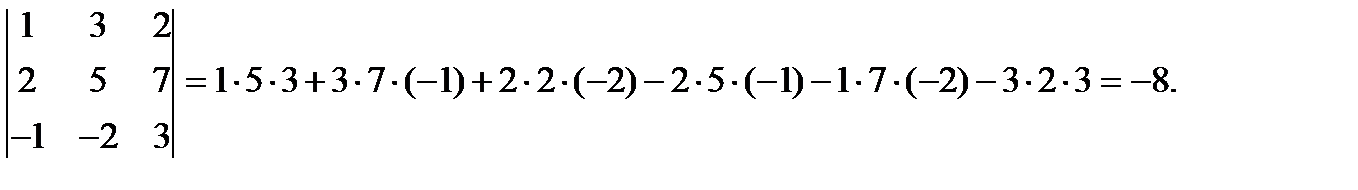
Вычислим этот же определитель, используя разложение определителя по элементам какой-либо строки или столбца. Так как раскладывать определитель можно по элементам любой строки или столбца, то целесообразно выбрать строку или столбец, содержащих больше нулей. А для этого преобразуем наш определитель так, чтобы в некоторой строке (столбце) часть элементов обратилась в нуль. Пусть мы хотим получить нули в первом столбце. Для этого выберем строку, которая в первом столбце имеет 1 или -1 и перепишем ее без изменения. Итак, оставим без изменения, например, первую строку (т.е. выберем ее в качестве рабочей). Умножив все ее элементы на (-2) и прибавив их к соответствующим элементам второй строки, получим ноль на месте элемента 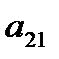. Аналогично, сложив первую строку с третьей, получим ноль на месте элемента :

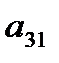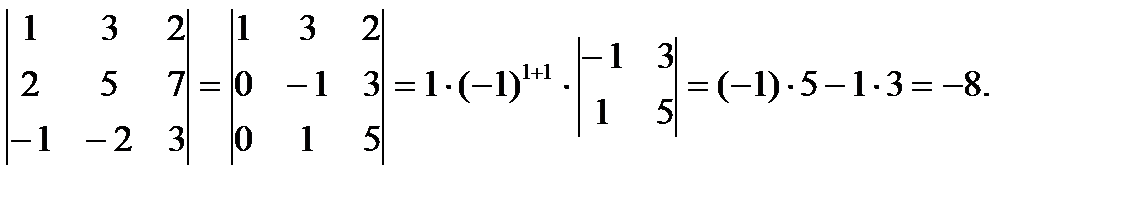
Замечание. Если нули хотят получить в столбце, то в качестве рабочей должна выступать некоторая строка, если же нули получают в какой-либо строке, то в качестве рабочего должен выступать некоторый столбец.

Пример 3.Вычислить определитель четвертого порядка

.

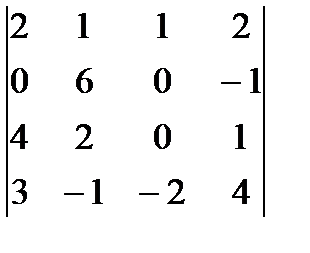Решение. Разложим определитель по элементам второй строки.

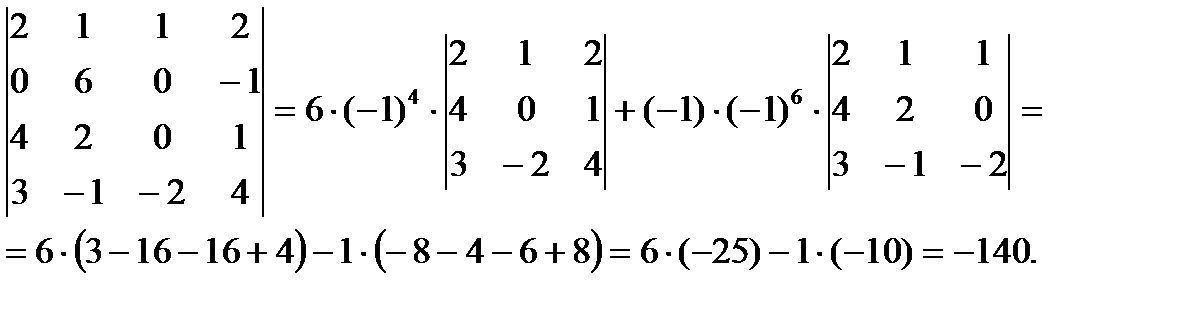
Пример 4.Вычислить определитель четвертого порядка

.

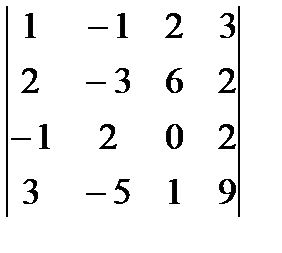Решение. Оставим без изменения первую строку и получим нули в первом столбце. Для этого сложим первую строку с третьей. Затем умножим ее на (-2) и (-3) и сложим соответственно со второй и четвертой строками. Потом разложим определитель по элементам первого столбца.

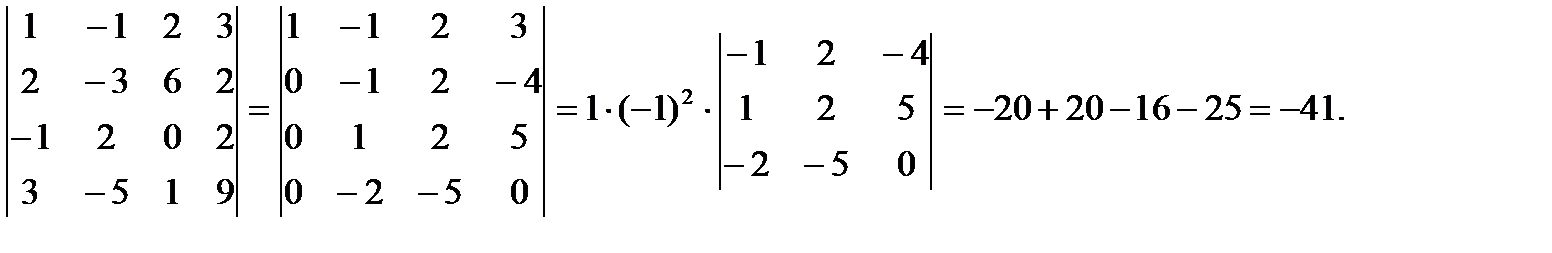
Обратная матрица.

Пусть А – квадратная матрица порядка 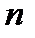, Е - единичная матрица того же порядка :

, .

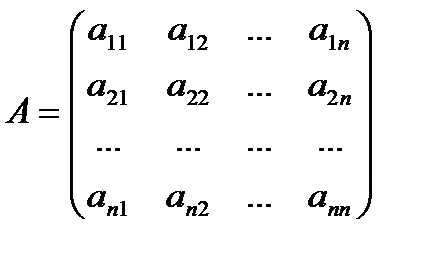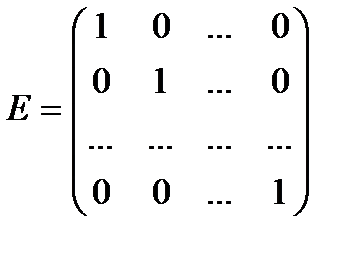Обратной для матрицы А называется матрица, обозначаемая 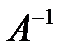и удовлетворяющая равенствам 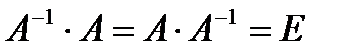. Из определения следует, что обратная матрица может существовать только для квадратной матрицы и обе матрицы имеют один и тот же порядок.

Не всякая квадратная матрица имеет обратную 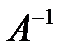. Для ее существования необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля.

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной в противном случае.

Таким образом, обратная матрица существует только для невырожденной матрицы А.

Для невырожденных матриц выполняются следующие свойства:

1.

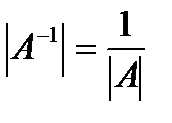
2.

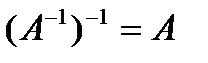
3. .

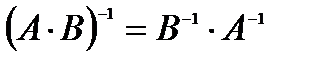Теорема. Матрица ,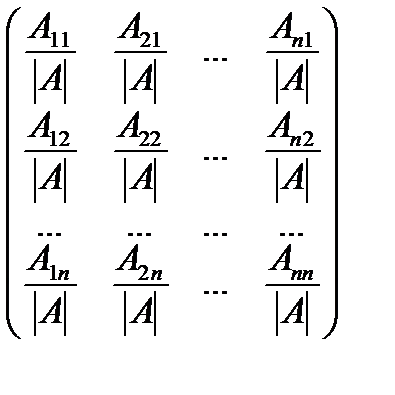

где 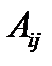- алгебраические дополнения элементов 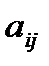невырожденной матрицы А, является обратной для А .