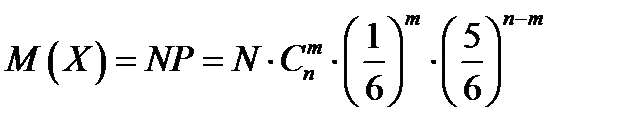Бросают игральных костей. Найти метематическое ожидание числа таких бросаний, в каждом из которых выпадет ровно шестерок, если общее число бросаний равно . 9 страница

Решение:

Из условии задачи следует (поскольку число элементов велико, элементы работают независимо и вероятность отказа каждого элемента мала), что число отказов распределено по закону Пуассона, причём требуется найти параметр 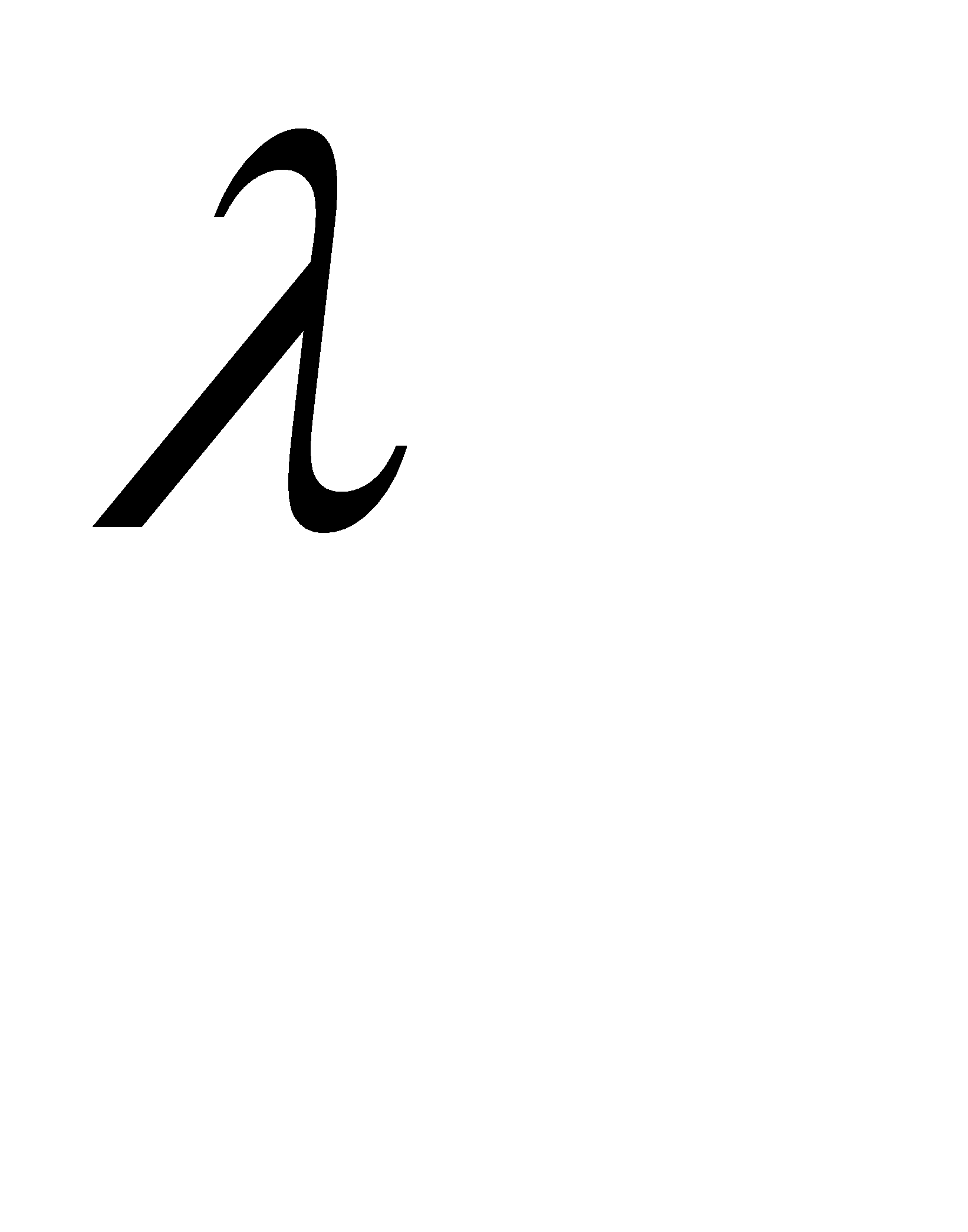(среднее число отказов).

Вероятность того, что откажет хотя бы один элемент, по условию равна 0,98, следовательно .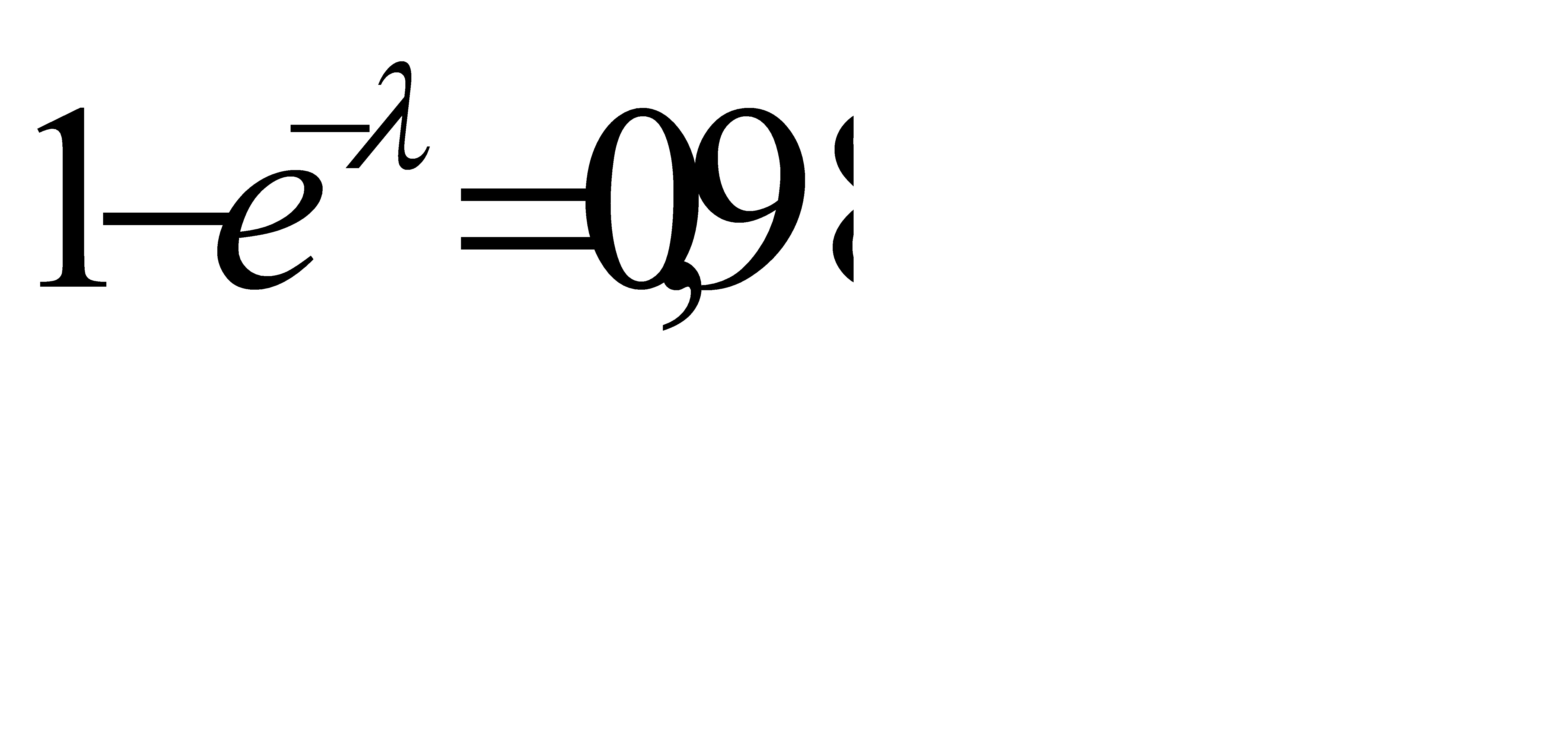

Отсюда

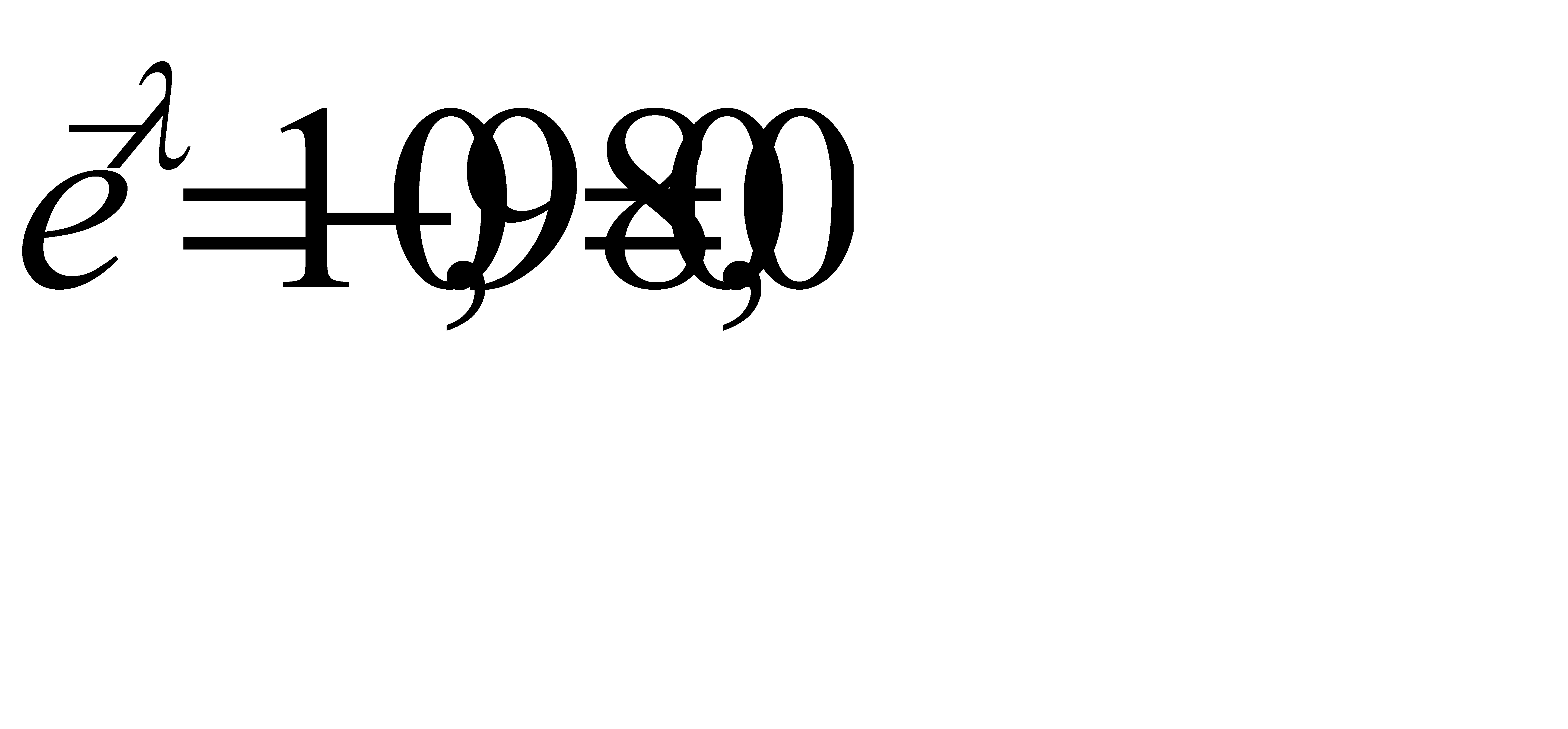
По таблице функции 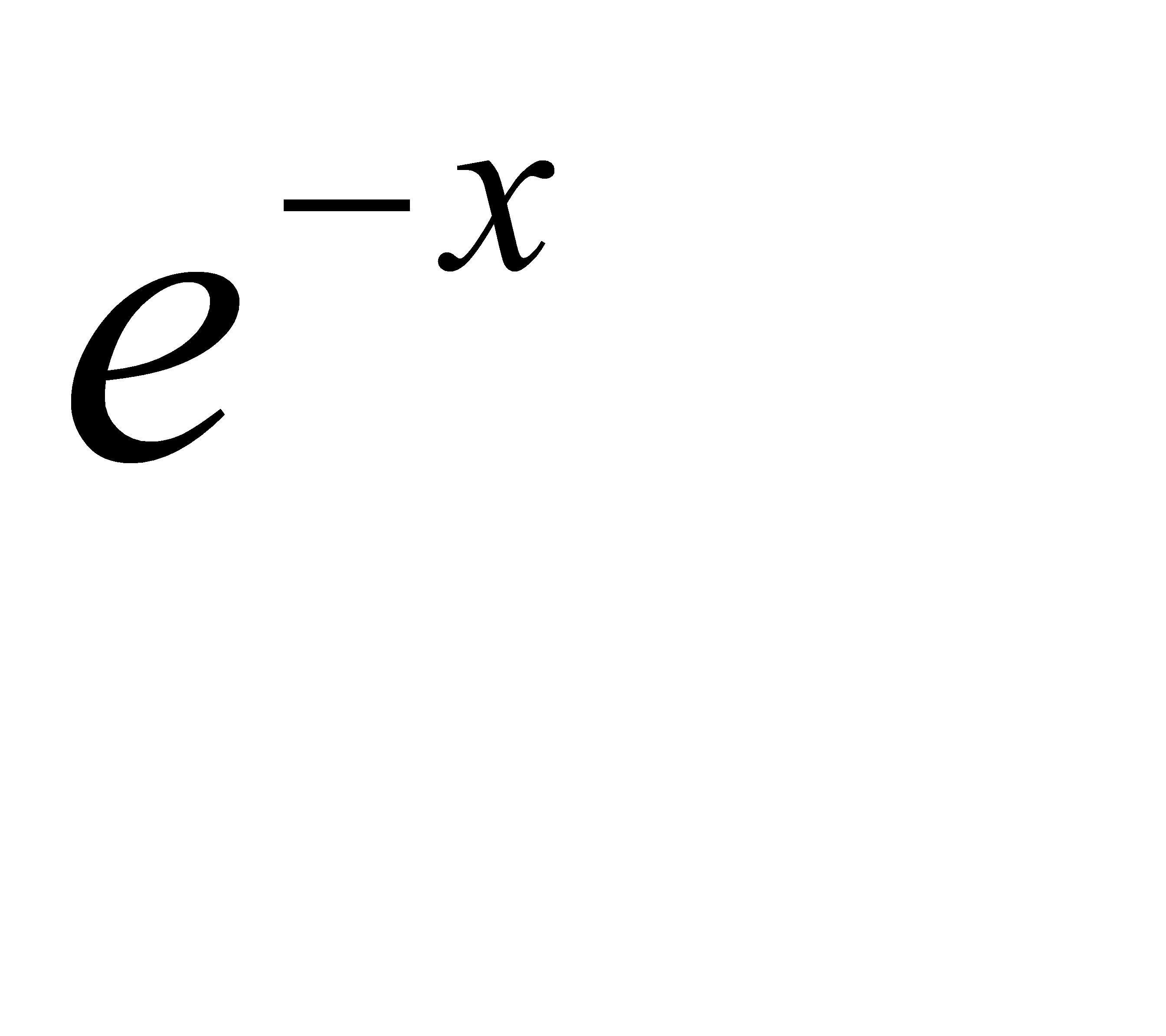находим 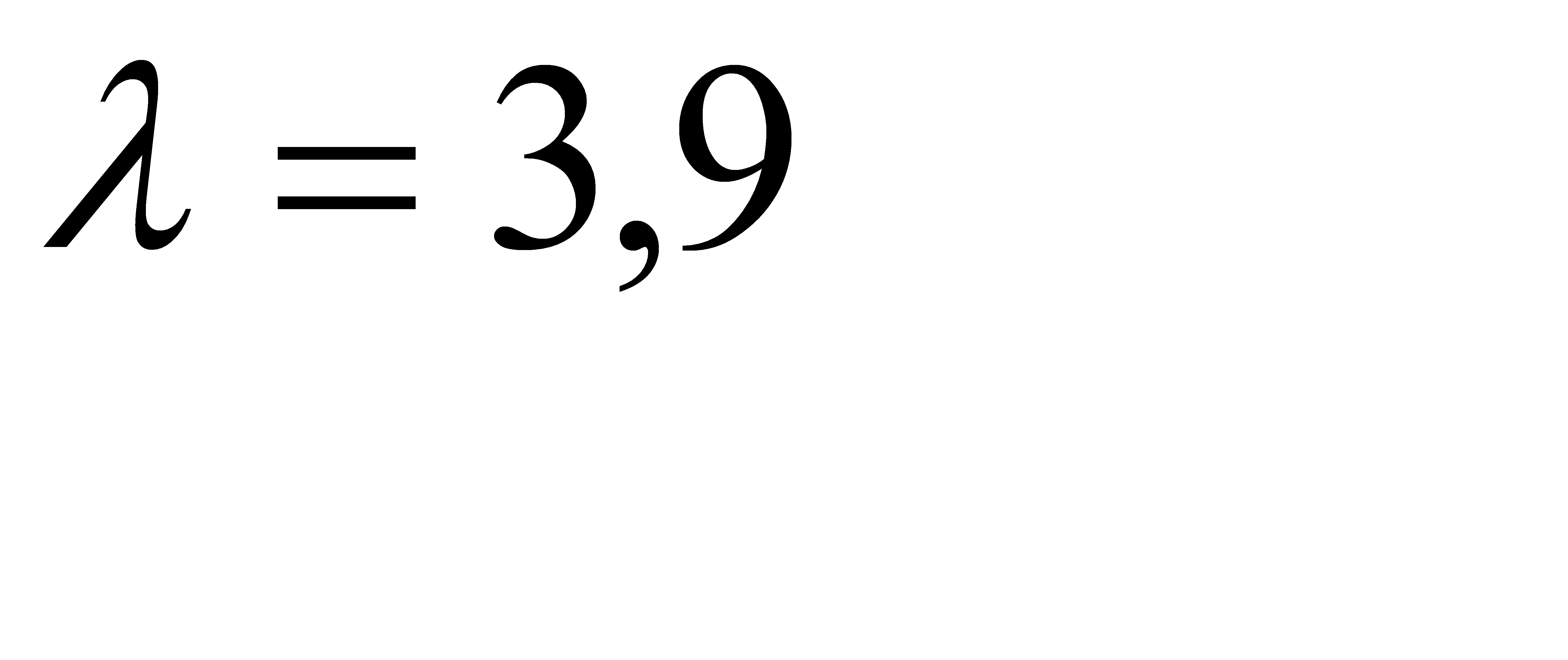. Итак, за время T работы устройства откажет примерно 4 элемента.

Ответ: элемента

б) Найти среднее число бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0,95. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона.

Решение:

Т.к вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0,95, то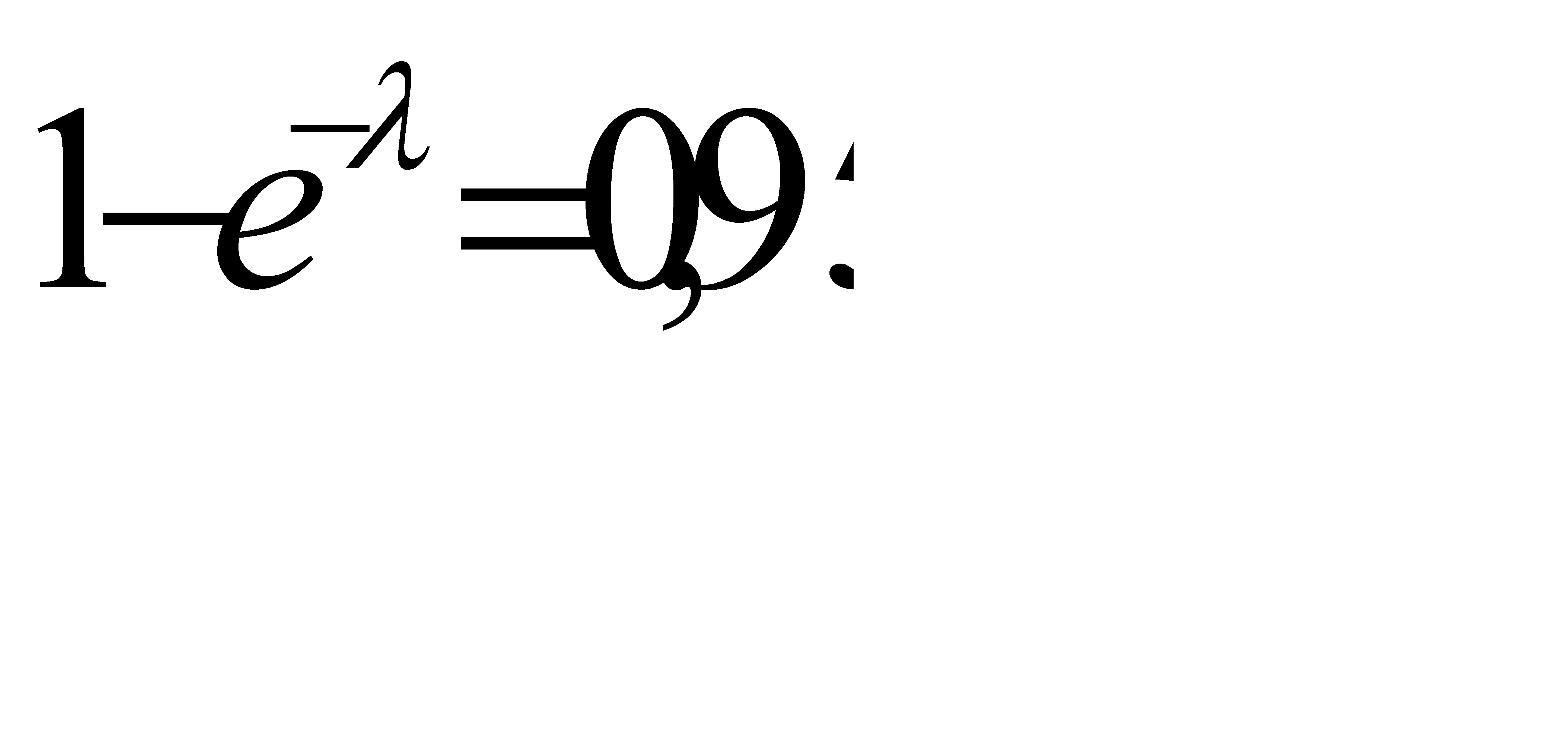

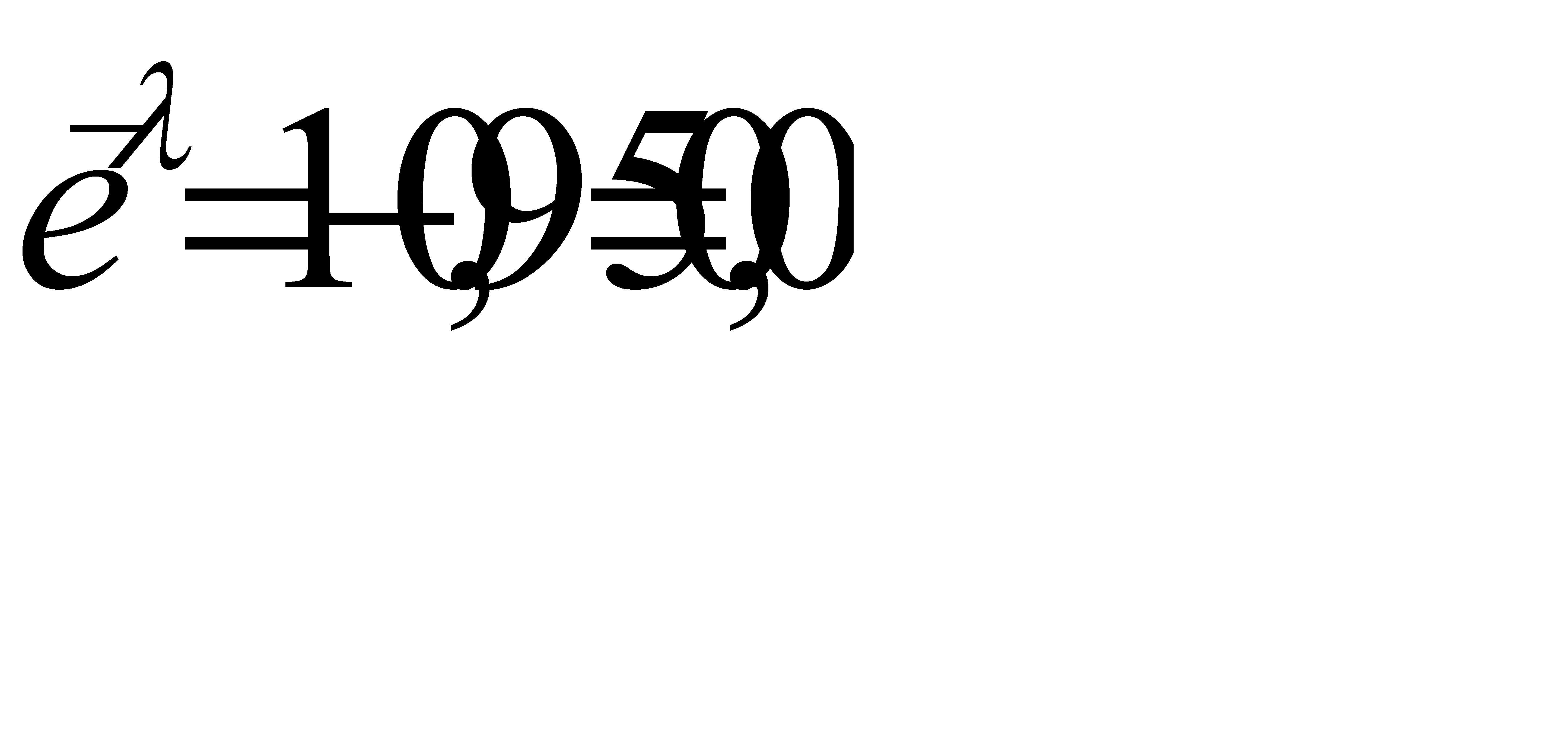
По таблице функции 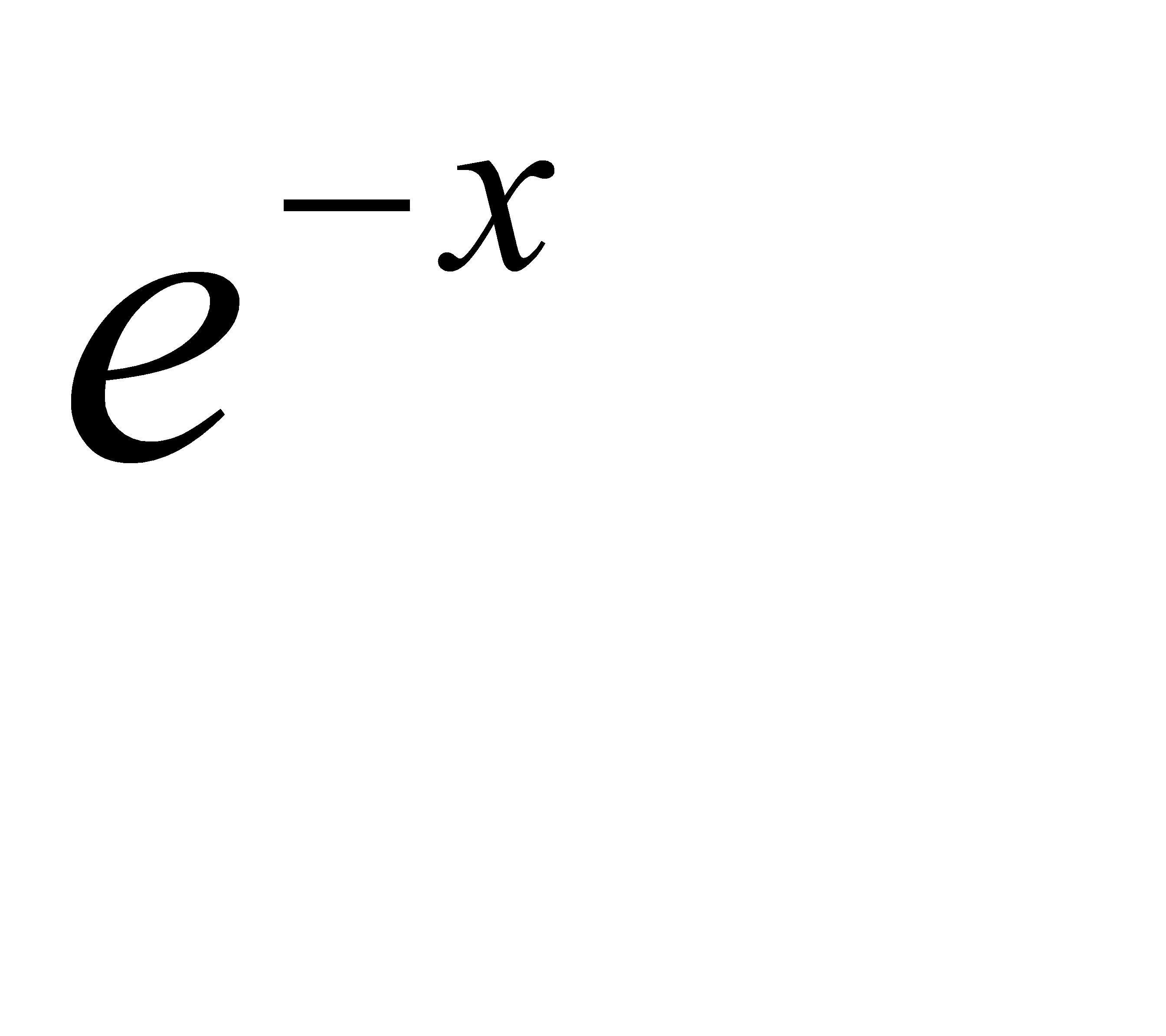находим 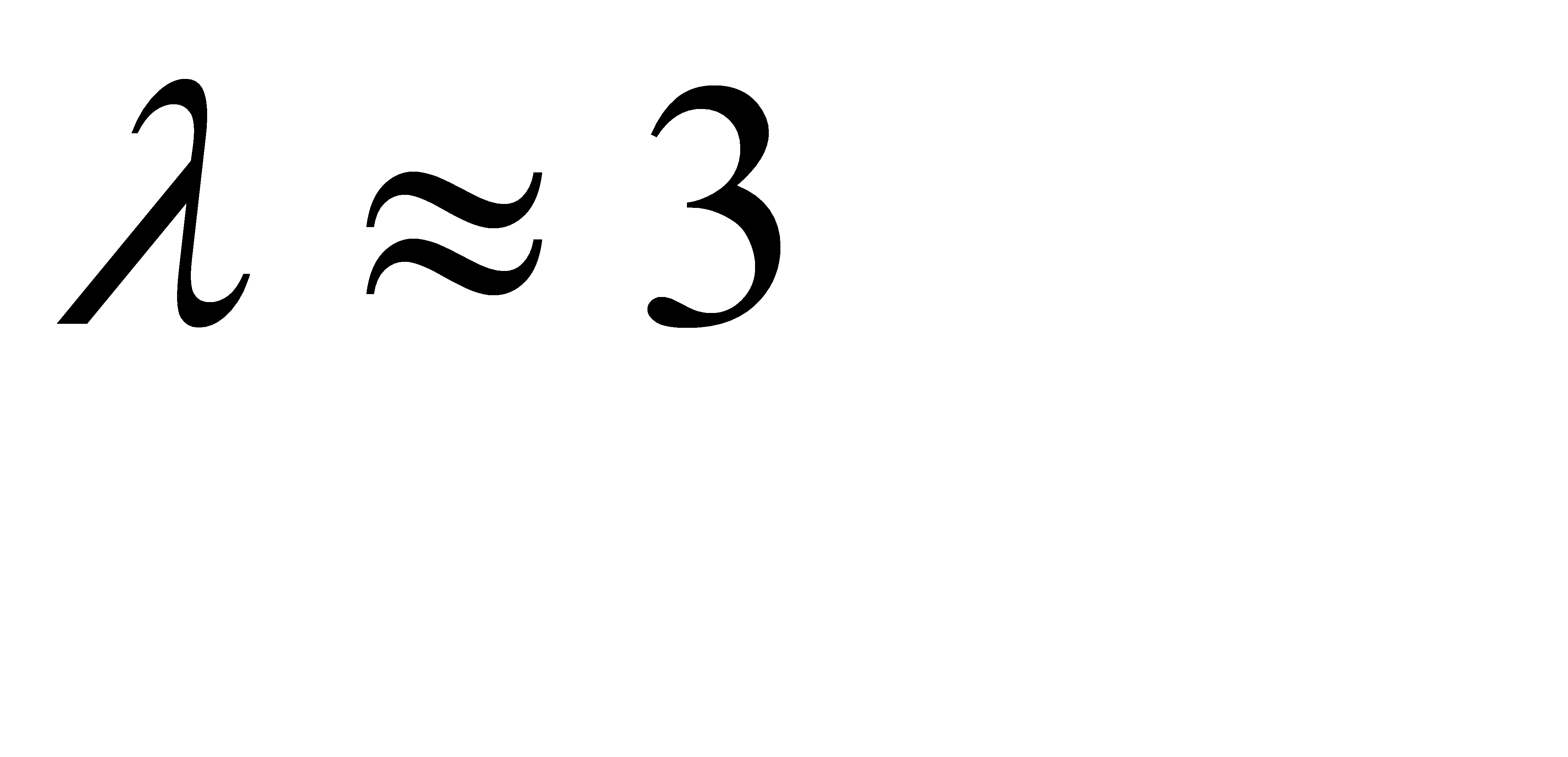. Итак, среднее число бракованных изделий равно 3.

Ответ: 3

№182 Доказать, что сумма вероятностей числа появлений события в независимых испытаниях, вычисленных по закону Пуассона, равна единице. Предполагается, что испытания производятся бесчисленное количество раз.

Решение:

В силу закона Пуассона 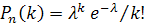используем разложение функции ex в ряд Маклорена:

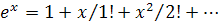
Известно, что этот ряд сходится при любом значении 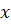, поэтому,

положив 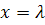, получим

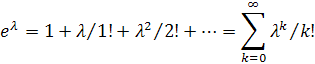
Найдем искомую сумму вероятностей 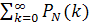, учитывая, что 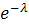не зависит от 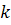и, следовательно, может быть вынесено за знак суммы:

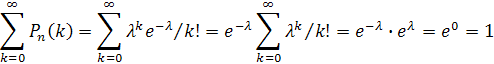
Замечание. Утверждение задачи следует немедленно из того, что сумма вероятностей событий, образующих полную группу, равна единице. Приведенное доказательство преследует учебные цели.

№183 Вероятность выигрыша по одному лотерейному билету .

Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью 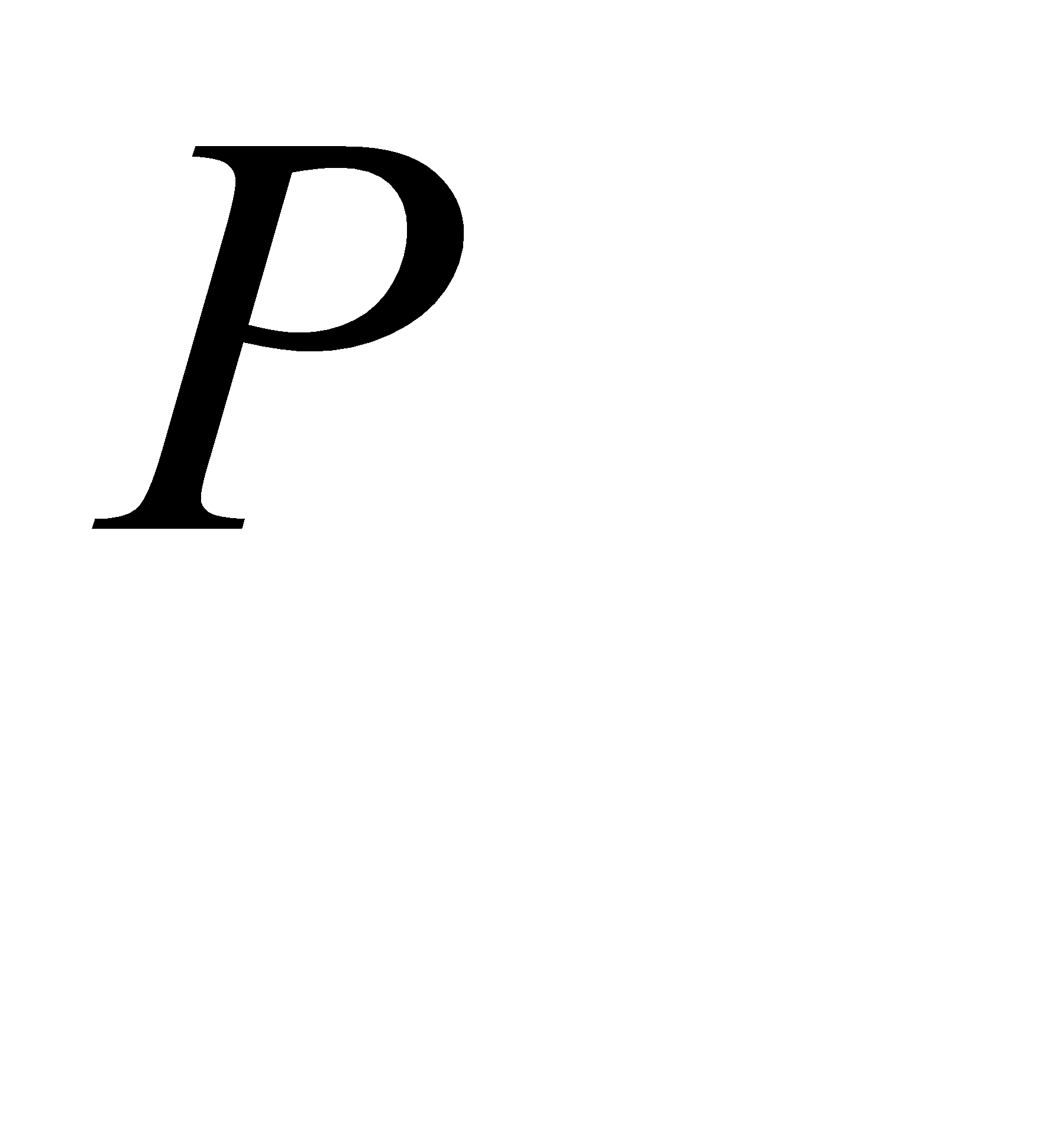, не меньшей, чем ?

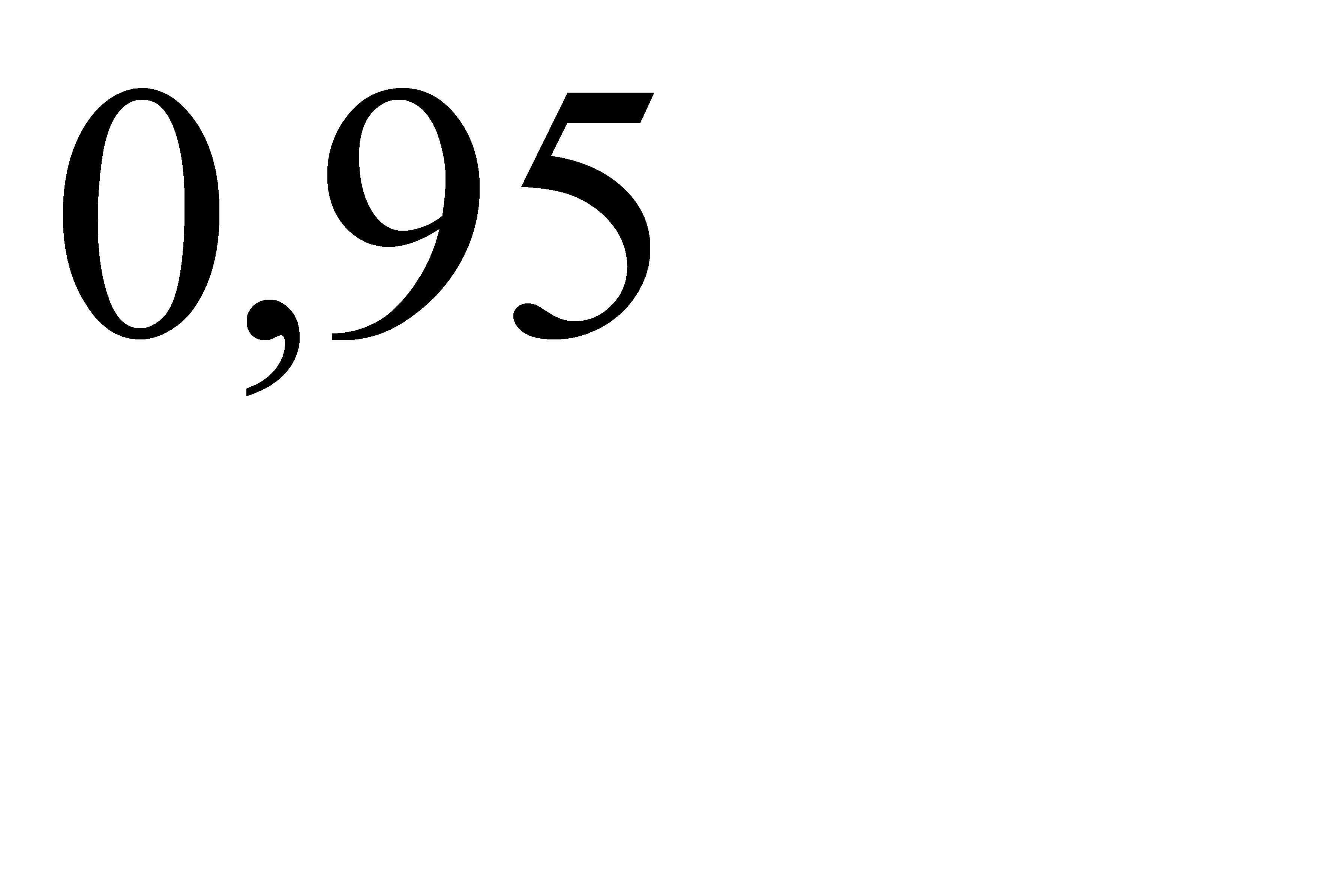Решение:

Вероятность выигрыша мала, а число билетов, которое нужно купить, очевидно, велико, поэтому случайное число выигрышных билетов имеет приближённо распределение Пуассона.

Ясно, что события «ни один из купленных билетов не является выигрышным» и «хотя бы один билет - выигрышный» - противоположные. Поэтому сумма вероятностей этих событий равна единице: Поэтому сумма вероятностей этих событий равна единице:

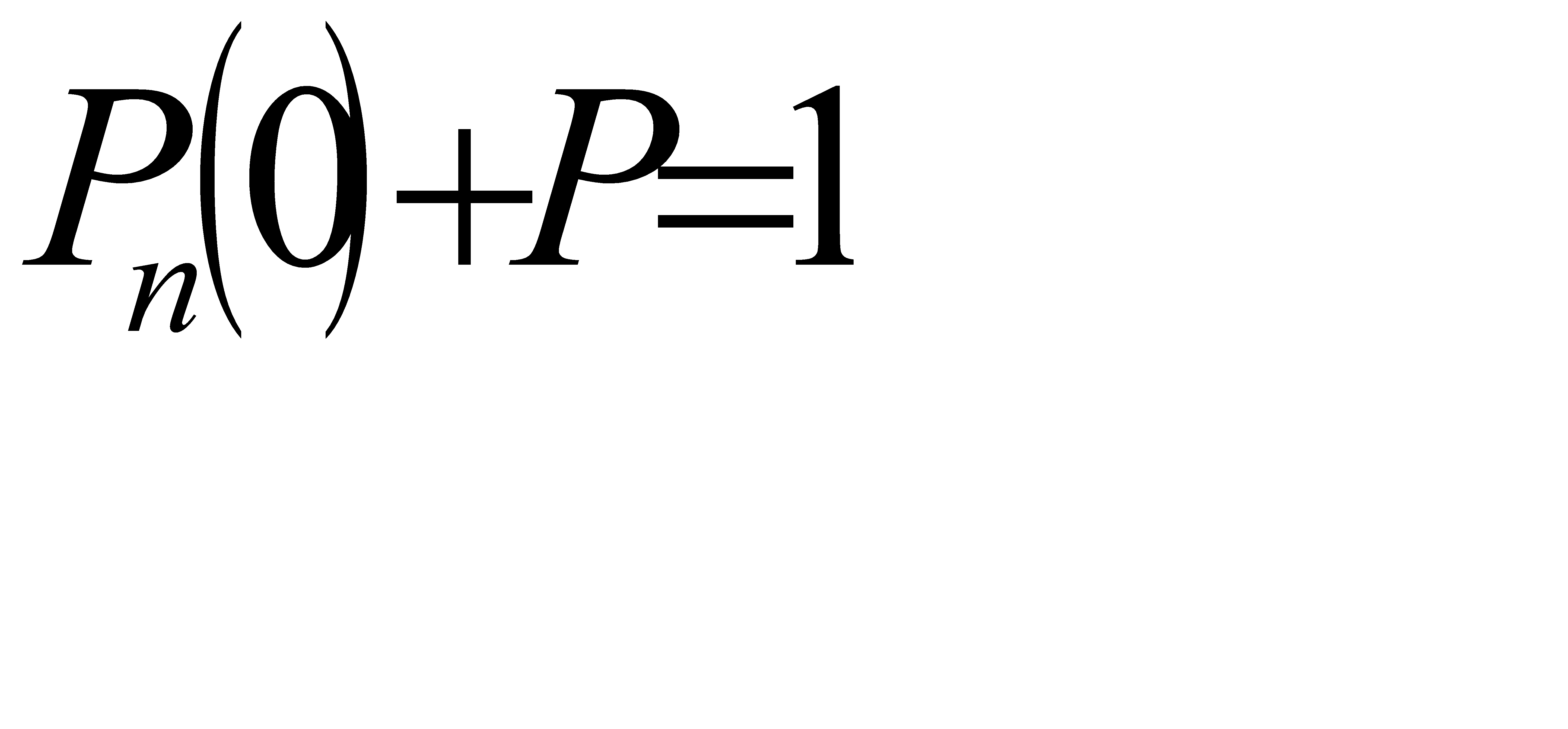, или . (*)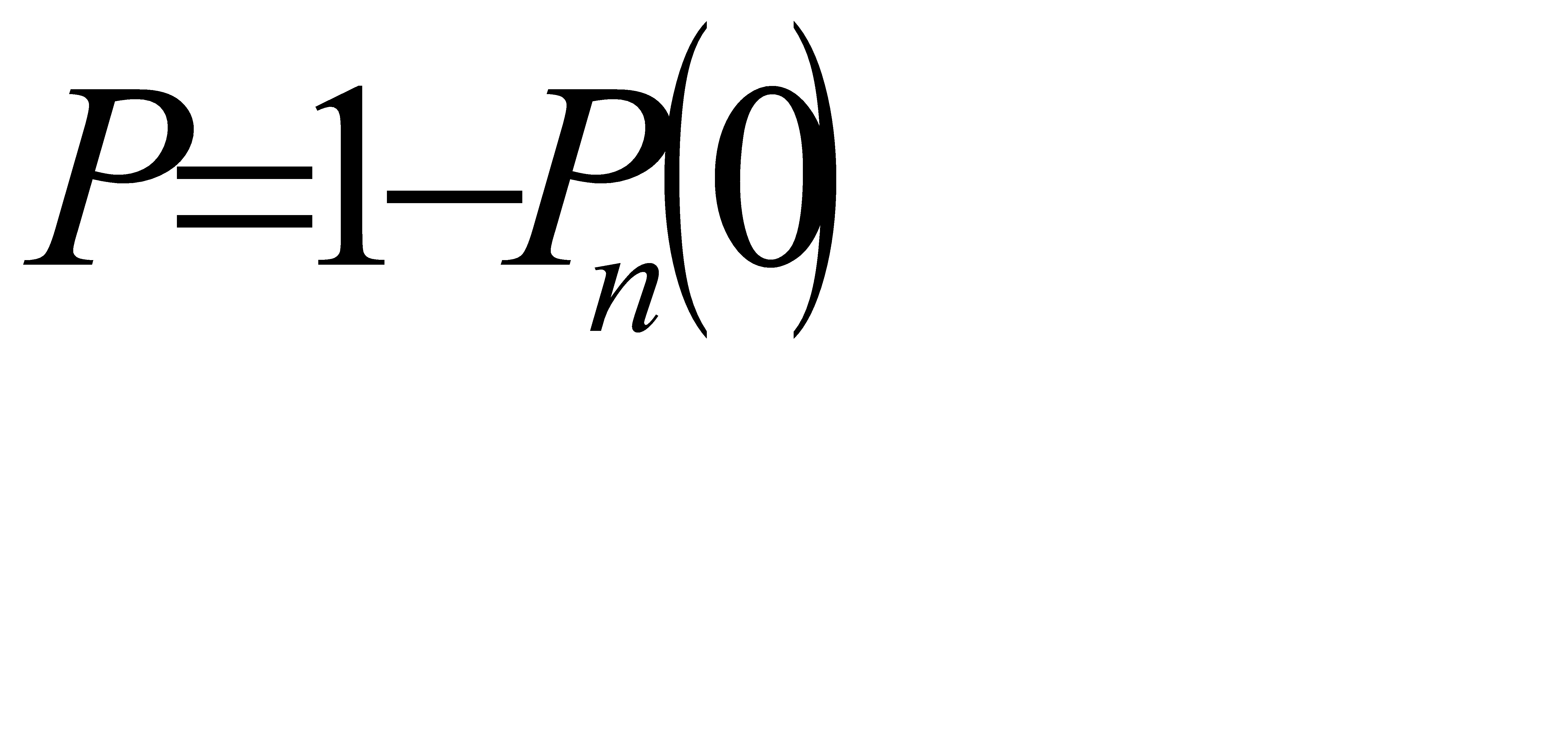

Положив 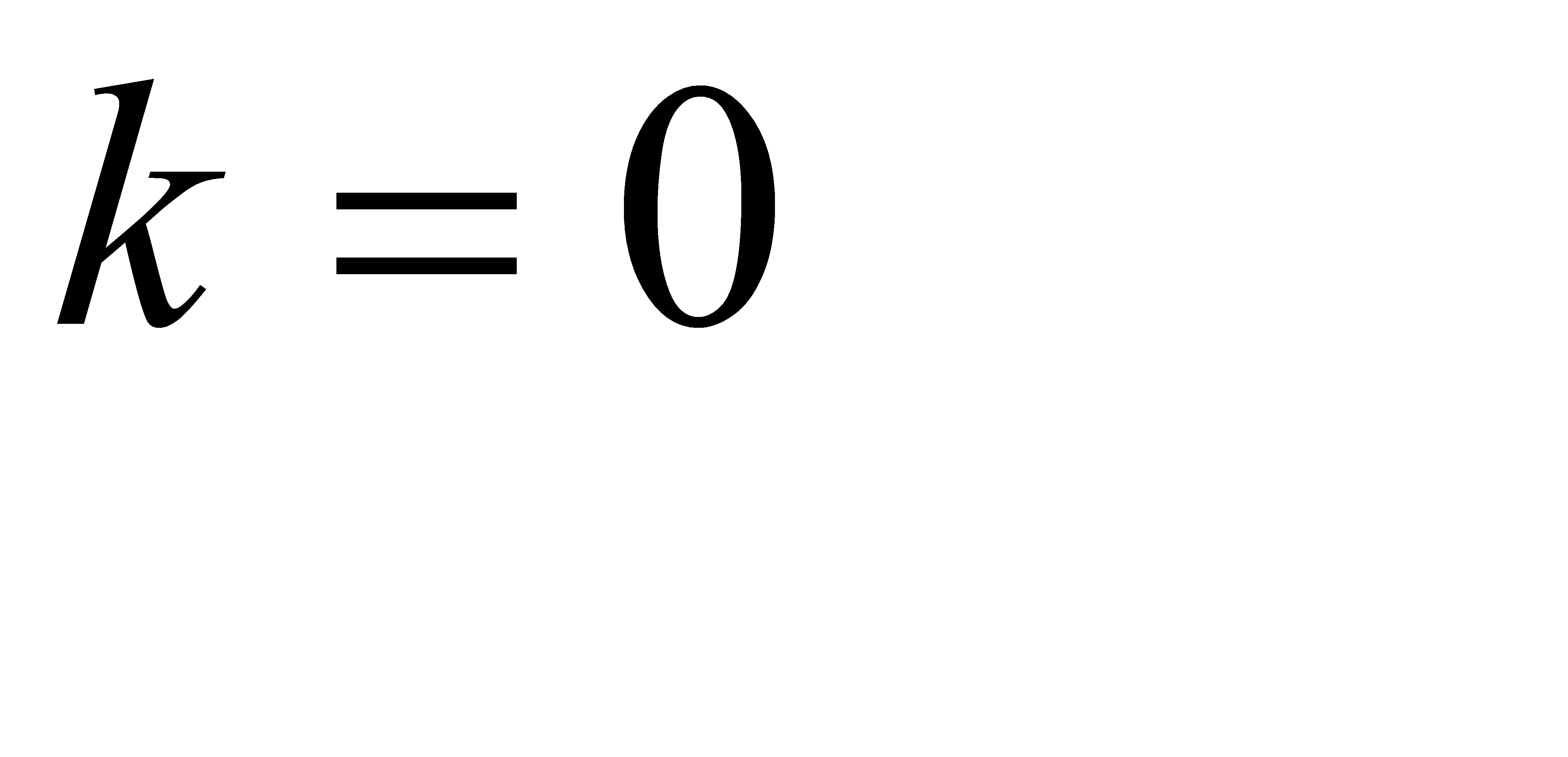в формуле Пуассона 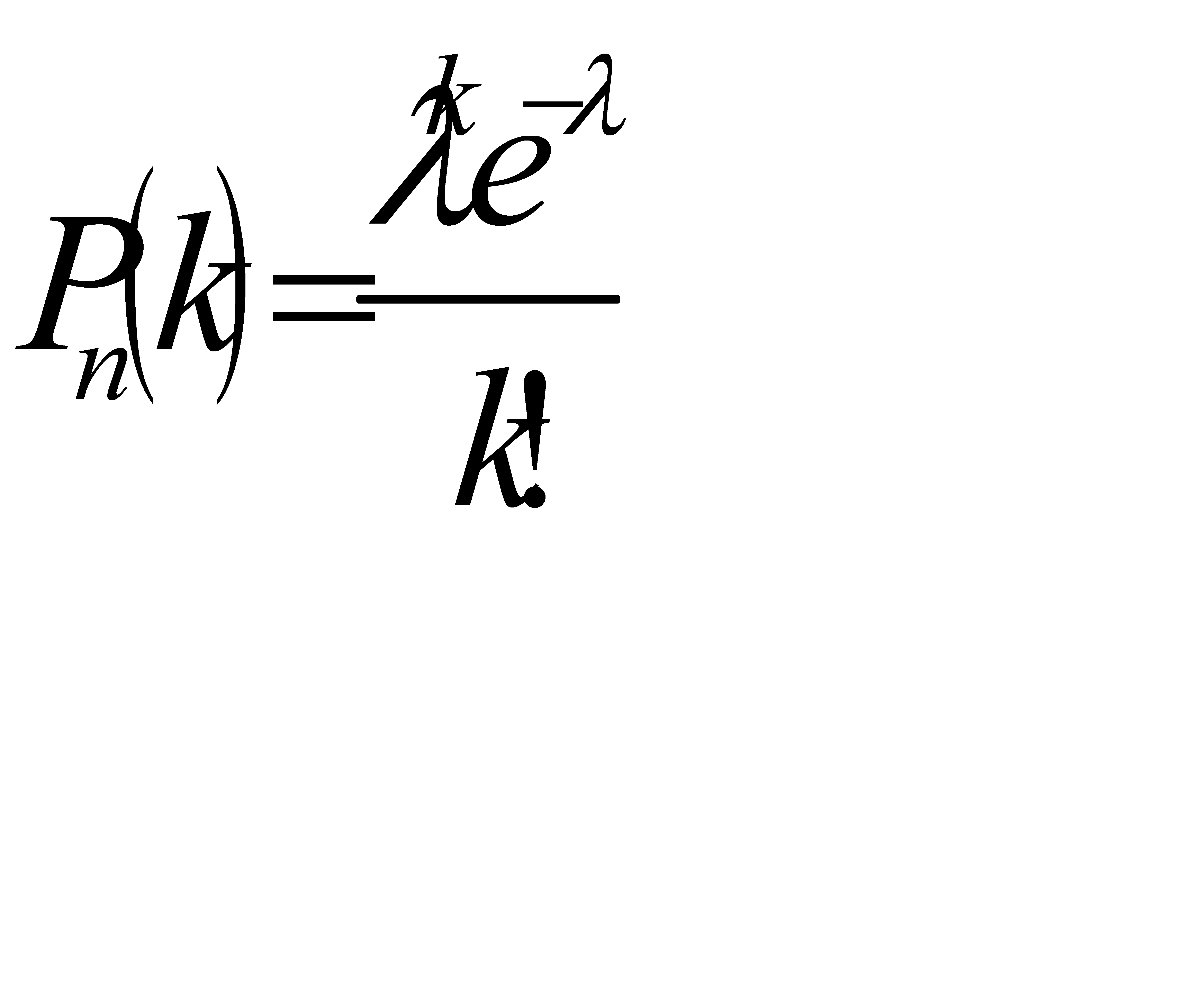, получим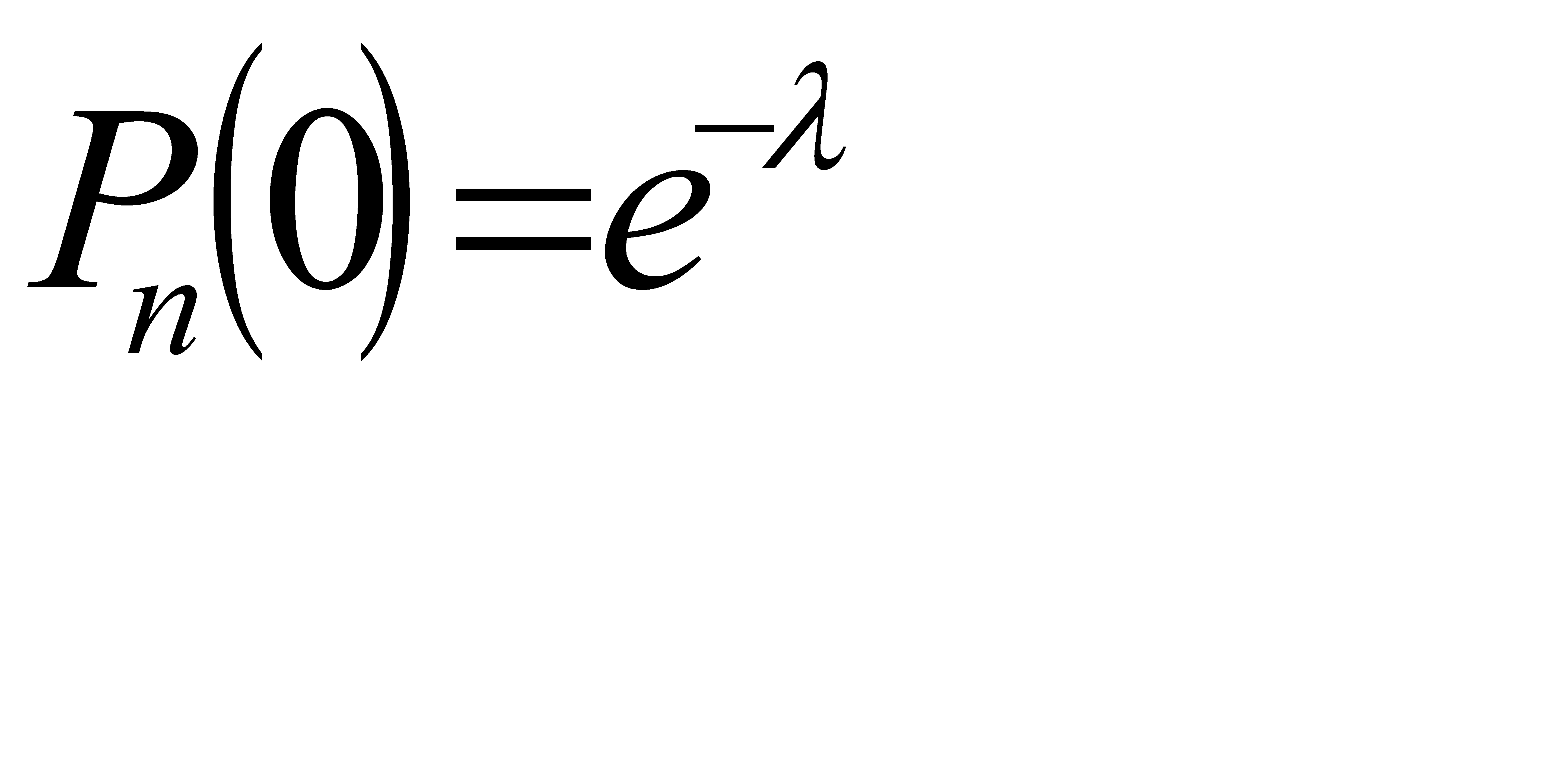

Следовательно, соотношение (*) примет вид .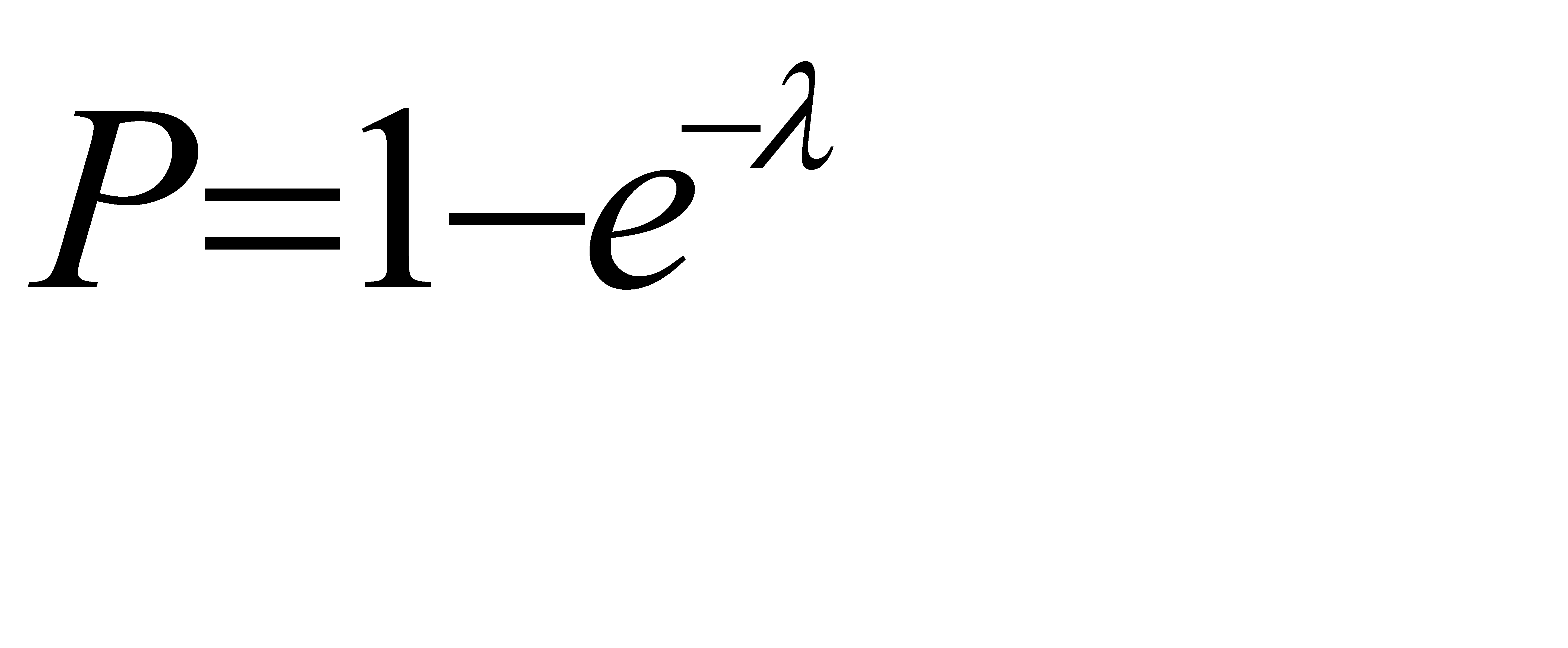

По условию, 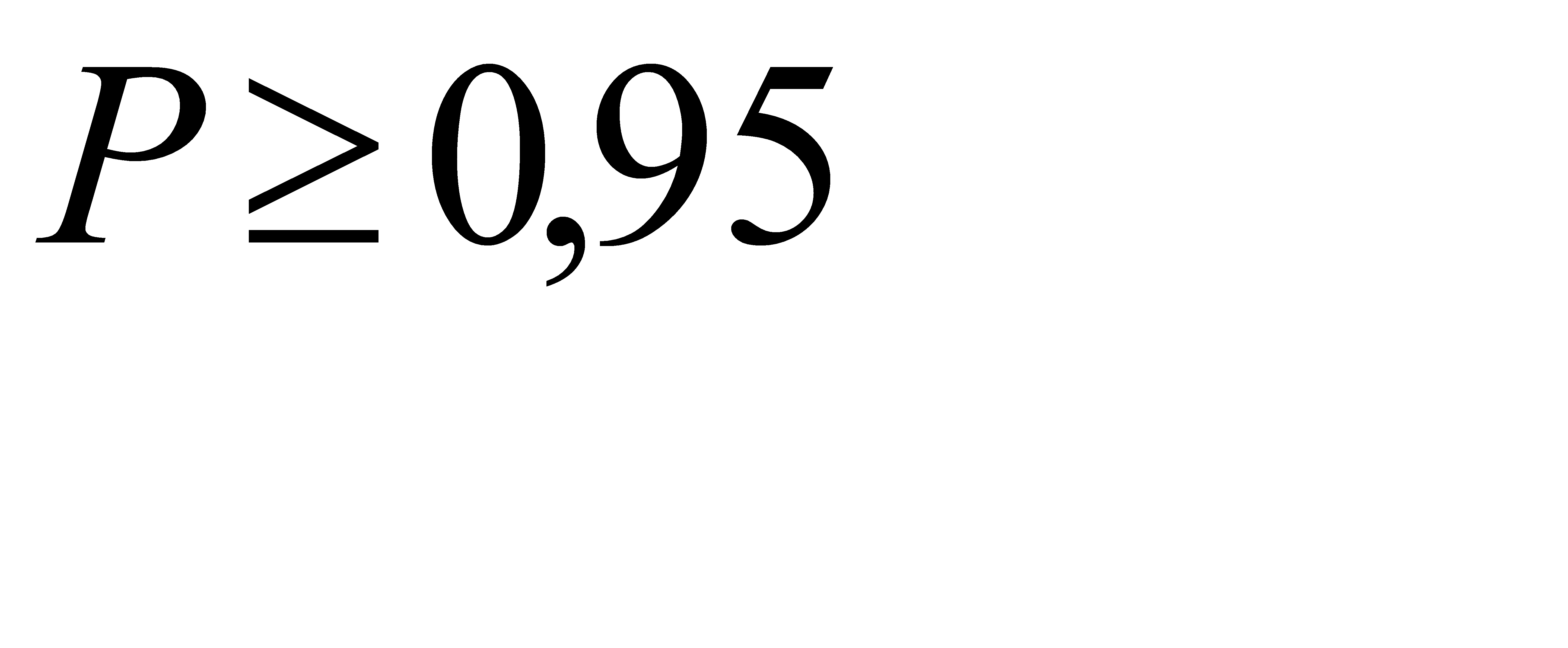, или 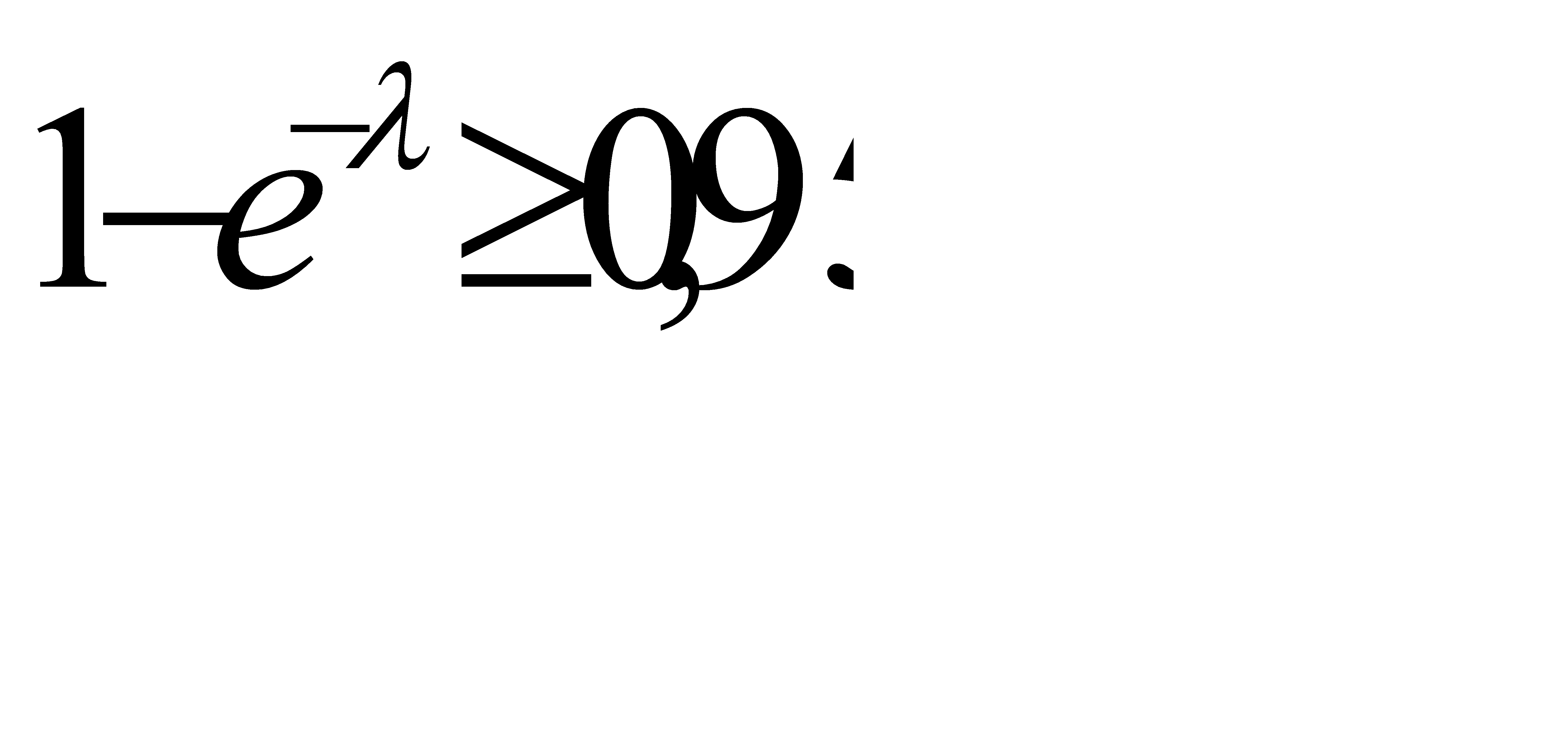. Отсюда . (**)

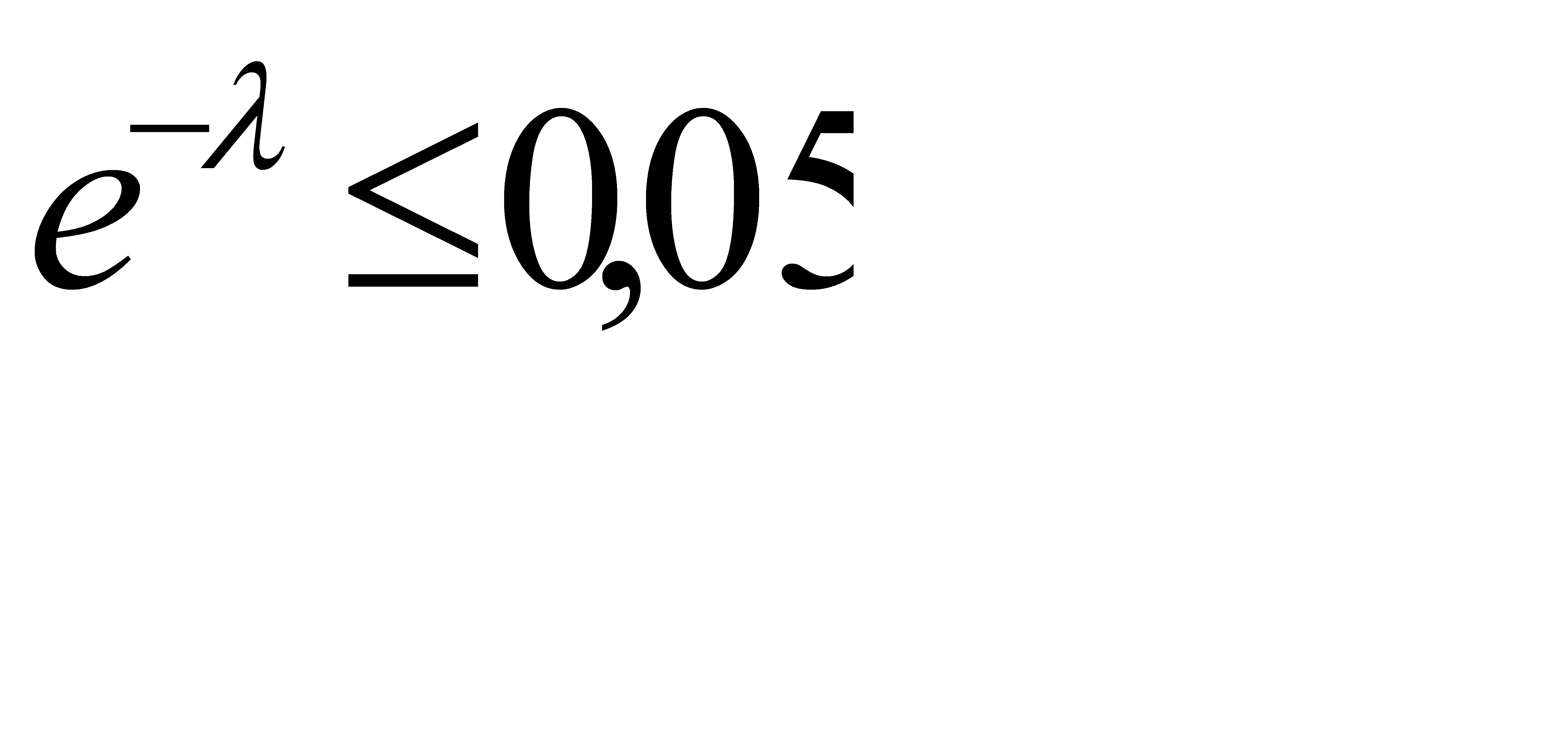По таблице функции 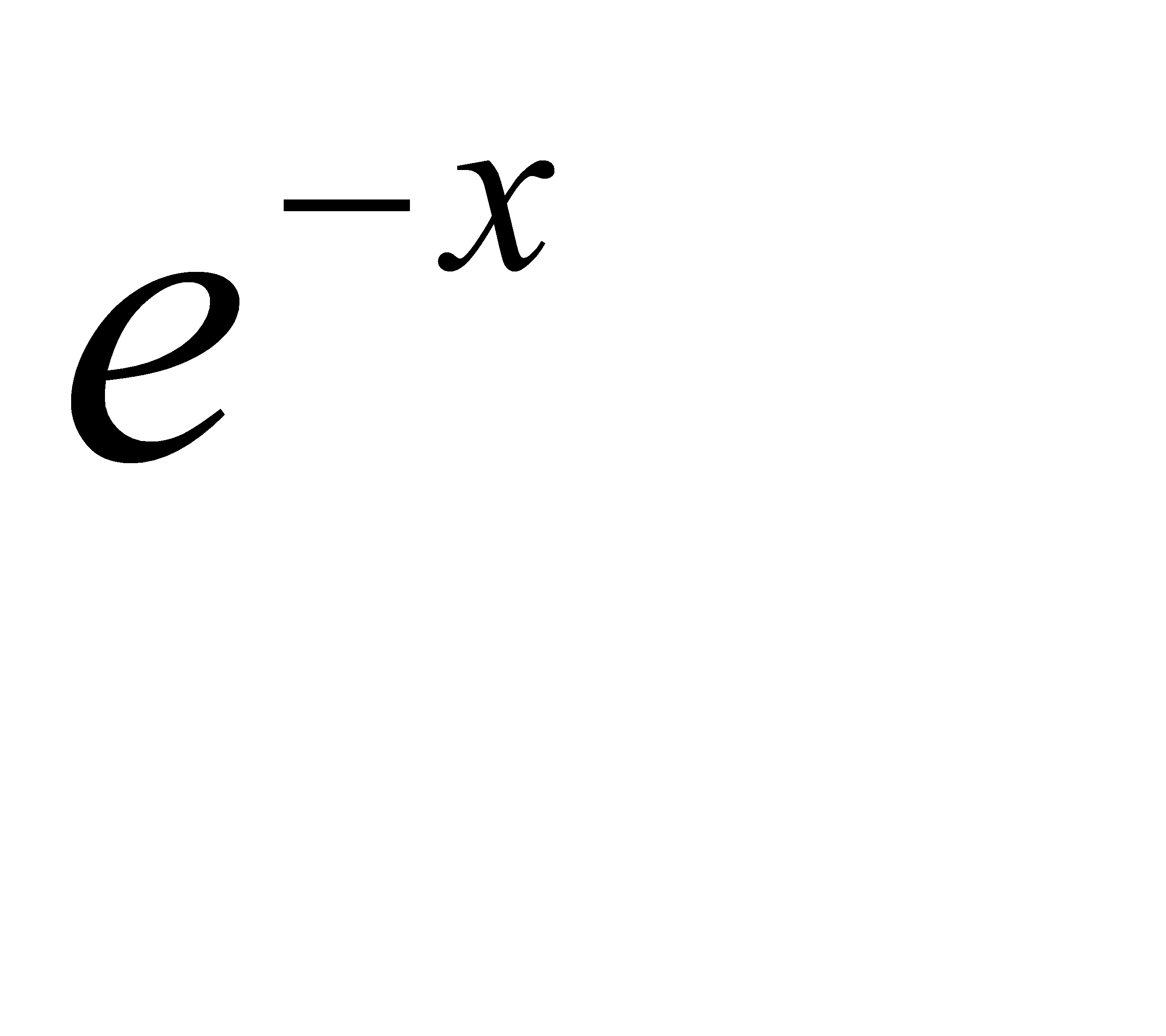находим 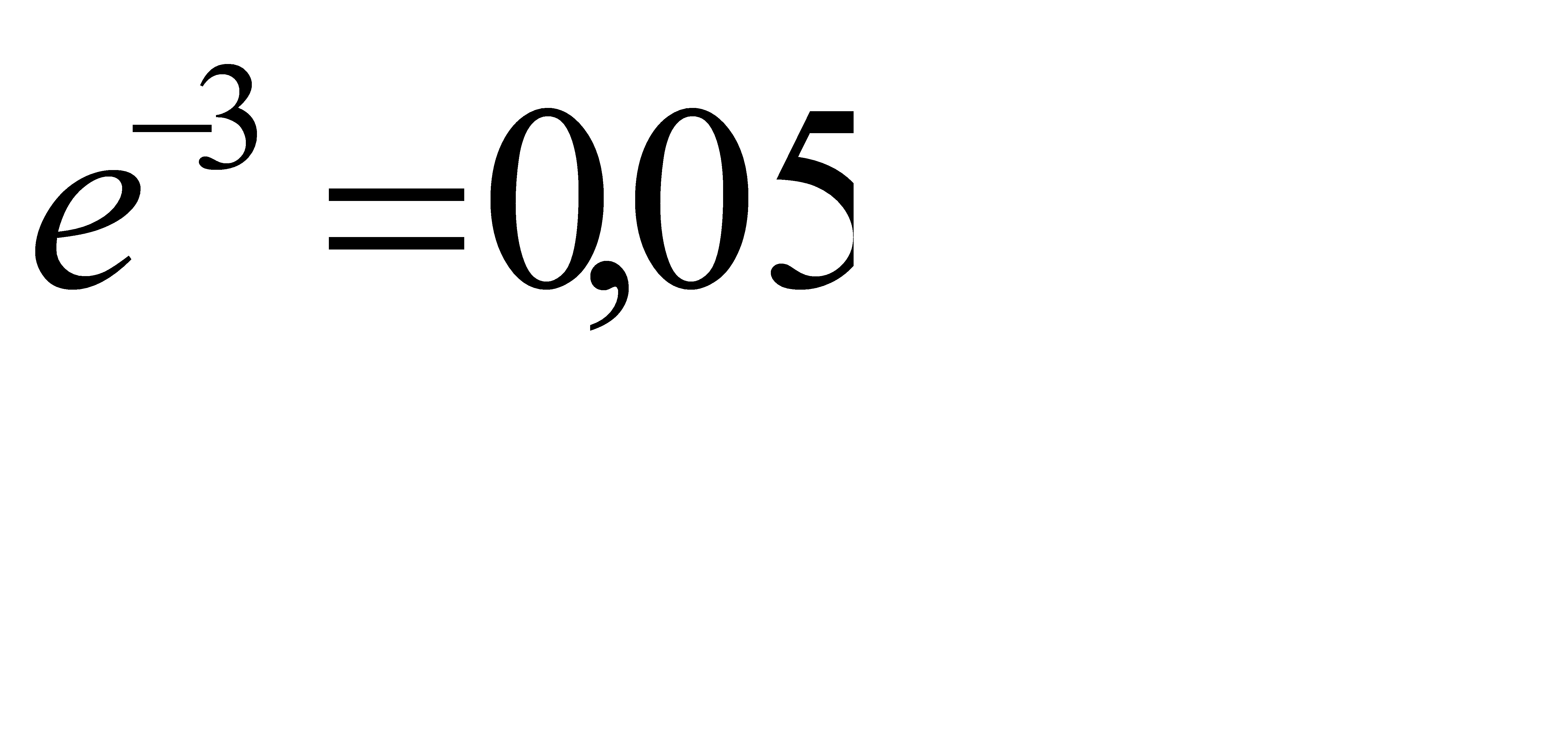. Учитывая, что функция 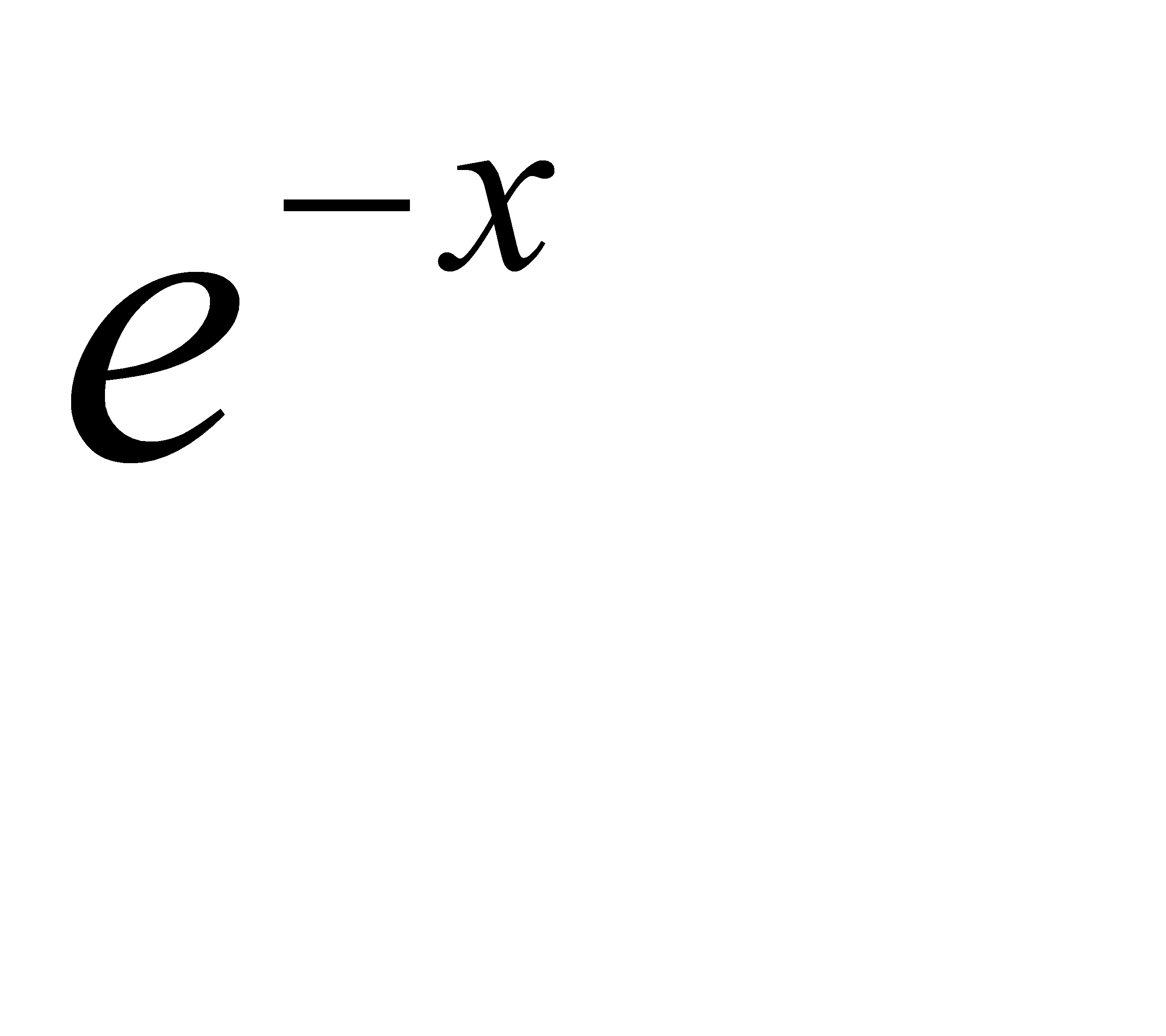- убывающая, заключаем, что неравенство (**) выполняется при 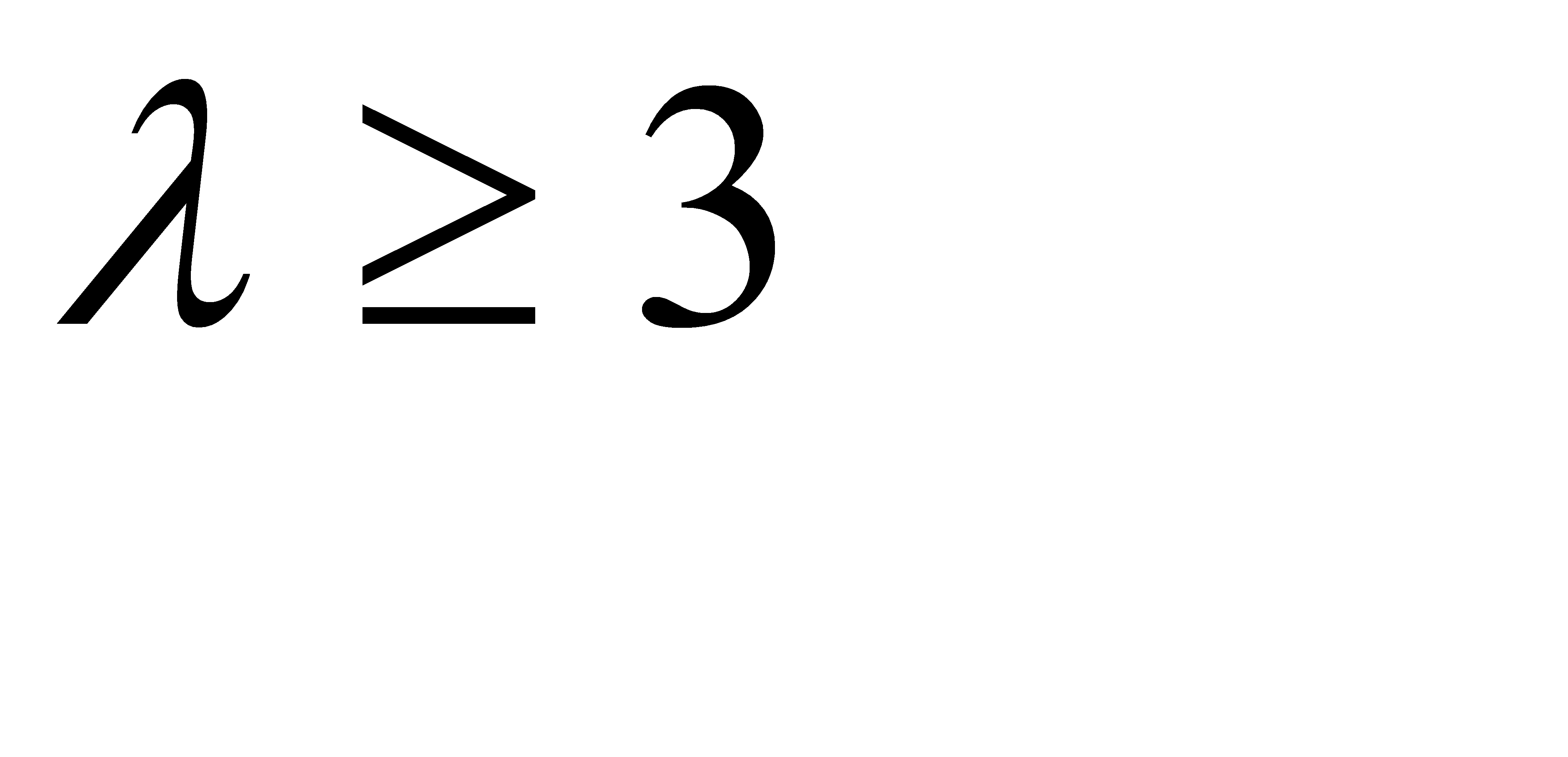, или при 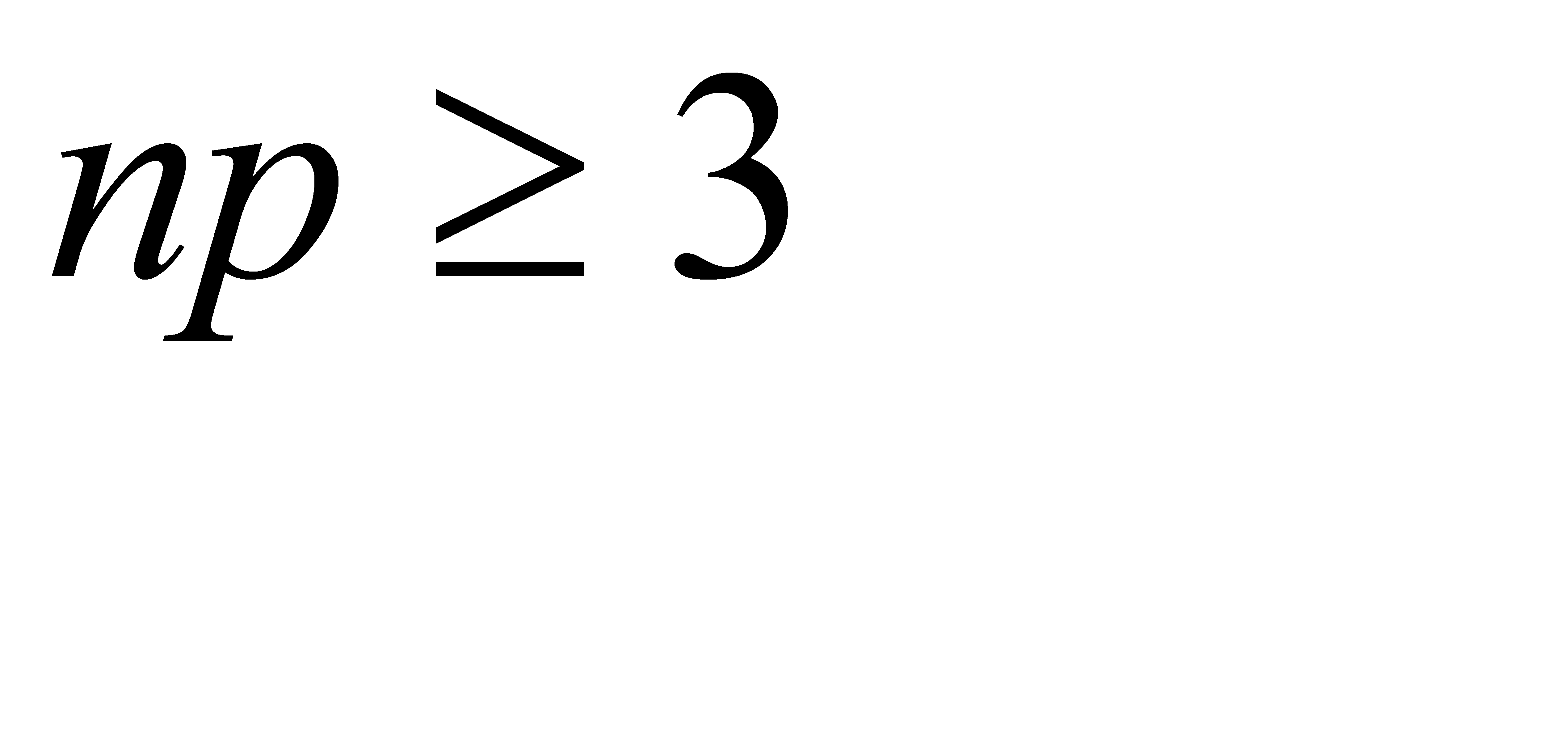. Следовательно, 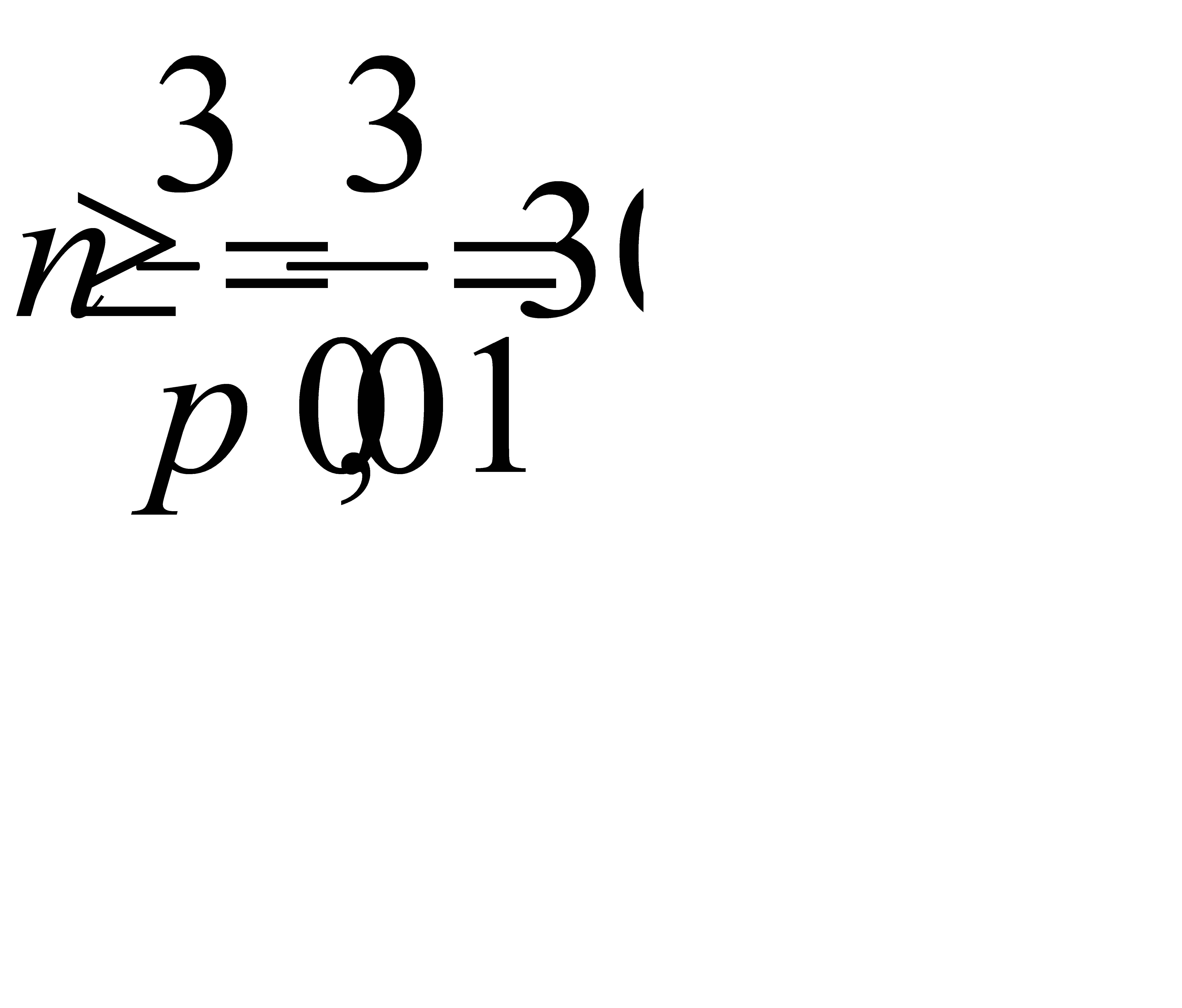. Итак, надо купить не менее 300 билетов, чтобы выиграть хотя бы по одному из них.

№184 Показать, что формулу Пуассона, определяющую вероятность появления k событий за время длительностью t

Pt(k)=( λt)k*e-λt/k! (*)

можно рассматривать как математическую модель простейшего потока событий; другими словами, показать, что формула Пуассона отражает все свойства простейшего потока.

Решение:

Из формулы (*) видно, что вероятность появления k событий за время длительностью t, при заданной интенсивности λ, является функцией только k и t, что отражает свойство стационарности простейшего потока.

Формула (*) не использует информации о появлении событий до начала рассматриваемого промежутка времени, что отражает свойство отсутствия последействия.

Покажем, что формула отражает свойство ординарности. Положив k=0 и k=1, найдем вероятность непоявления событий и вероятность появления одного события:

Pt(0)= e-λt, Pt(1)= λte-λt.

Следовательно, вероятность появления более одного события

Pt(k>1)=1-[ Pt(0)+ Pt(1)]=1-[e-λt+ λte-λt]

Используя разложение функции e-λt в ряд Маклорена, после элементарных преобразований получим

Pt(k>1)=(λt)2/2+… .

Сравнивая Pt (1) и Pt(k>1), получаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что отражает свойство ординарности.

Ч. Т. Д.

№185 Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найти вероятность того, что за 2 мин поступит: а) четыре вызова; б) менее четырех вызовов; в) не менее четырех вызовов.

Решение:

По условию λ=3, t=2,k=4. Воспользуемся формулой Пуассона:

Ptk=λtke-λtk!.

Искомая вероятность того, что за 2 мин поступит 4 вызова:

P24=64e-64!=1296*0,002524=0,135.

б) Событие “поступило менее четырех вызовов” произойдет, если наступит одно из следующих несовместных событий: 1) поступило три вызова; 2) поступило два вызова; 3) поступил один вызов; 4) не поступило ни одного вызова. Эти события несовместны, поэтому применимая теорема сложения вероятностей несовместных событий:

P2k<4=P23+P22+P21+P20=63e-63!+62e-62!+6e-61!+e-6=e-636+18+6+1=0,0025*61=0,1525.

в) События “поступило менее четырех вызовов” и “поступило не менее четырех вызовов” противоположны, поэтому искомая вероятность того, что за 2 мин поступит не менее четырех вызовов:

Pk≥4=1-Pk<4=1-0,1525=0,8475.

№186 Среднее число вызовов, поступающих АТС в одну минуту, равно двум. Найти вероятность того, что за 4 мин поступит: а) три вызова; б) менее трех вызовов; в) не менее трех вызовов. Поток вызовов предполагается простейшим.

Решение:

По условию, λ=2, t=4, k=3

Воспользуемся формулой Пуассона

=

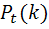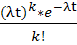
а)вероятность того, что за 4 минуты поступит 3 вызова

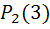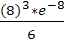= =0.0256

б)Событие “поступило менее 3-х вызовов” произойдет, если поступит одно из несовместных событий: поступило 2 вызова или поступил 1 вызов или вызовов не поступило

Эти события несовместны, поэтому применима теорема сложения вероятностей несовместных событий:

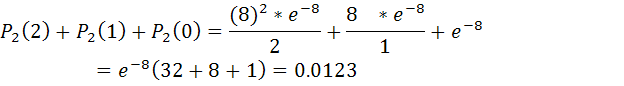
в)События “поступило менее 3-х вызовов” и “поступило не менее 3-х вызовов” противоположны, поэтому искомая вероятность того, что за 4 минуты поступит не менее 3-х вызовов:

P(k≥3)=1-P(k<3)=1-0.0123=0.9877

№187 Доказать, что для простейшего потока событий

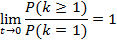
Решение:

Воспользуемся теоремой о сумме вероятностей противоположных событий: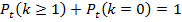

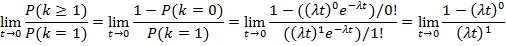
Применяя правило Лопиталя получим

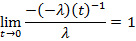
Ч.Т.Д.

№188 Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:

X	-4
p	0,2	0,3	0,5

а)

X	0,21	0,54	0,61
P	0,1	0,5	0,4

б)

Решение:

а) Математическое ожидание равно сумме произведений всех возможных значений 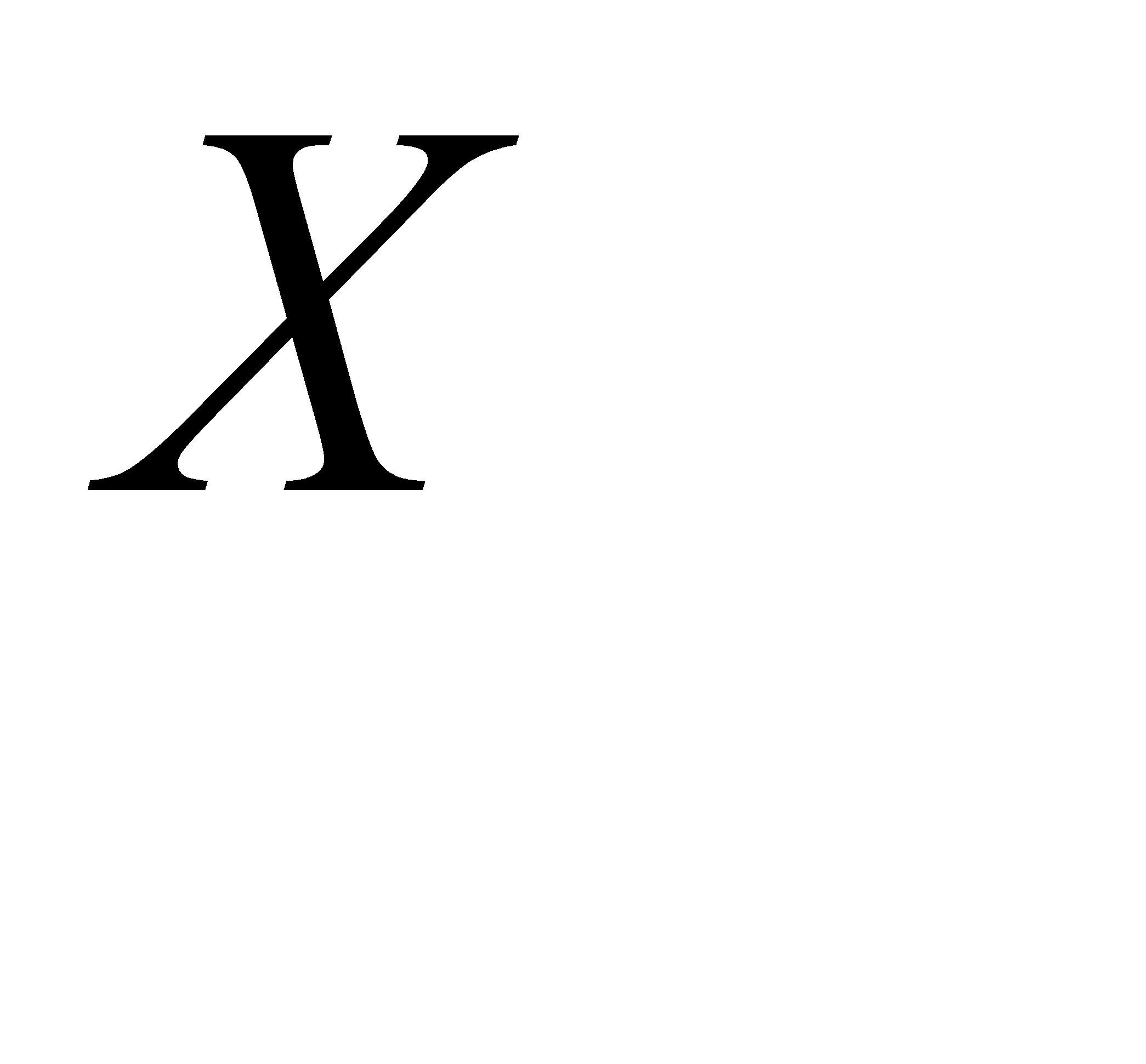на их вероятности:

.

б) .

№189 Найти математическое ожидание случайной вели-

величины Z, если известны математические ожидания X и Y:

a) Z = X + 2Y, Af(X) = 5, M(Y) = 3; б) Z = 3X+4Y,

Af(X) = 2, M(Y) = 6.

Решение:

а) Используя свойства математического ожидания

(математическое ожидание суммы равно сумме математических ожи-

ожиданий слагаемых; постоянный множитель можно вынести за знак

математического ожидания), получим

М (Z) = М (X + 2К) = М (X) + М (Y) = М (X)+2М (К) =

=5+2-3=11.

б) Аналогично пункту а) получим:

M(Z)=M(3X+4Y)=3M(X)+4M(Y)=3*2+4*6=30

№190 Используя свойства математического ожидания, доказать, что: а) 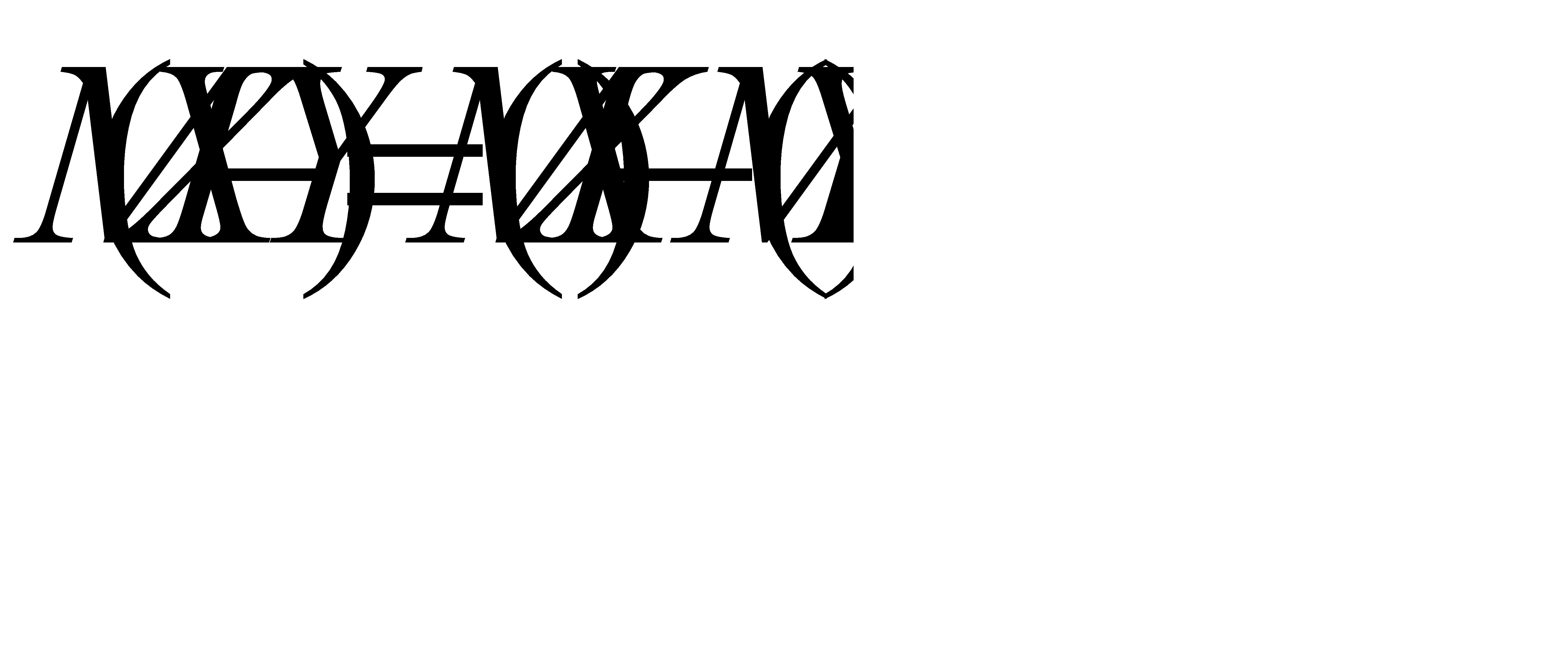, б) математическое ожидание отклонения 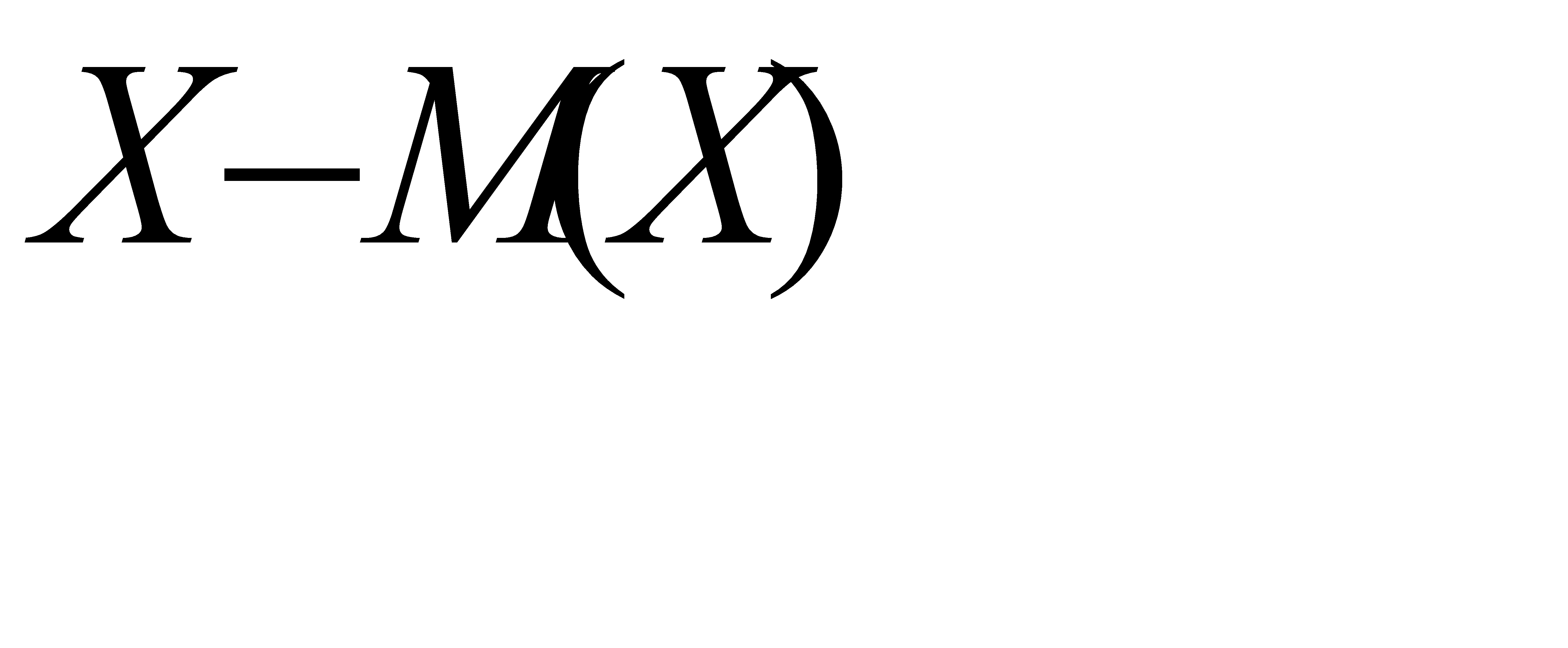равно нулю.

Решение:

а) Положим 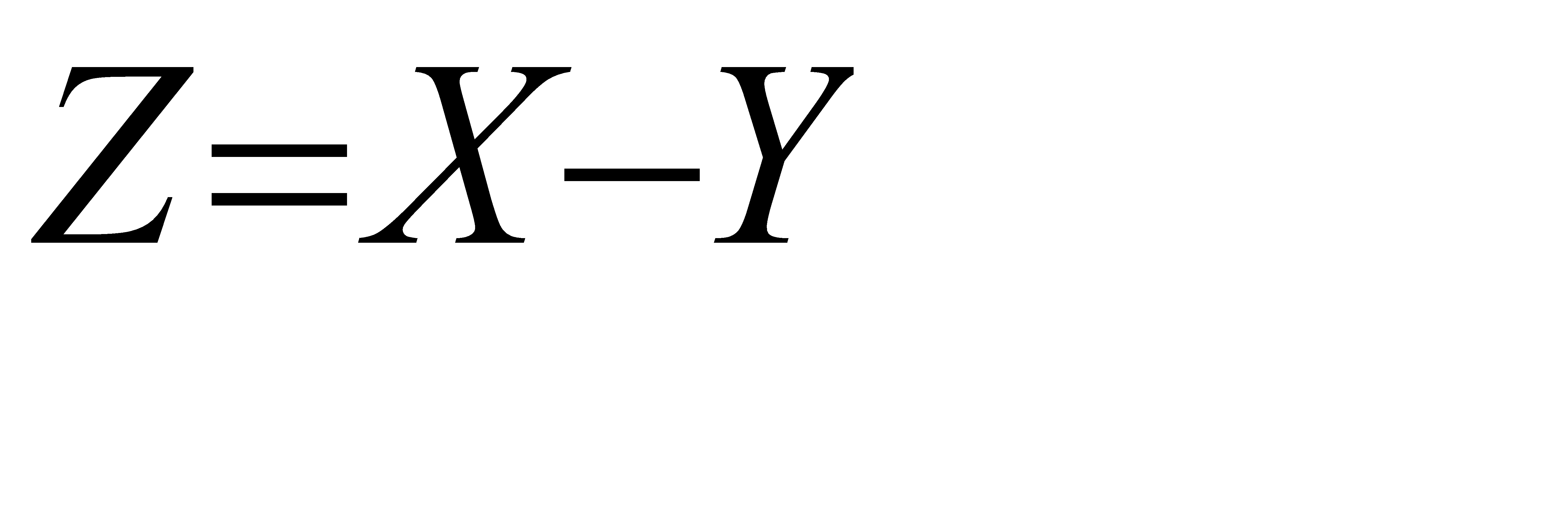. Тогда 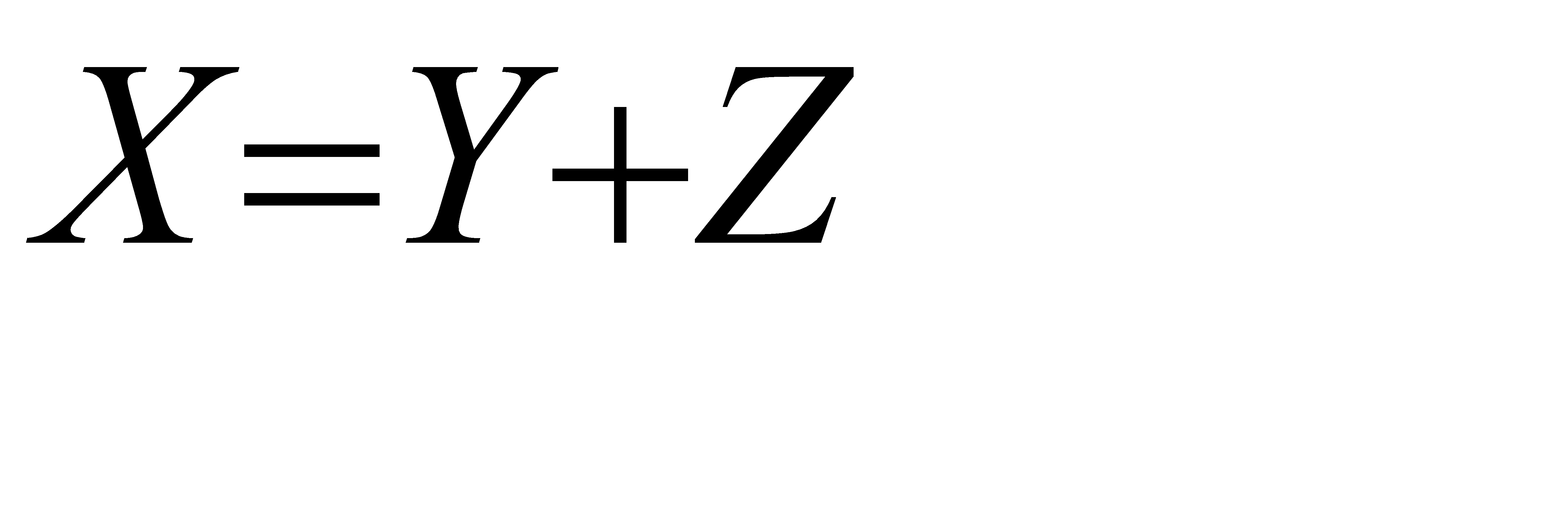. Из свойства 4 математического ожидания следует, что 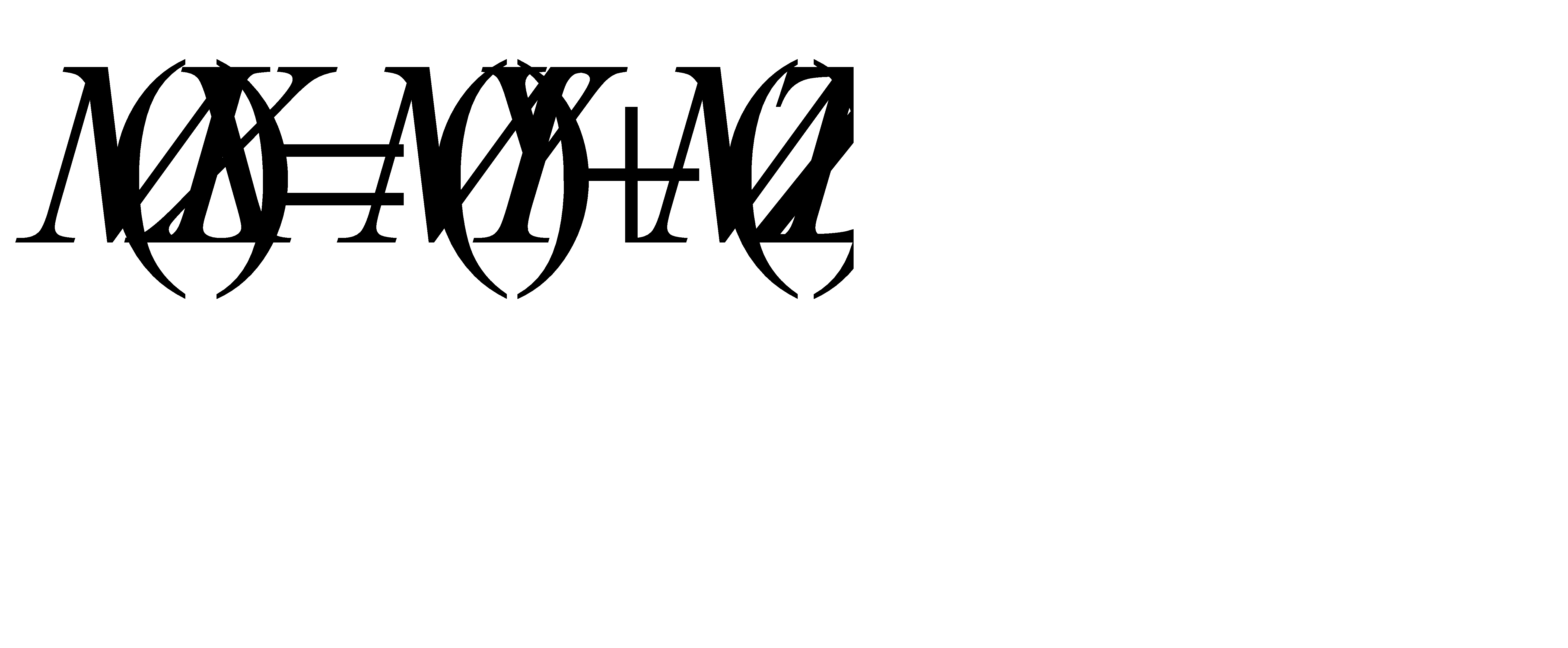. Отсюда .

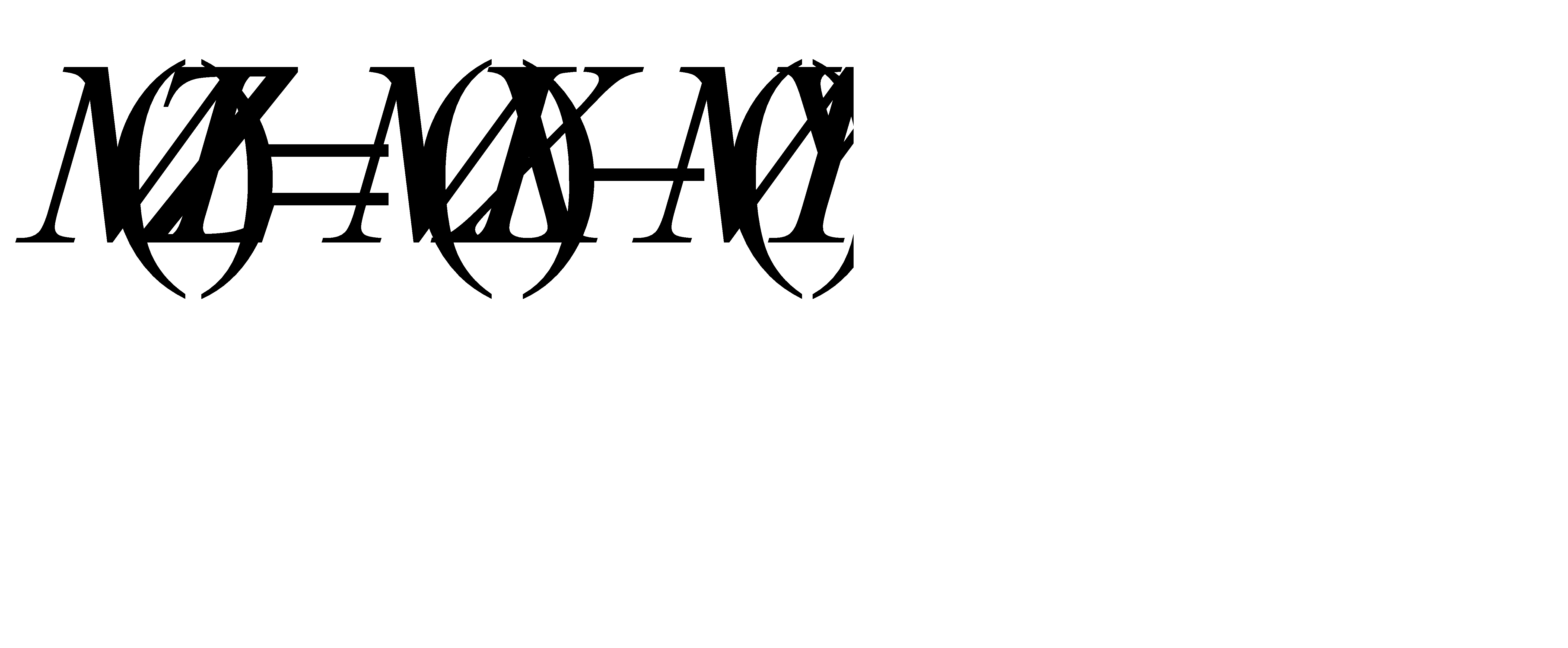Но так как 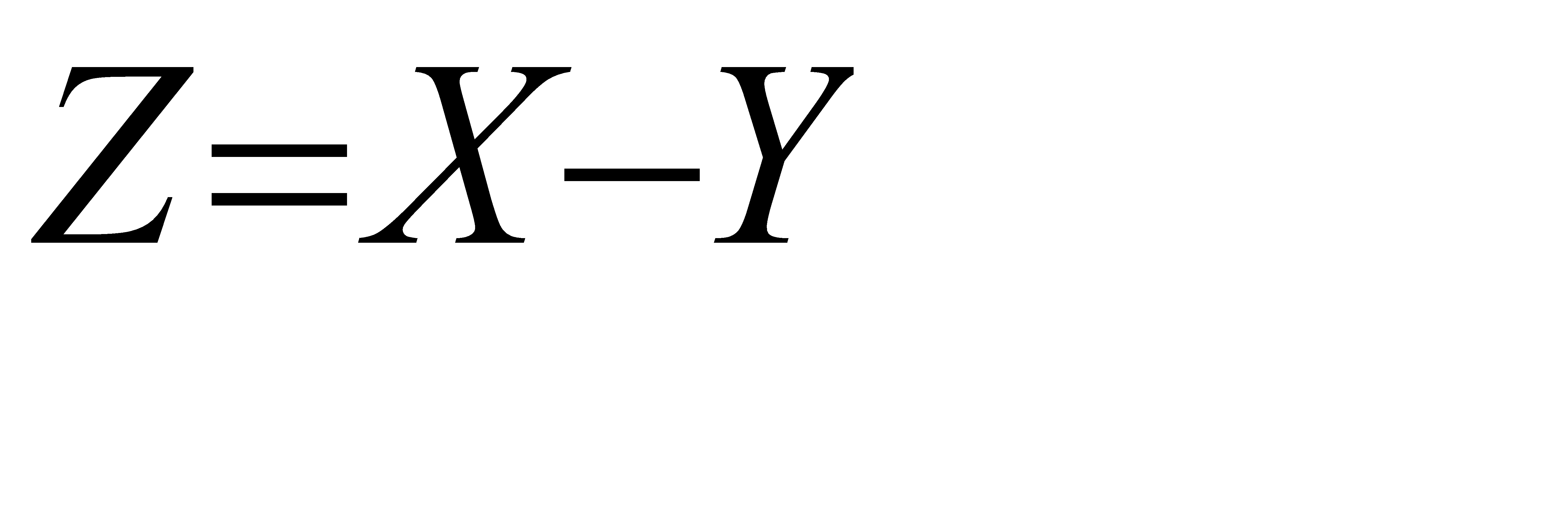, имеем

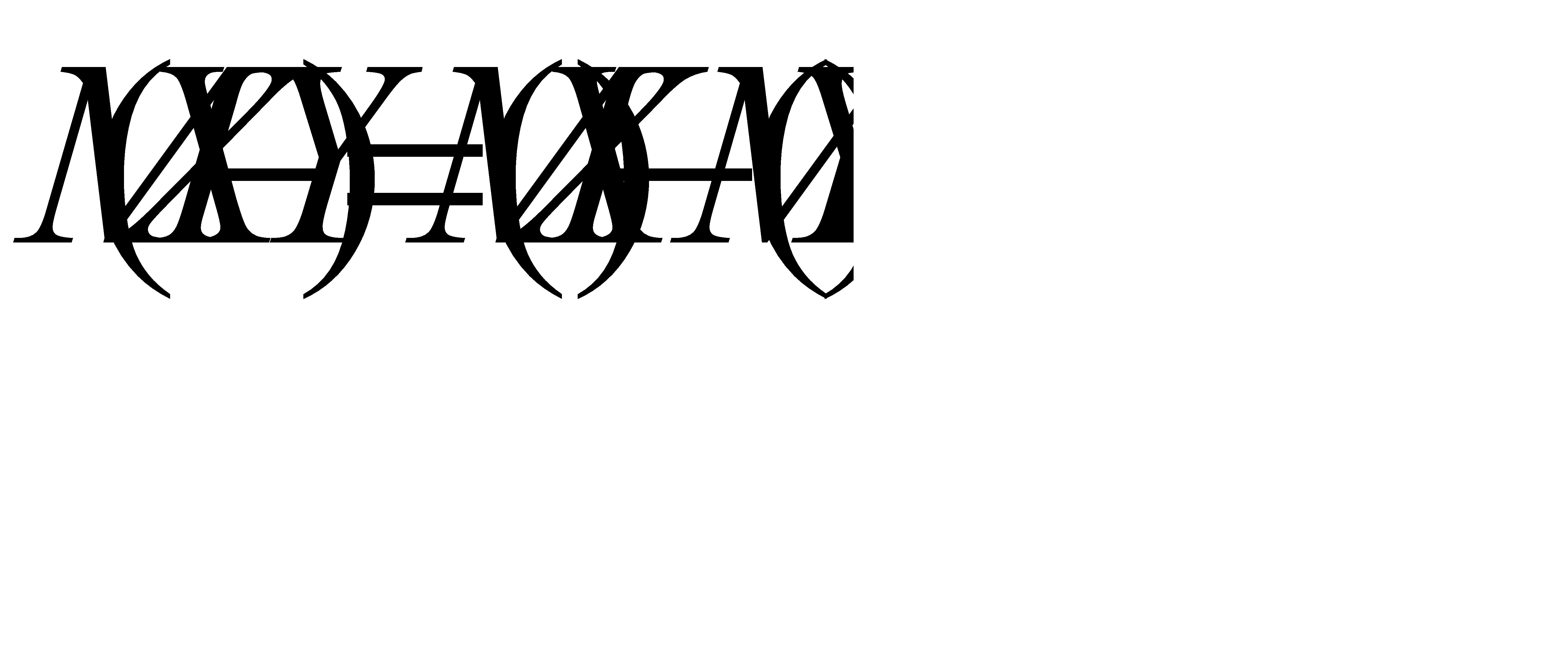, что и требовалось доказать.

б) Требуется доказать, что верно равенство 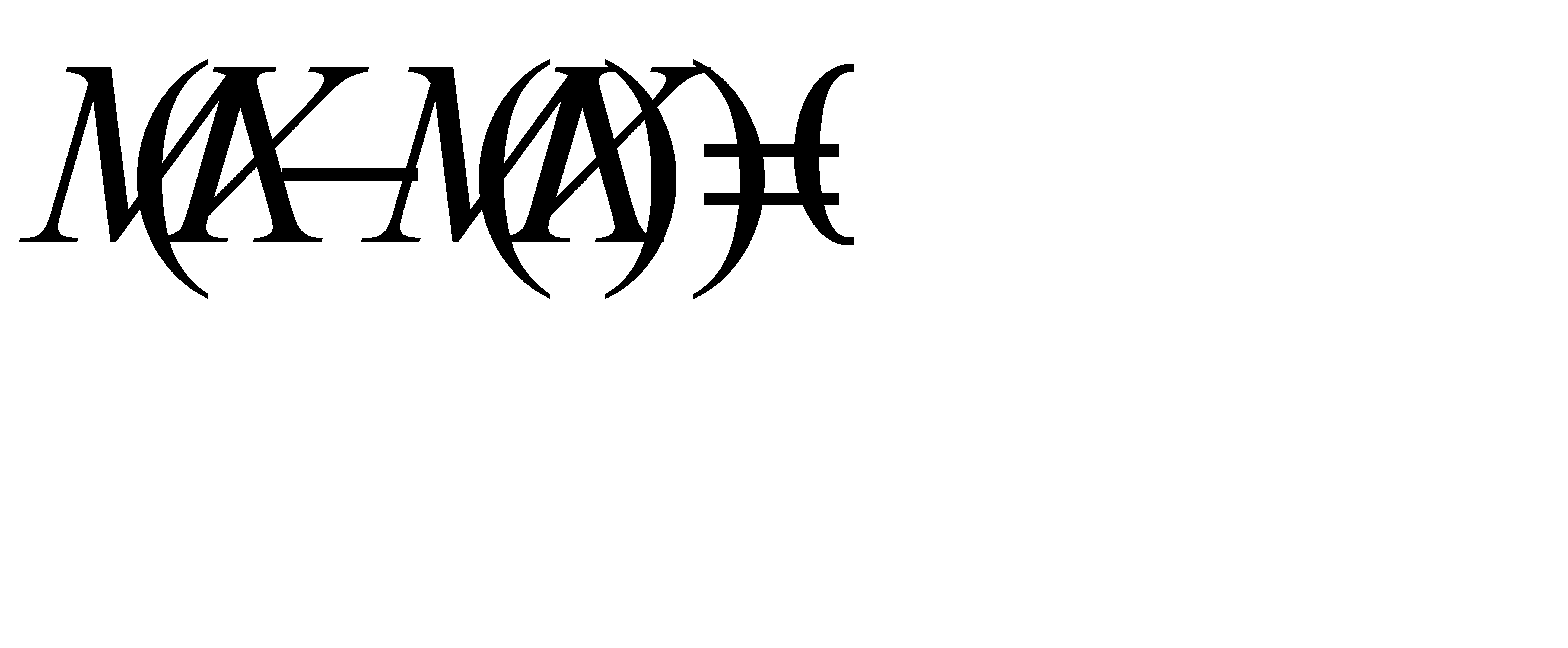. По формуле, доказанной в п. а), получаем .

Так как математическое ожидание 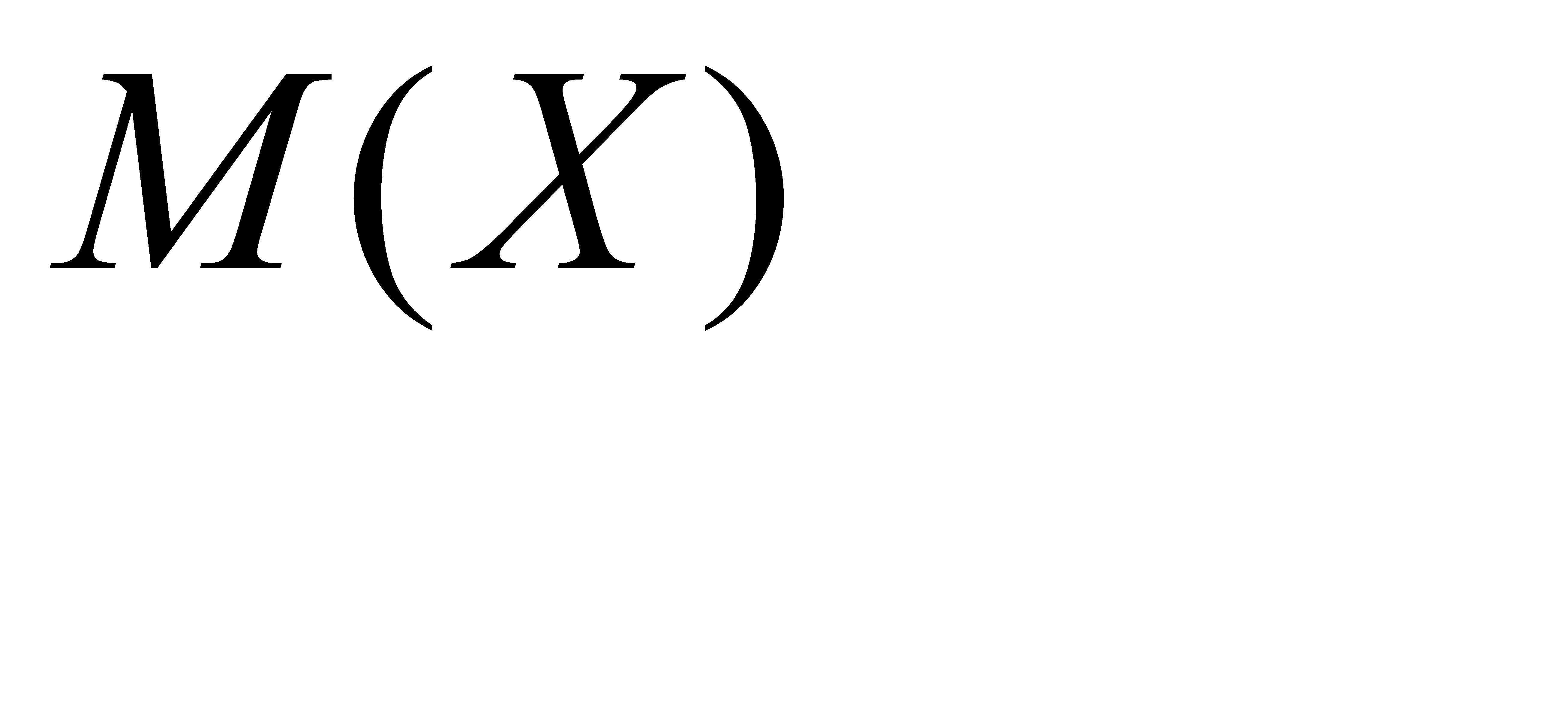есть постоянная, можно воспользоваться свойства 1 случайной величины: 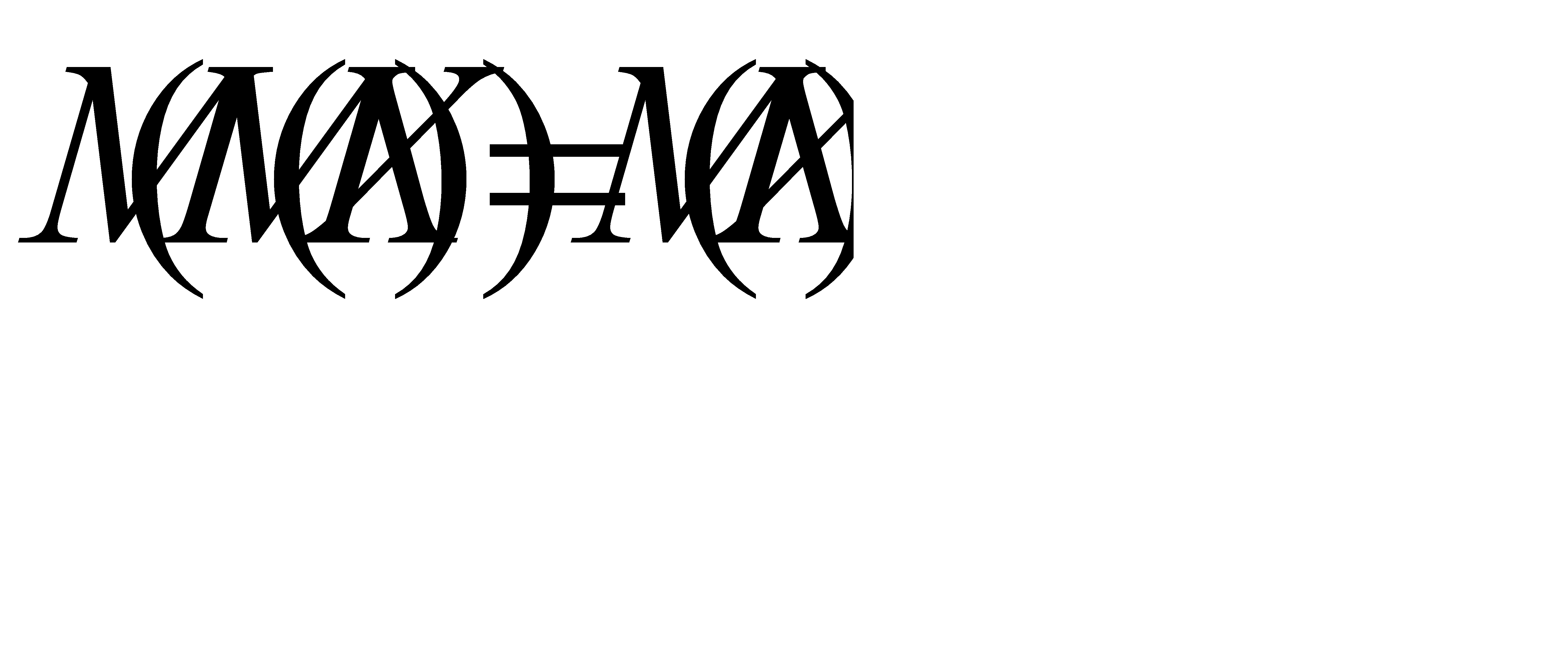. Теперь имеем

, что и требовалось доказать.

№191 Дискретная случайная величина X принимает три возможных значения: 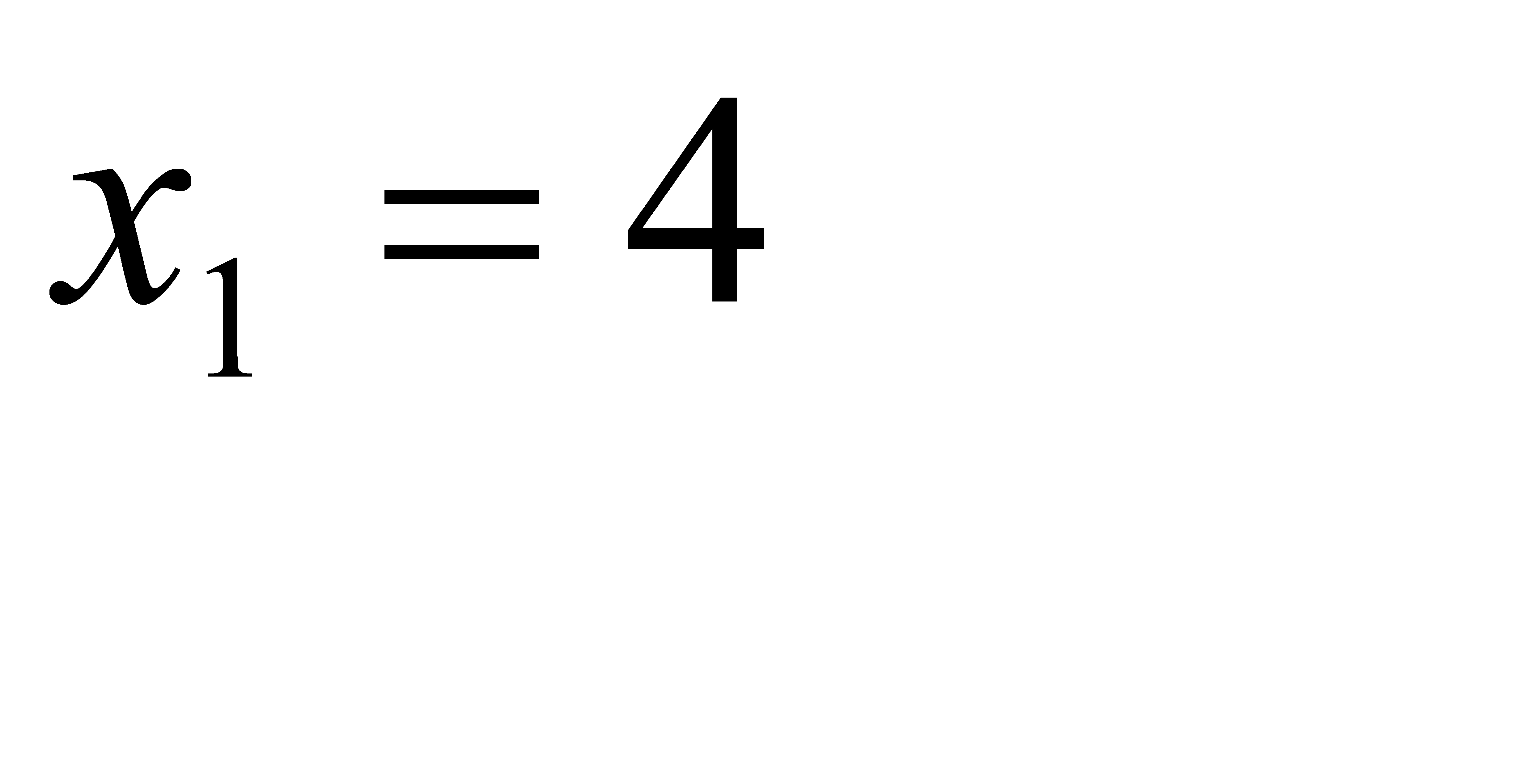с вероятностью 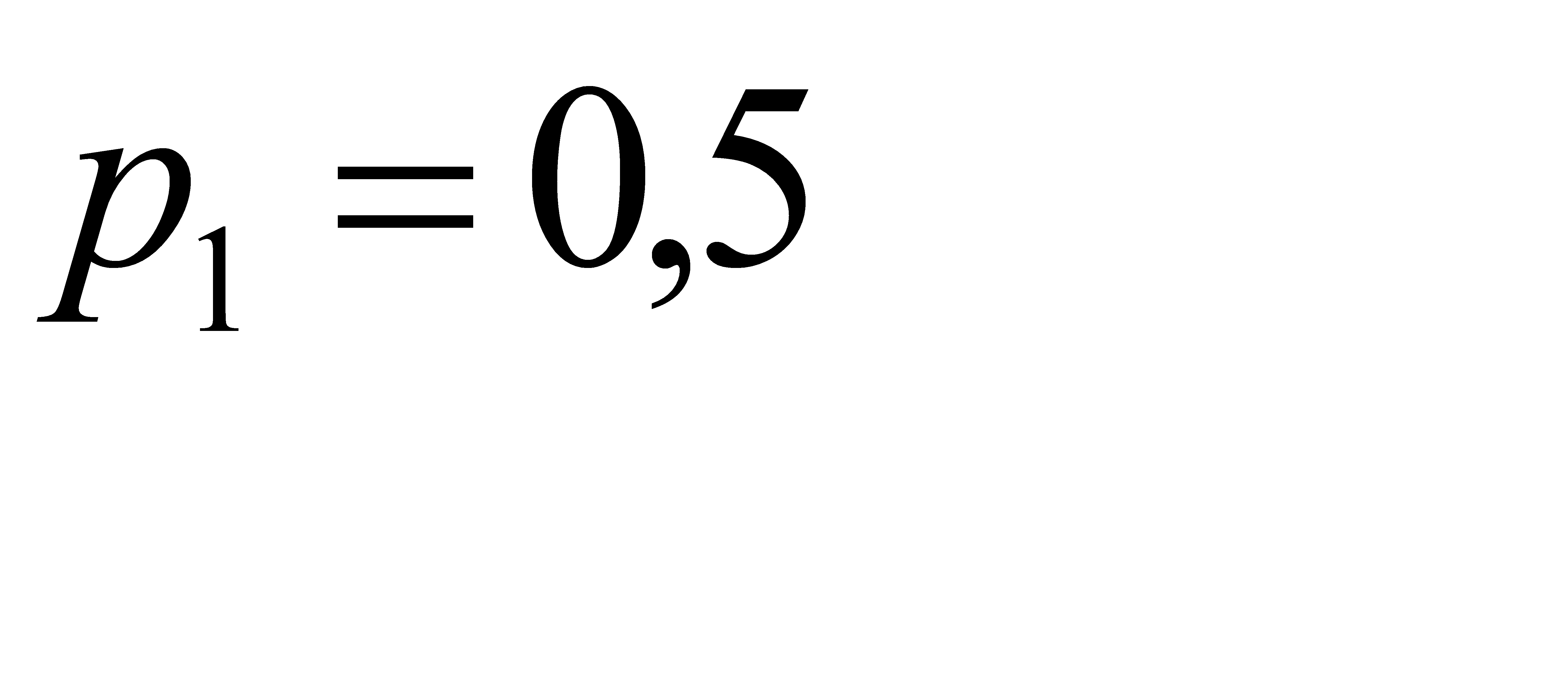; 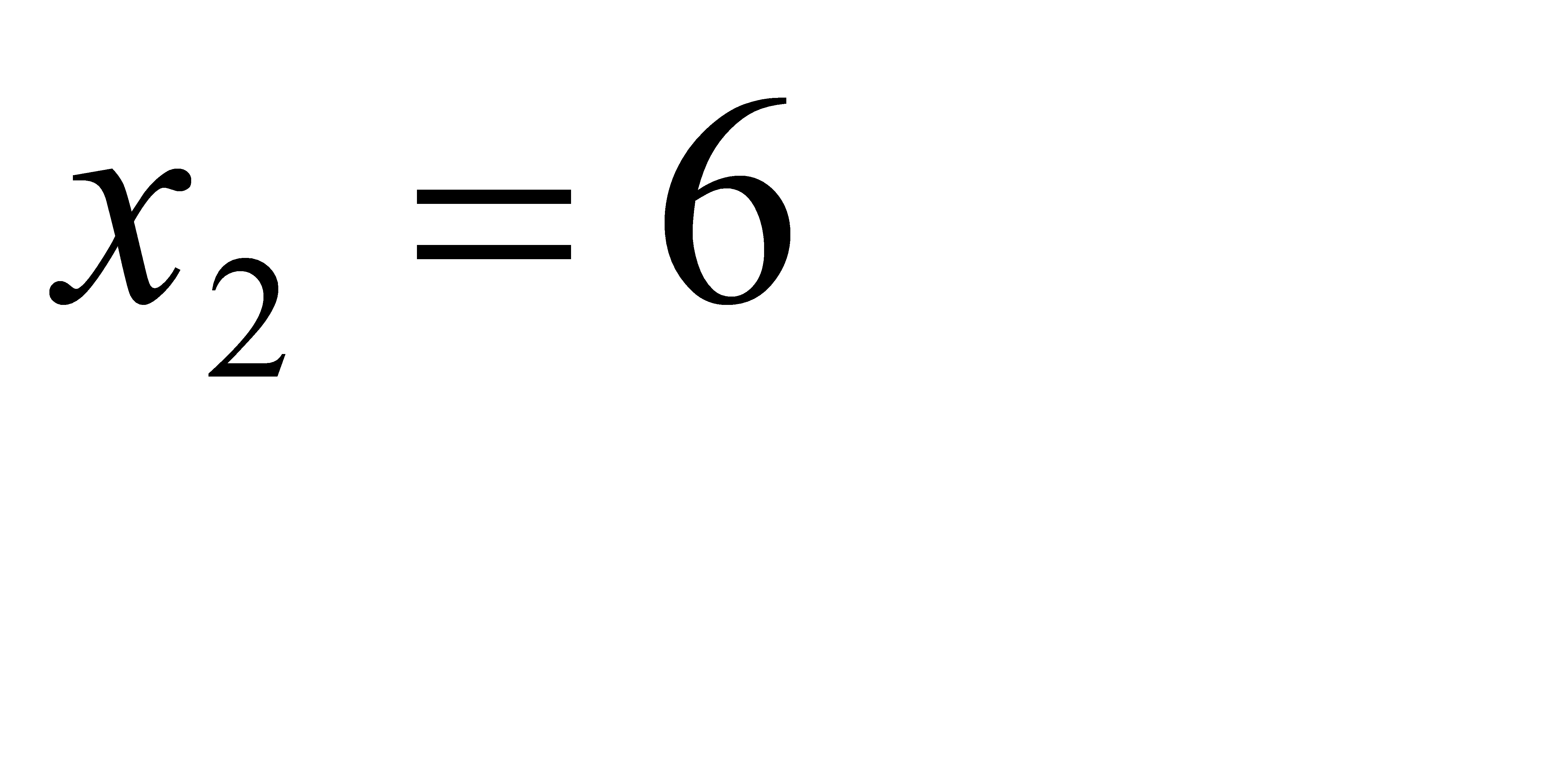с вероятностью 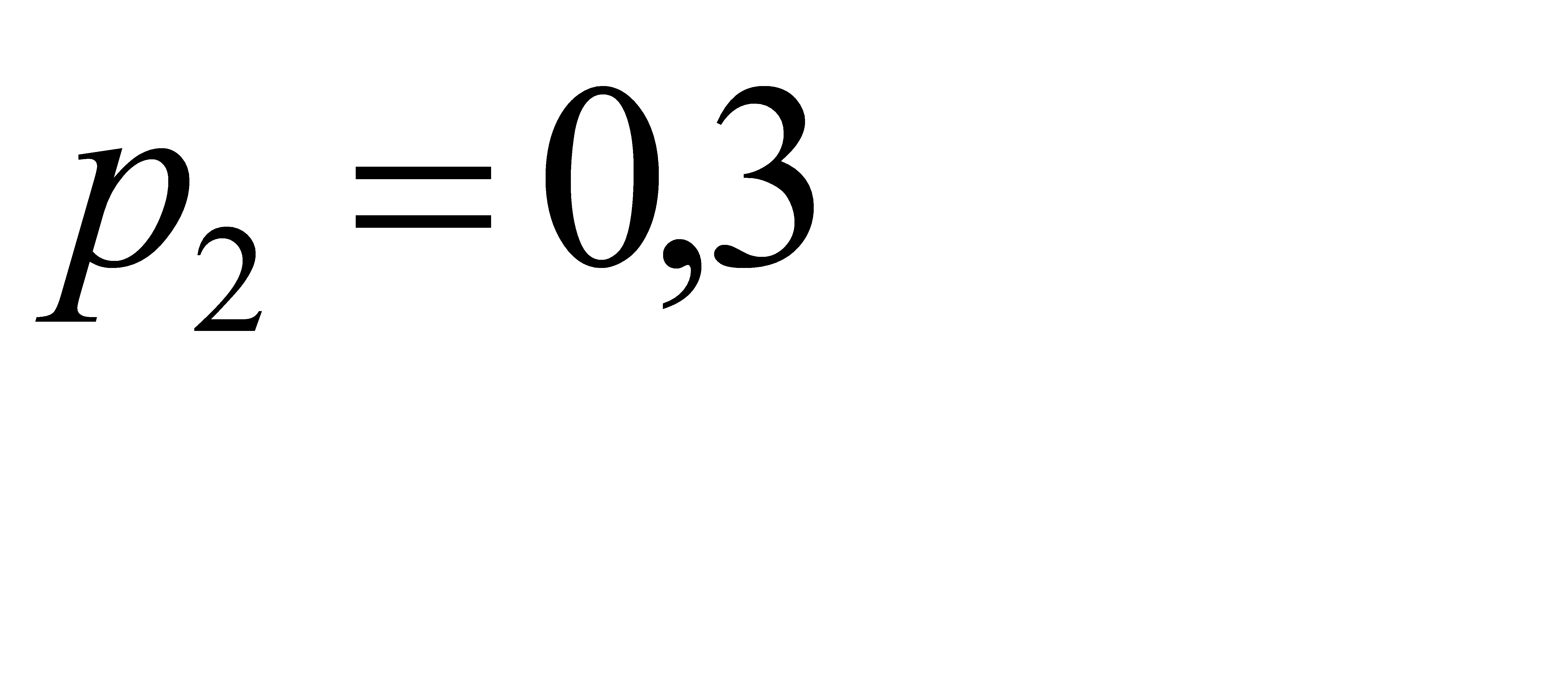и 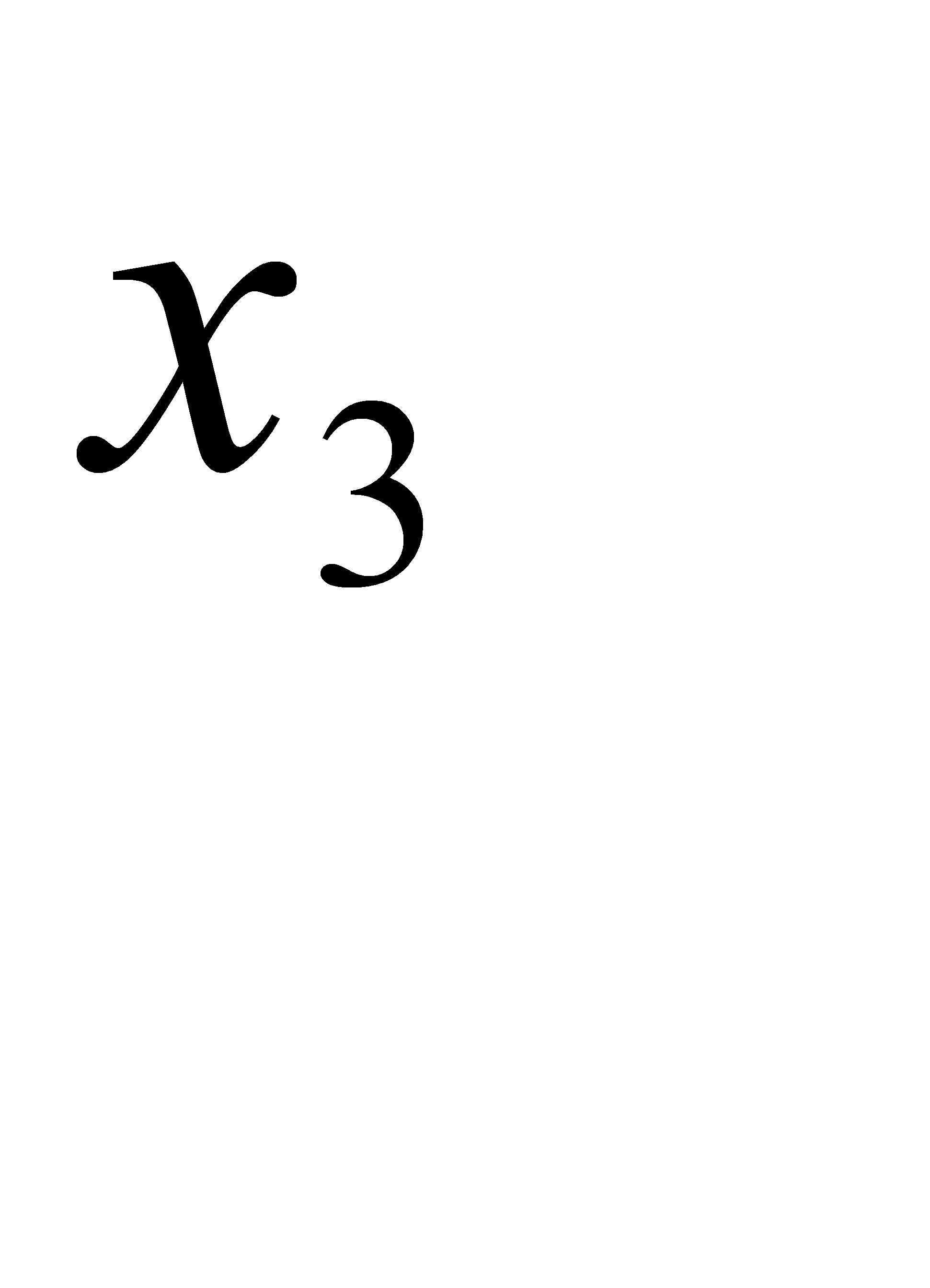с вероятностью 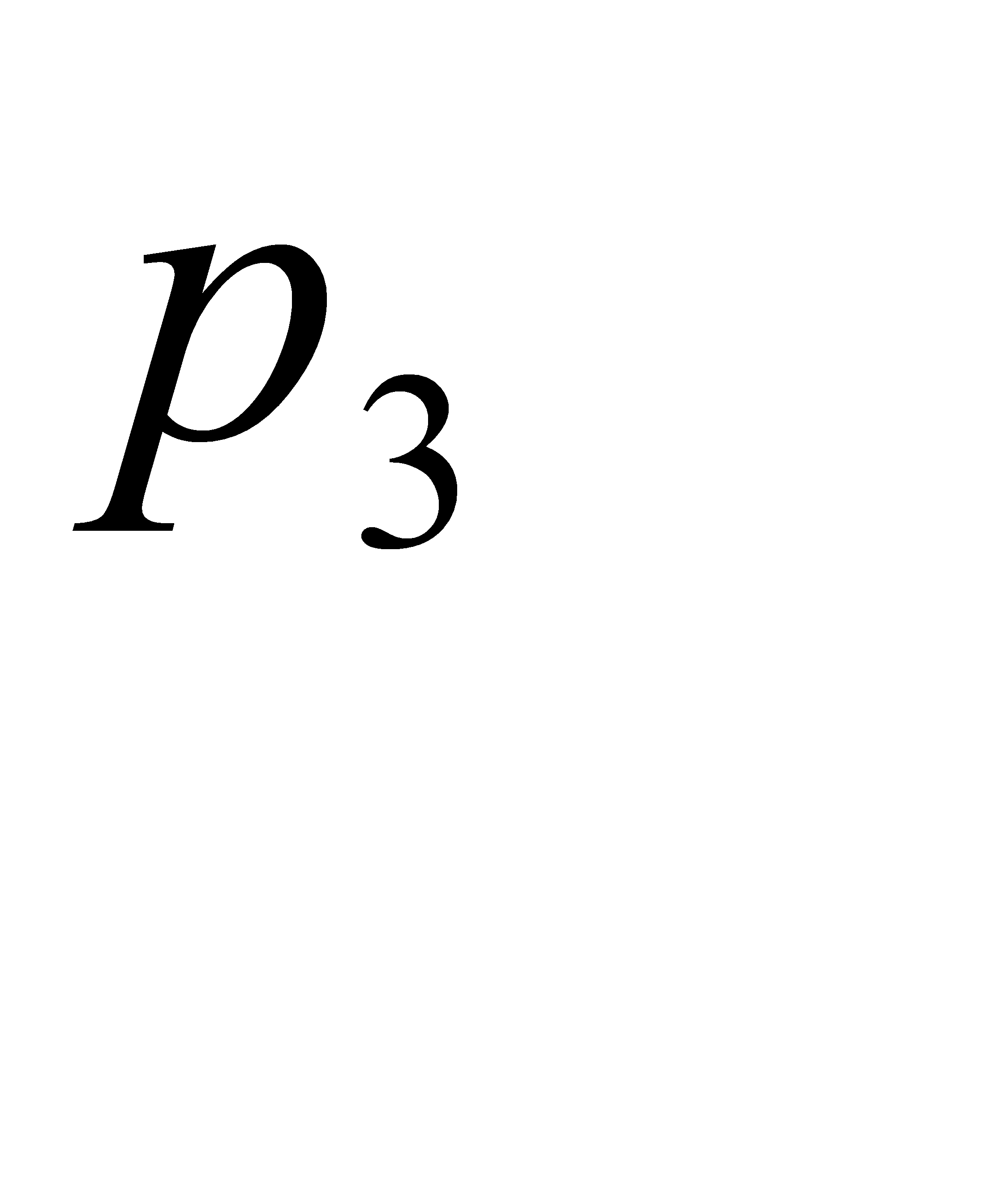. Найт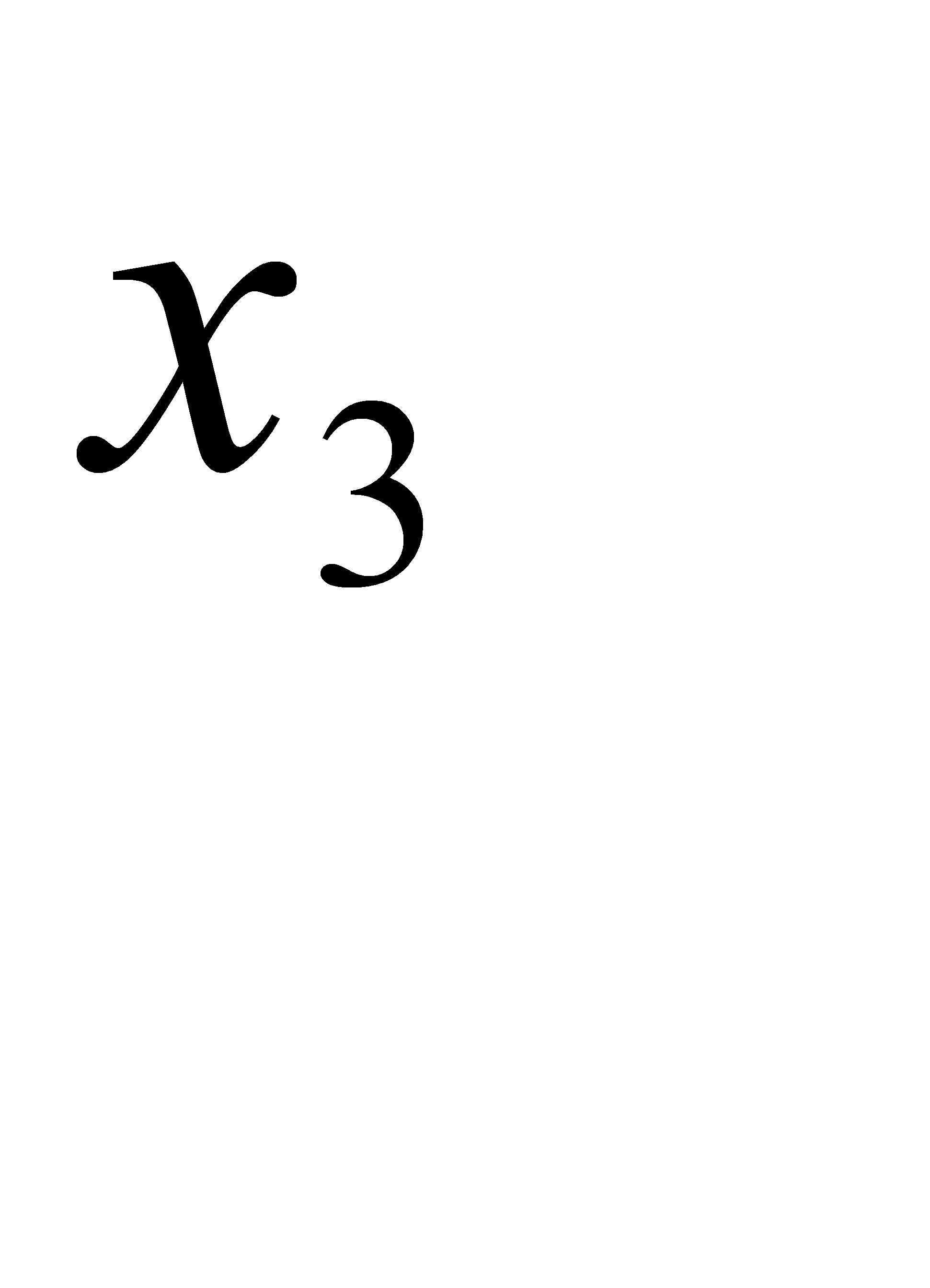и и 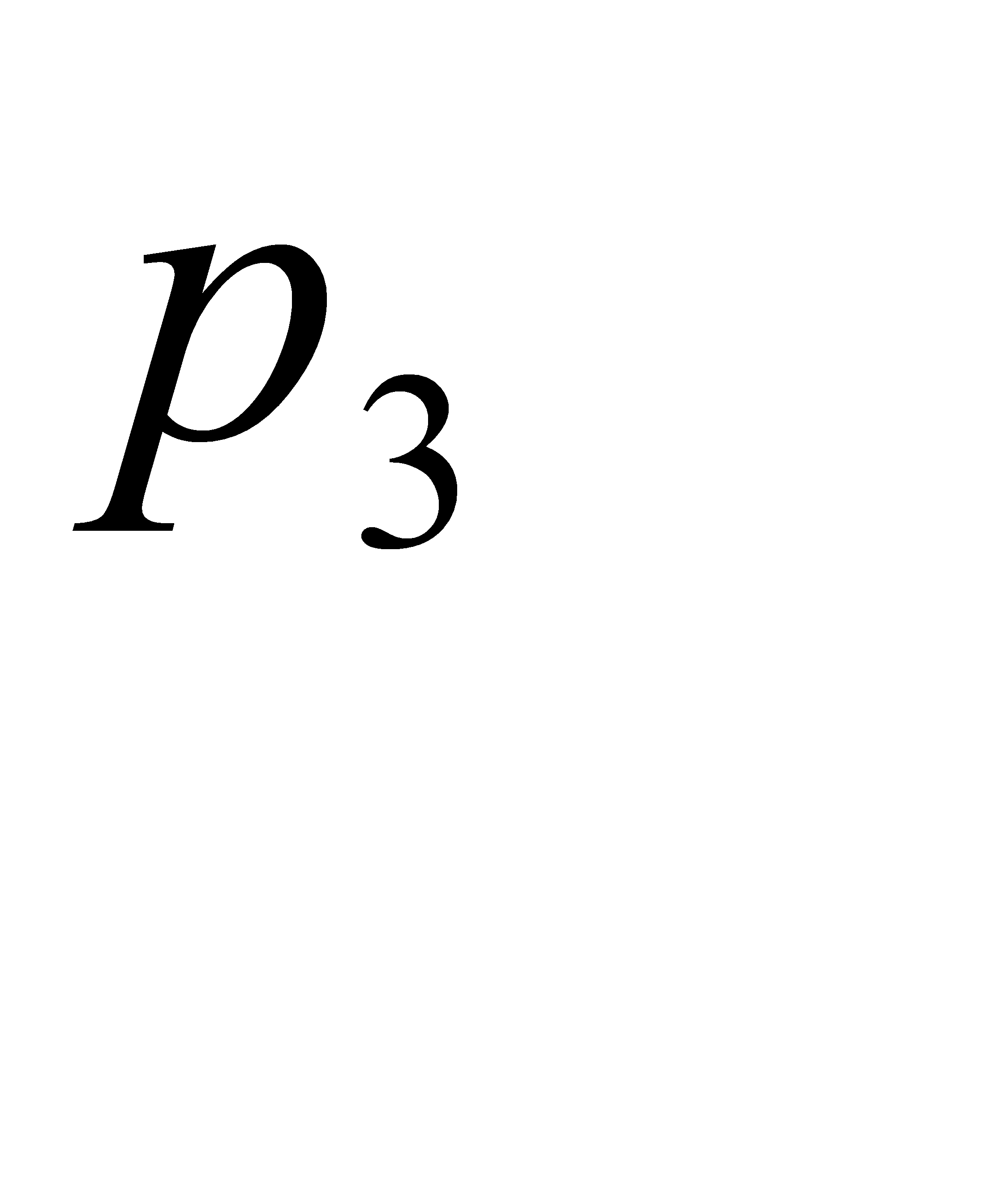, зная, что .

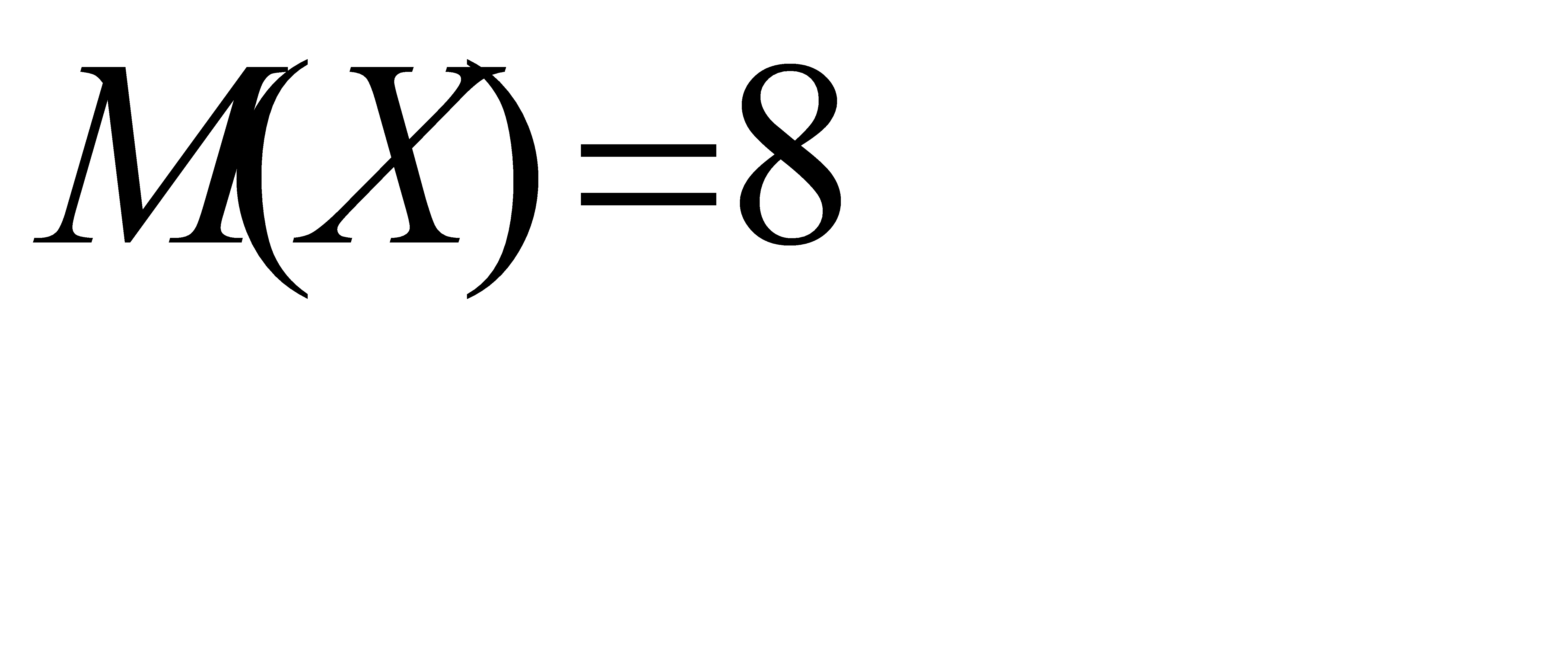Решение:

Поскольку случайная величина принимает одно из трёх возможных значений, они образуют полную группу. Тогда , .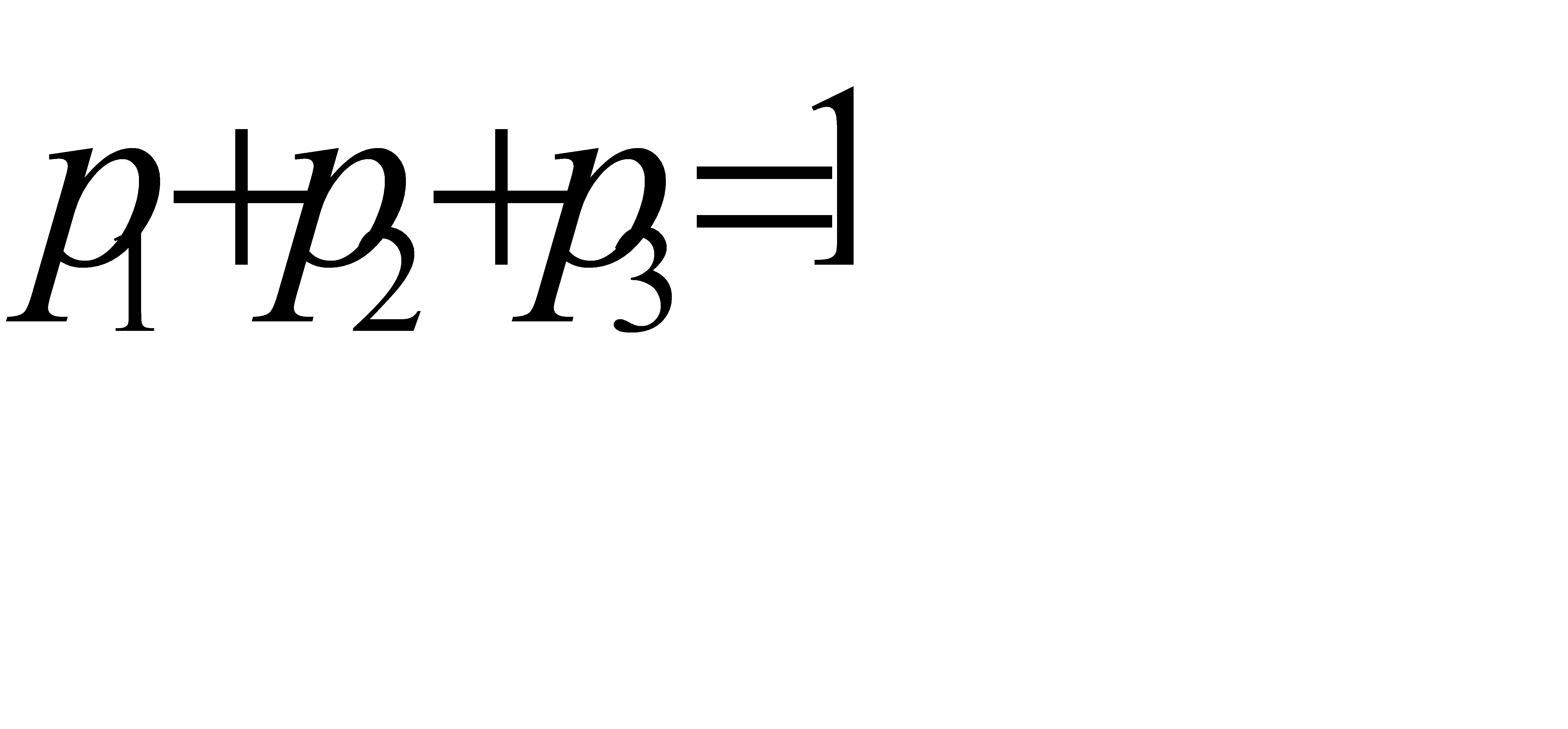

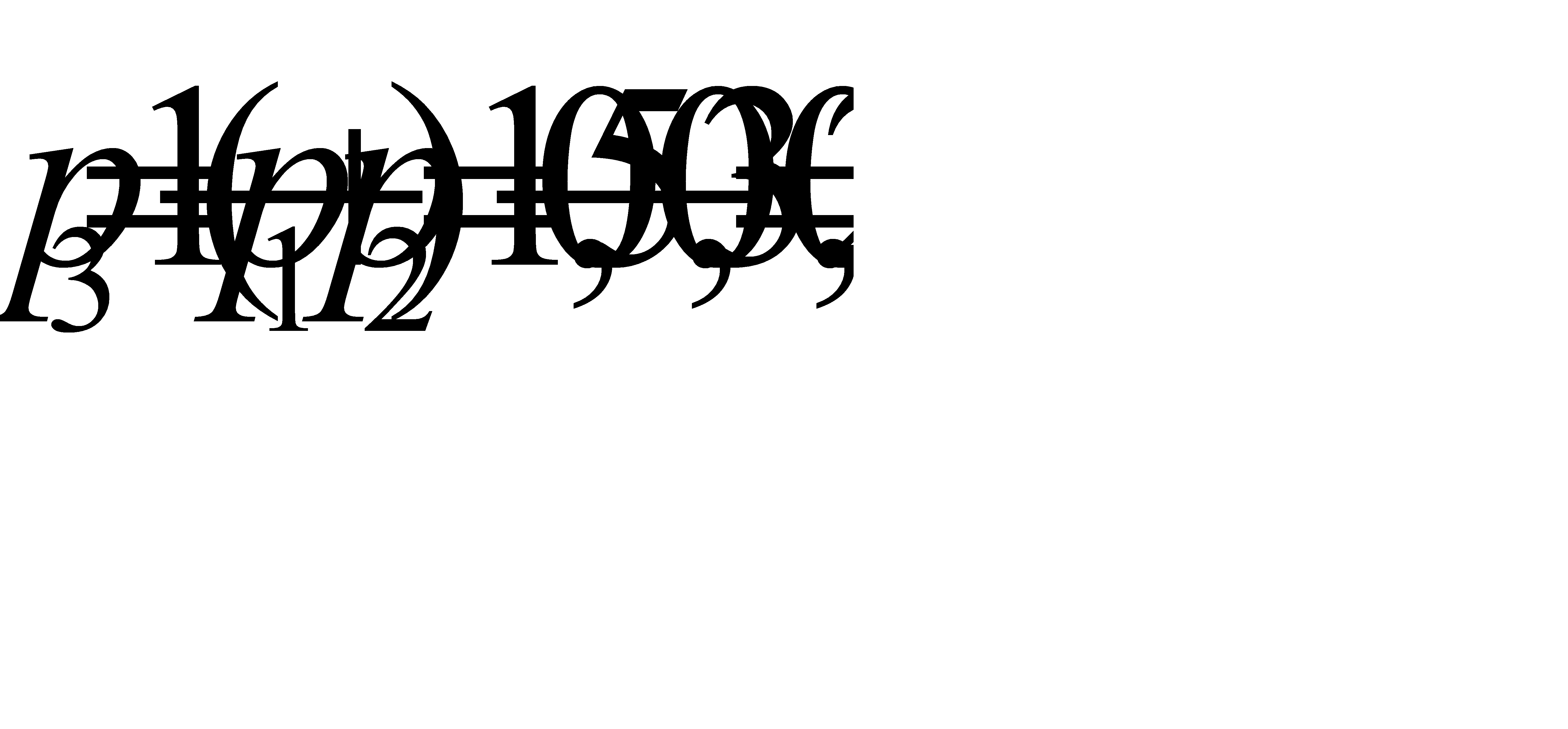Далее, из определения математического ожидания . Отсюда .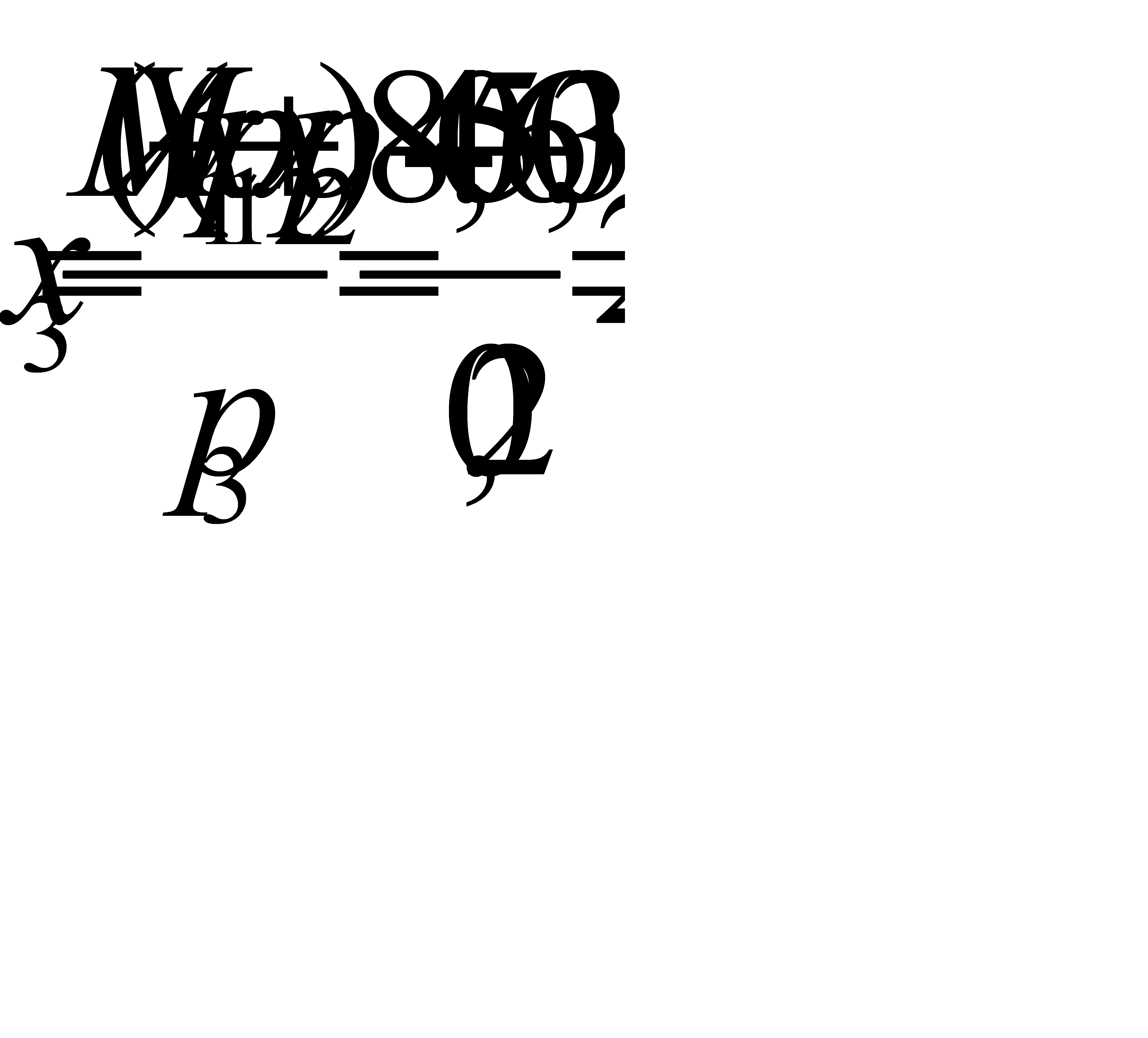

Ответ: 21.

№192 Дан перечень возможных значений дискретной случайной величины X: 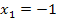, , 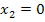, 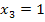а также известны математические ожидания этой величины и ее квадрата: 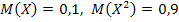. Найти вероятности 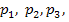соответствующие возможным значениям .

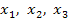Решение:

Так как сумма вероятностей всех возможных значений X равна 1, а 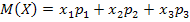и 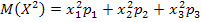, то составим систему уравнений.

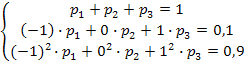
Решив ее, получим искомые вероятности: .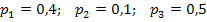

№193 Дан перечень возможных значений дискретной случайной величины 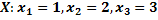, а так же известны математические ожидания этой величины и ее квадрата: .

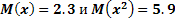Найти вероятности, соответствующие возможным значениям .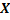

Решение:

Пользуясь тем, что сумма вероятностей всех возможных значений 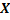равна единице, а так же принимая во внимание, что 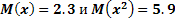, составим следующую систему трех линейных уравнений относительно неизвестных вероятностей:

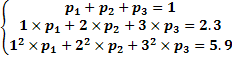
Решив эту систему, найдем искомые вероятности: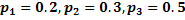

№194 В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание дискретной случайной величины X – числа нестандартных деталей среди двух отобранных.

Решение:

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь две детали из десяти деталей, т.е. 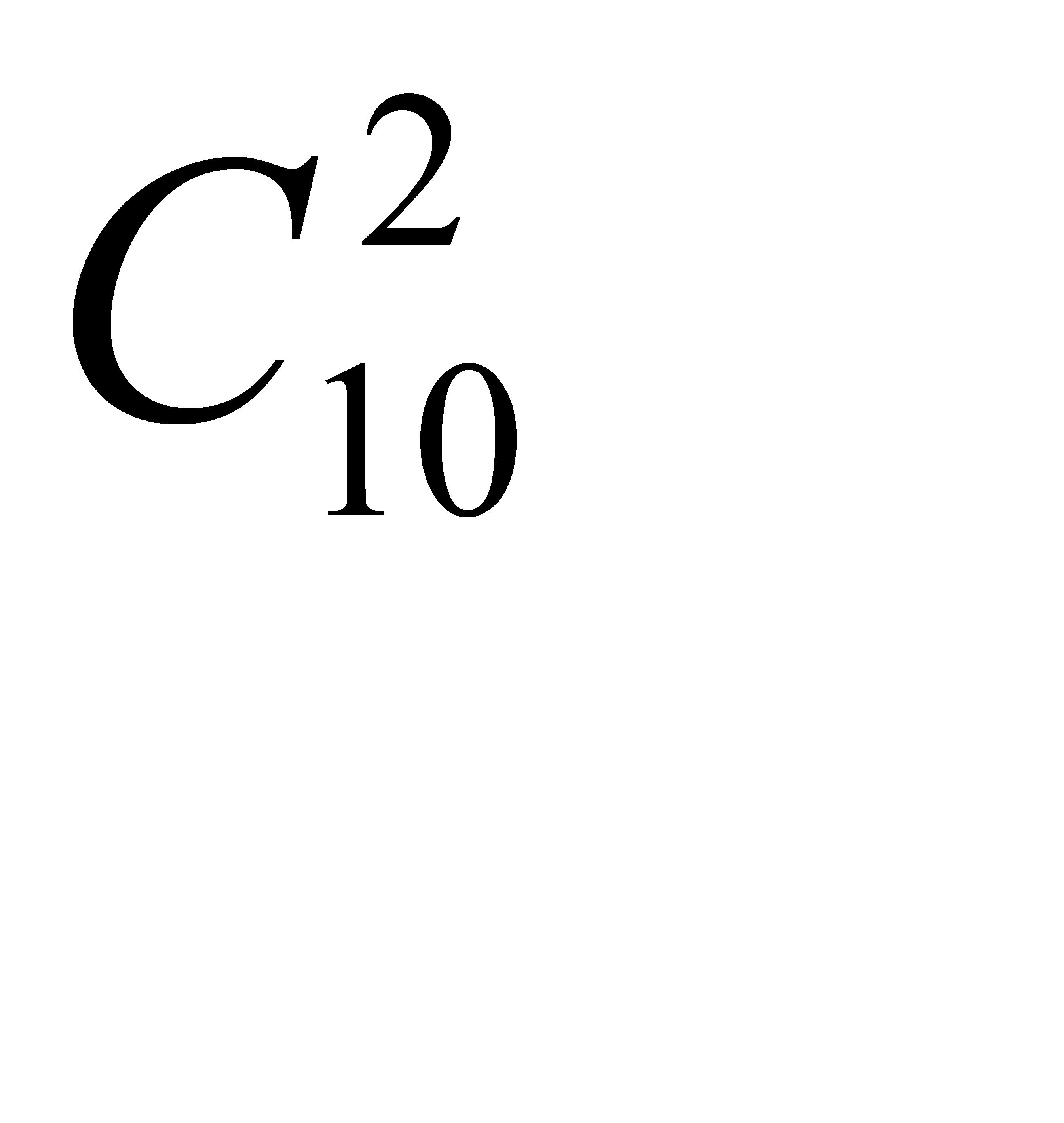- числу сочетаний из десяти по два.

А) одну нестандартную деталь можно взять из трех нестандартных деталей 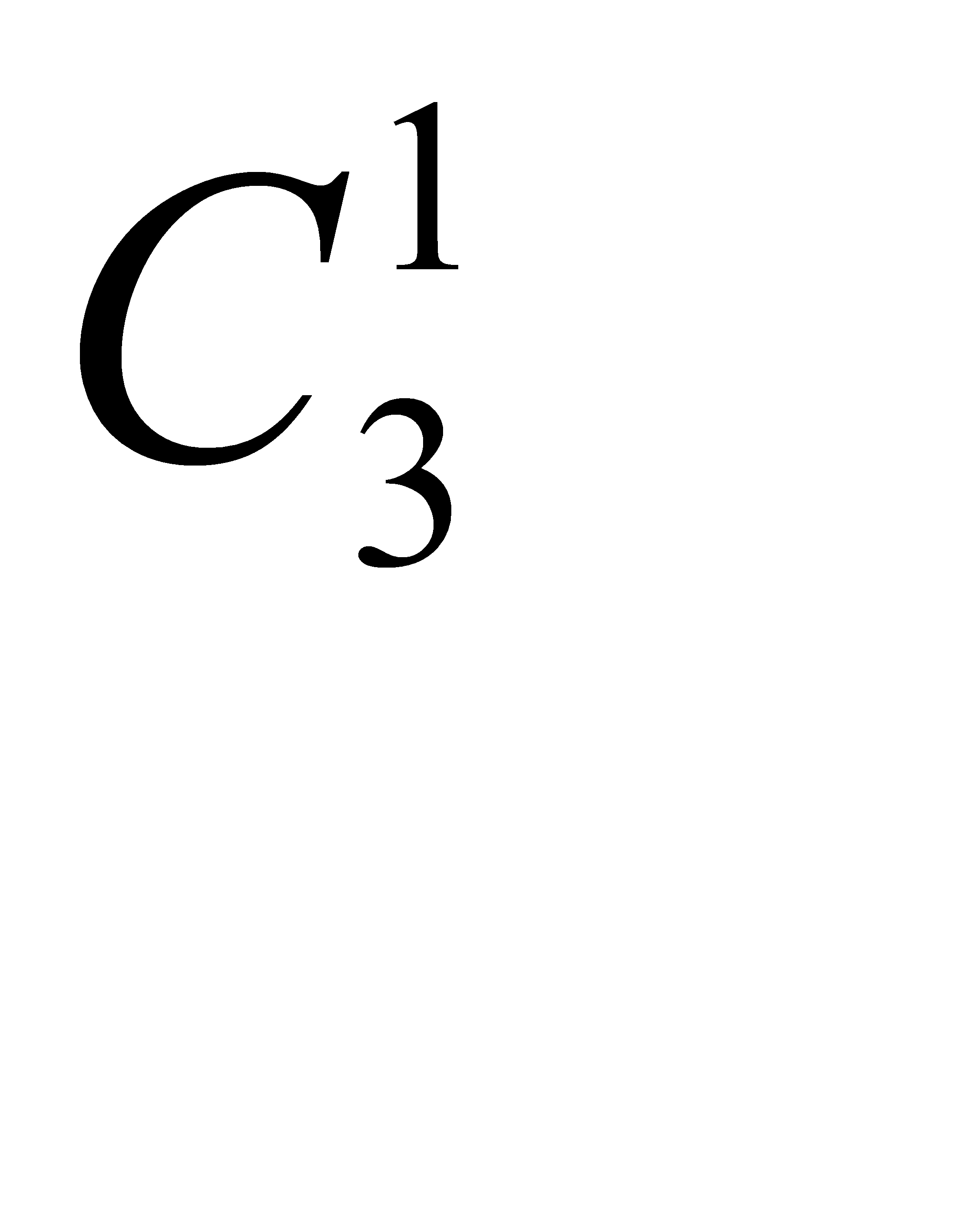способами; при этом одна деталь должна быть нестандартной; взять же одну нестандартную деталь из семи нестандартных можно 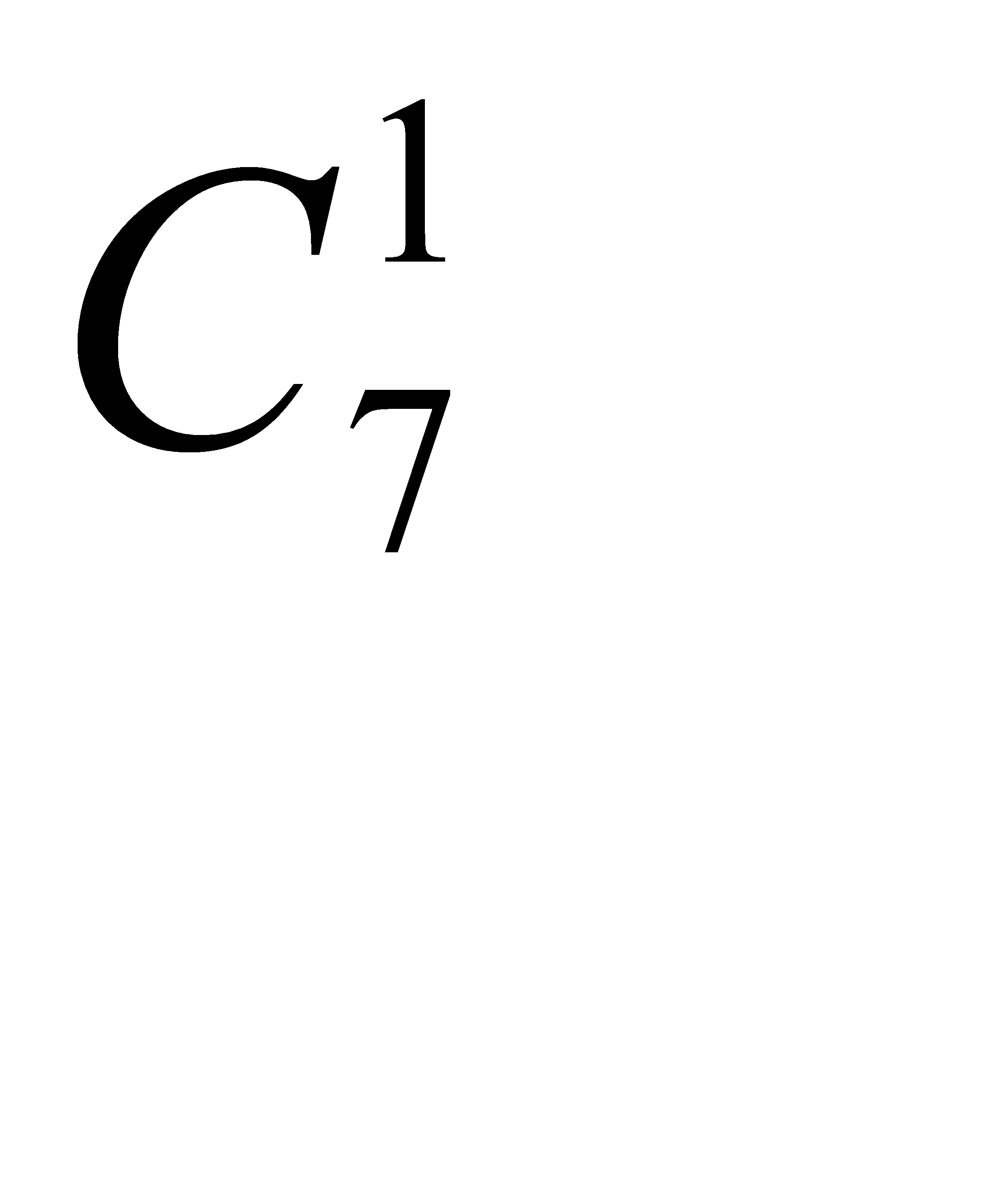способами. Следовательно, число благоприятствующих исходов равно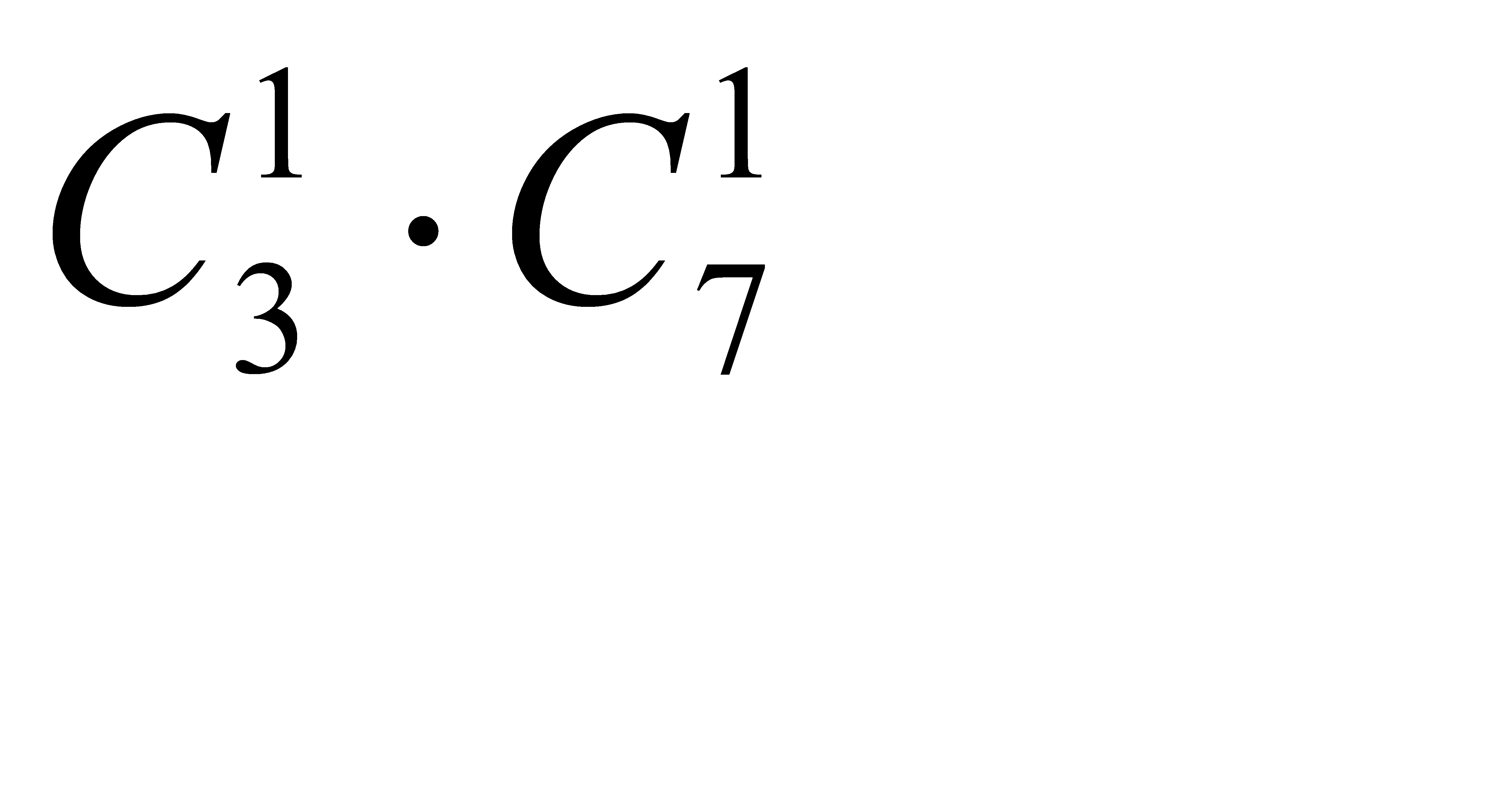

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

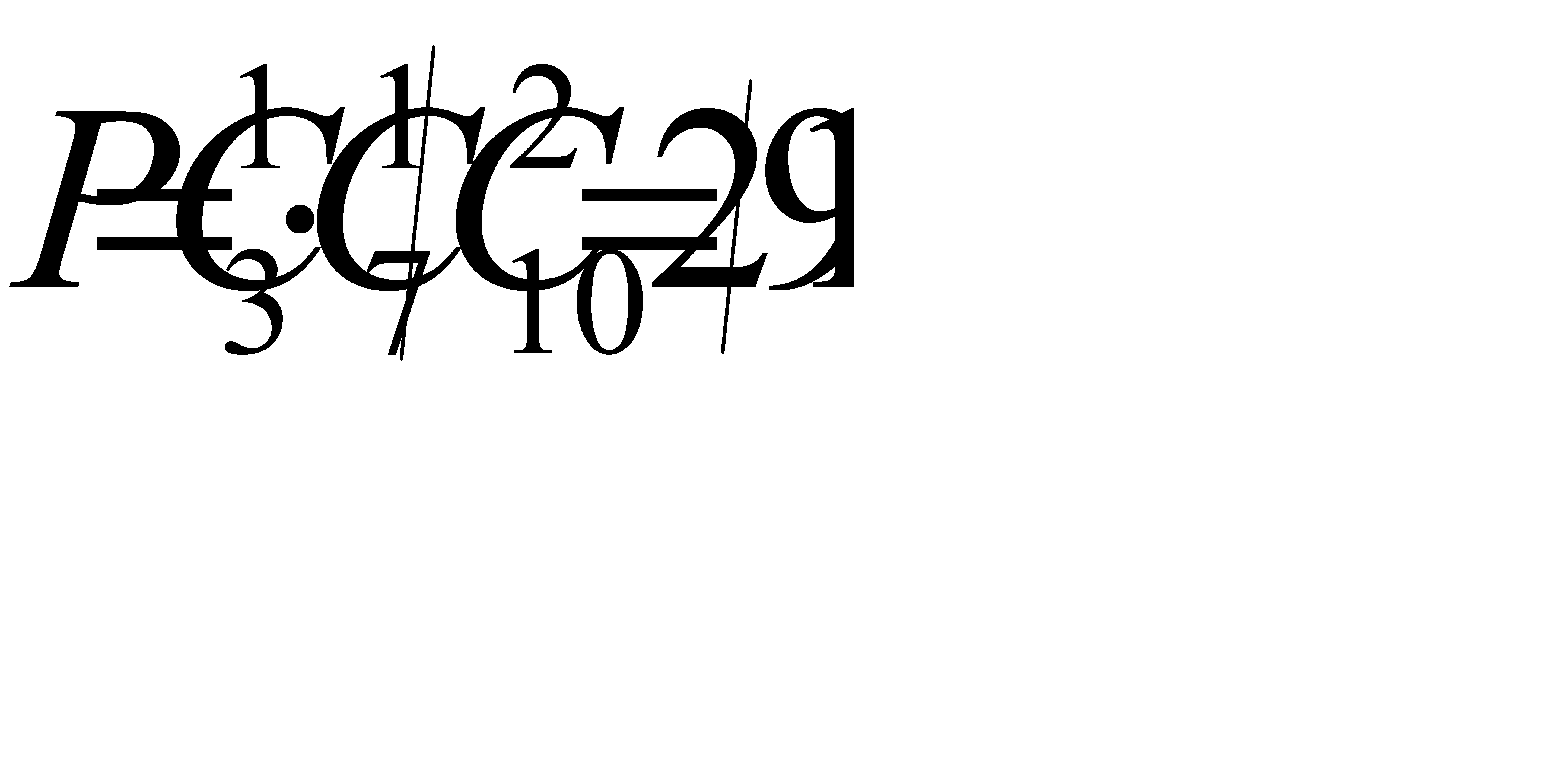
Две нестандартных детали можно взять из трех нестандартных деталей 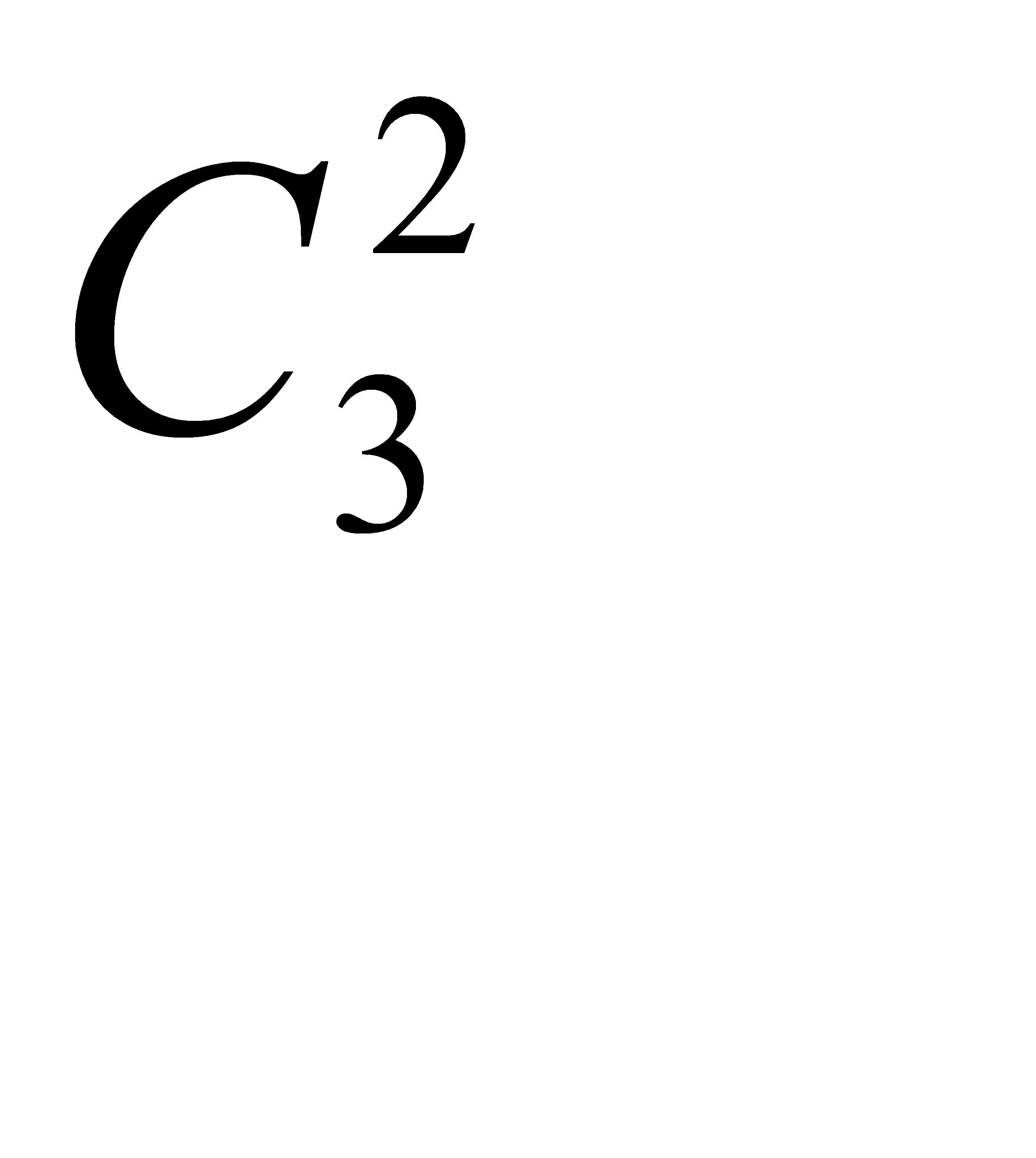способами; Следовательно, число благоприятствующих исходов равно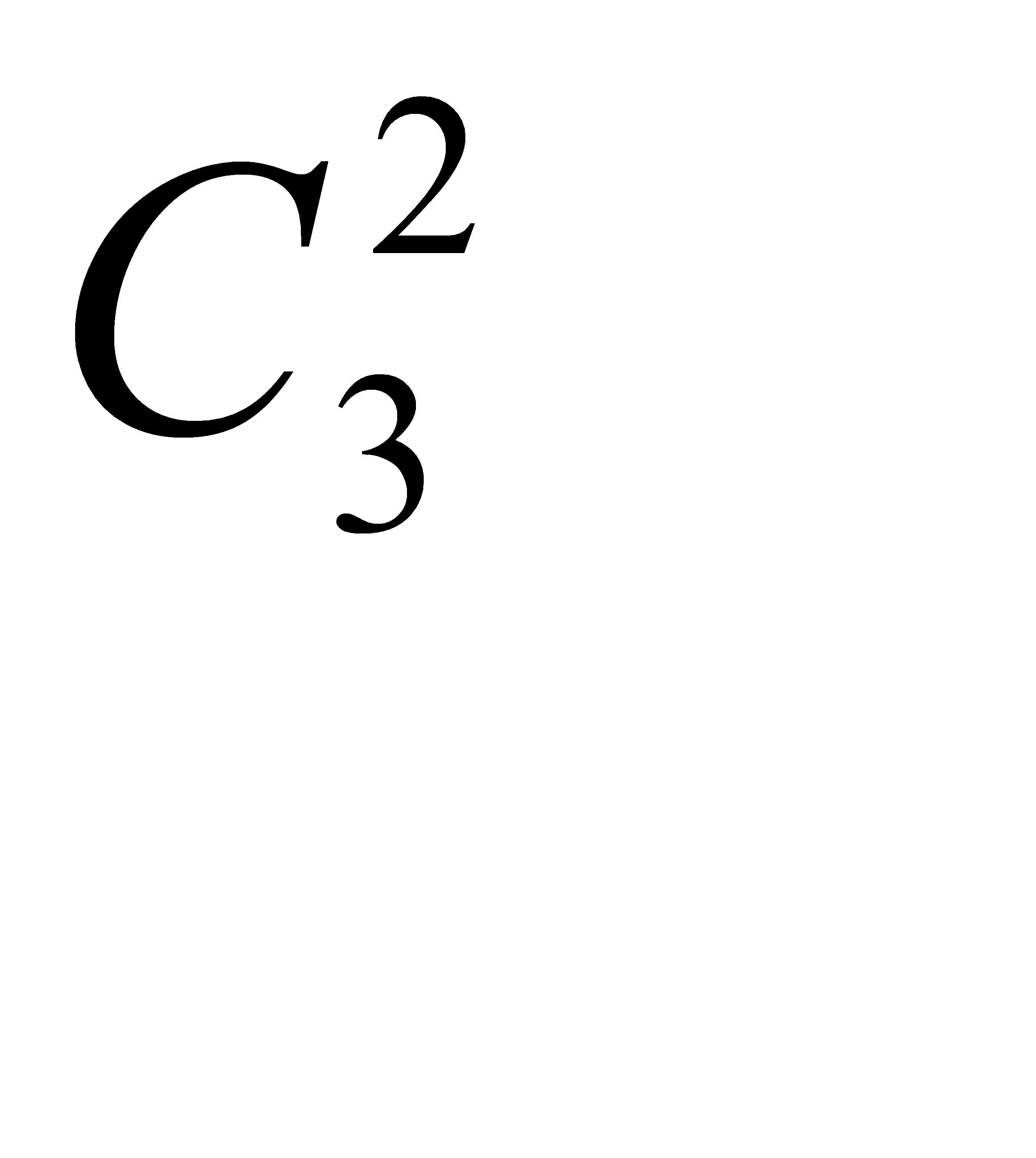

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:

№195 а) Доказать, что математическое ожидание числа появлений события А в одном испытании равно вероятности р появления события А.

Указание. Дискретная случайная величина X—число появлений события в одном испытании—имеет только два возможных значения: x = l (событие А наступило)

и y = 0 (событие А не наступило).

б) Доказать, что математическое ожидание дискретной случайной величины X—числа появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события равна р—равно произведению числа испытаний на вероятность появления события в одном испытании, т. е. доказать, что математическое ожидание биномиального распределения М(Х)=nр.

Решение:

а) дискретная случайная величина х задана законом распределения:

х 1 2

р р р

По формуле математического ожидания 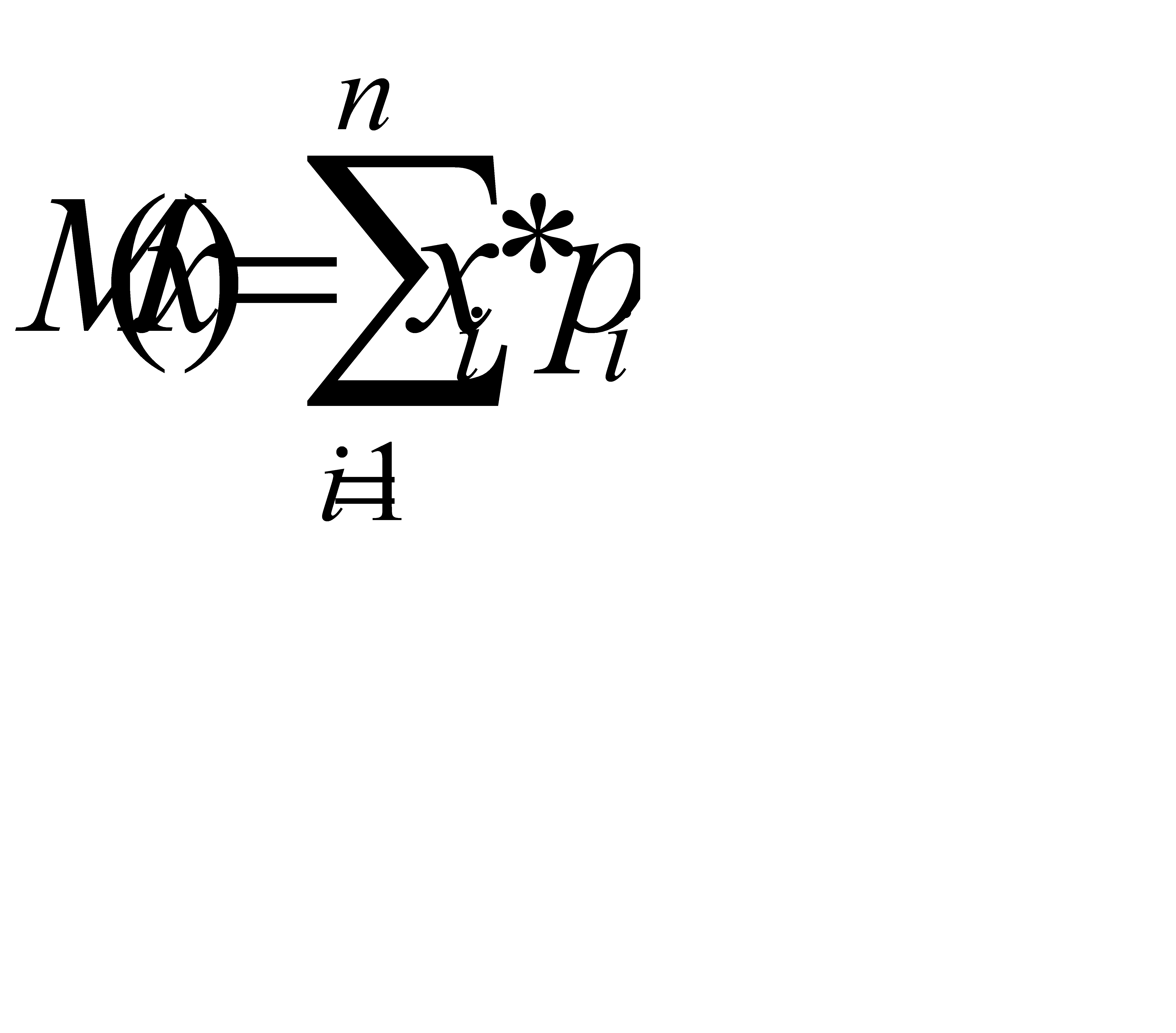получим:

М(х)=1*р+0*р=р

Что и требовалось доказать.

б) Так как число испытаний велико, а вероятность р появления со-

бытия в каждом испытании очень мала, то воспользуемся законом Пуассона.

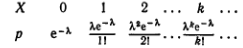
По определению математического ожидания для

случая, когда число возможных значений X есть счетное множество,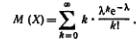

Учитывая, что при к=0 первый член суммы равен нулю, при-

примем в качестве наименьшего значения k единицу:

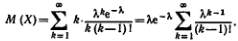
Положив k—l=m, получим

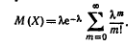
Принимая во внимание, что

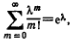получим:

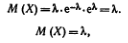
А так как λ=np то получим M(x)=np что и требовалось доказать.

№196 Найти математическое ожидание дискретной случайной величины Х – числа таких бросаний пяти игральных костей, в каждом из которых на двух костях появится по одному очку, если общее число бросаний равно двадцати.

Решение:

Воспользуемся формулой 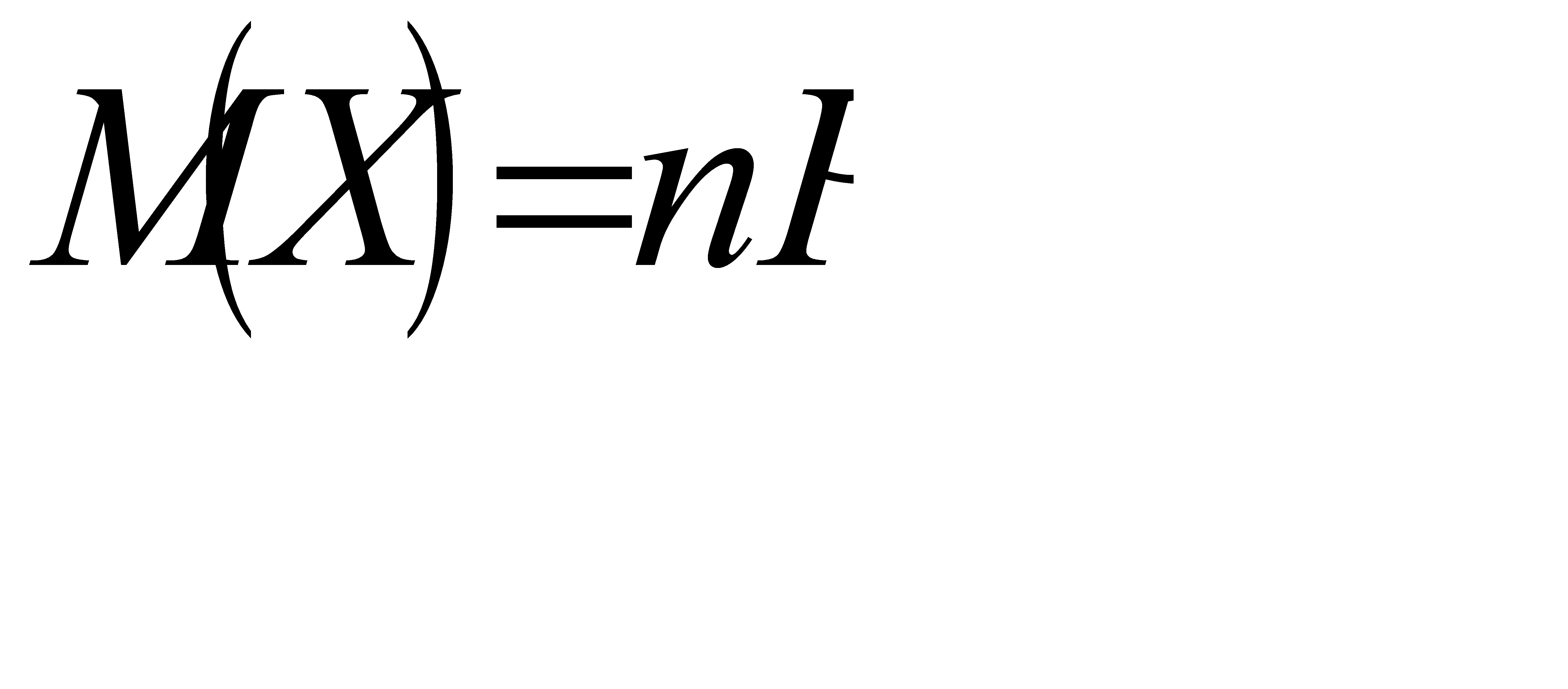, где n – общее число испытаний (бросаний пяти костей); Х – число появлений интересующего нас события (на двух костях из пяти появится по одному очку) в n испытаниях; Р – вероятность появления рассматриваемого события в одном испытании.

По условию, n = 20. Остаётся найти Р – вероятность того, что на гранях двух из пяти костей появится по одному очку. Эту вероятность вычислим по формуле Бернулли, учитывая, что вероятность появления одного очка на грани одной кости p = 1/6, следовательно q = 5/6:

.

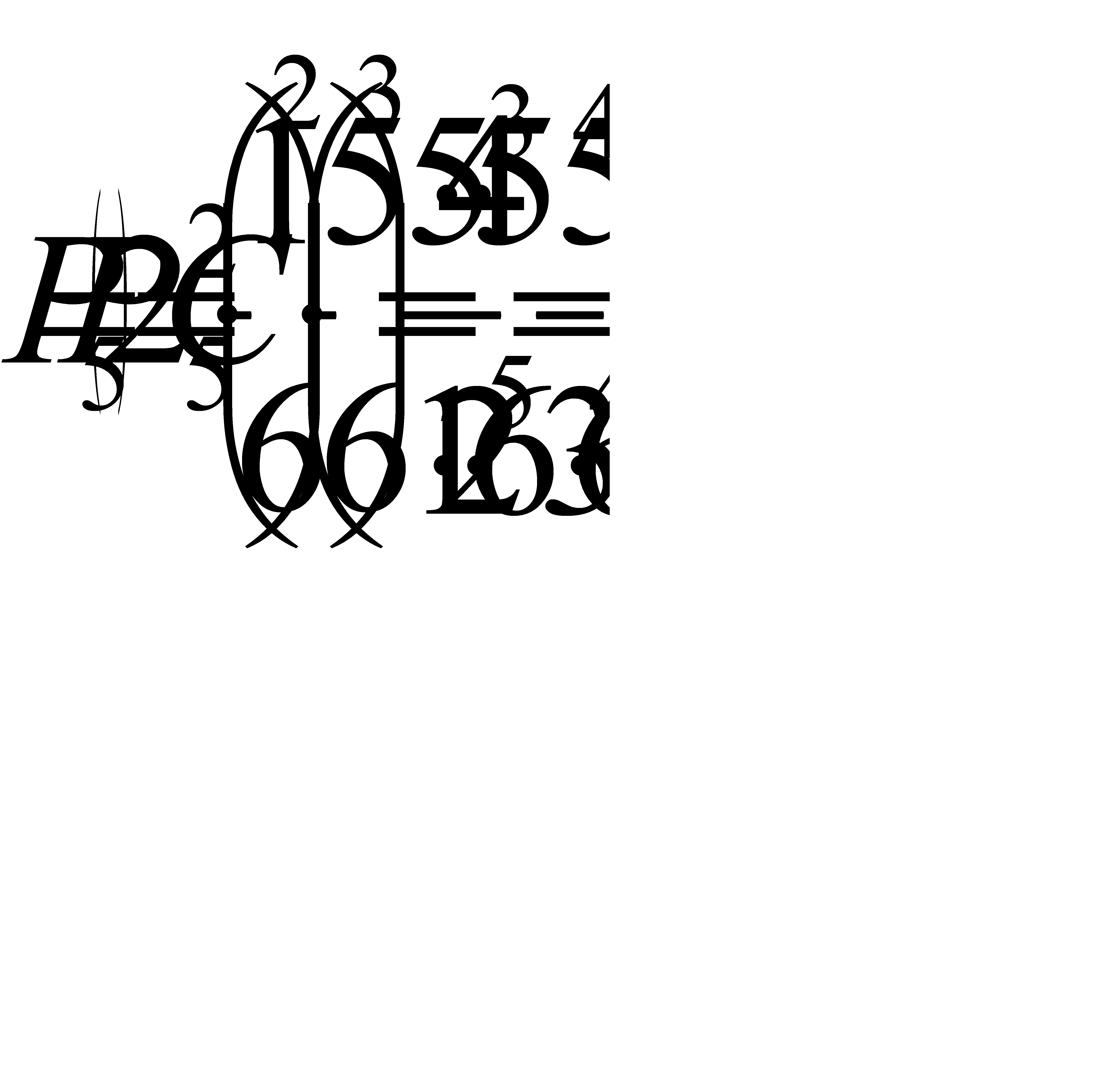Искомое математическое ожидание

Ответ: 3

Прокаева Наталия

Устройство состоит из элементов. Вероятность отказа любого элемента за время опыта равна . Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно элементов, если всего произведено опытов. Предполагается, что опыты независимы один от другого.

Решение:

Обозначим через 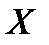число опытов, в которых откажет ровно 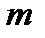элементов. Так как опыты независимы и вероятности интересующего нас события (в одном опыте откажет ровно 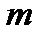элементов) в этих опытах одинаковы, то применима формула

(*)

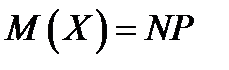где ­­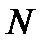— общее число опытов; 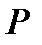— вероятность того, что в одном опыте откажет ровно 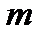элементов. Найдем вероятность 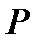по формуле Бернулли:

(**)

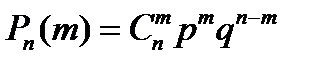Подставив (**) в (*), получим искомое математическое ожидание:

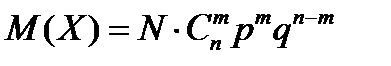
Бросают игральных костей. Найти метематическое ожидание числа таких бросаний, в каждом из которых выпадет ровно шестерок, если общее число бросаний равно .

Решение:

Воспользуемся формулой

,

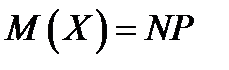Где 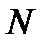– общее число испытаний (бросаний n костей); 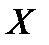– число появлений интересующего нас события (на m костях из n появится по шестерке) в N испытаниях; 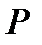– вероятность появления рассматриваемого события в одном испытании. Эту вероятность вычислим по формуле Бернулли

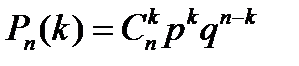
здесь число независимых испытаний n – это число брошенных костей, 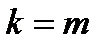, вероятность появления одного очка на грани одной кости 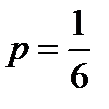, следовательно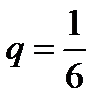

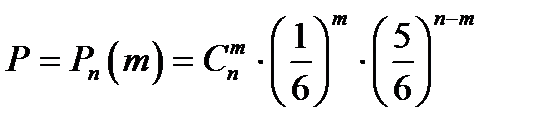
Итак, получим: