Проверка гипотезы о виде распределения
Пусть 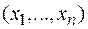 - выборка объема
- выборка объема 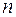 , представляющая собой результат
, представляющая собой результат 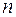 независимых наблюдений над случайной величиной
независимых наблюдений над случайной величиной 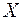 , относительно распределения которой выдвинута простая гипотеза
, относительно распределения которой выдвинута простая гипотеза 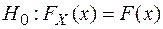
( 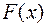 - теоретическая функция распределения, соответствующая гипотезе
- теоретическая функция распределения, соответствующая гипотезе 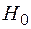 ). Наиболее распространенным критерием проверки этой гипотезы
). Наиболее распространенным критерием проверки этой гипотезы 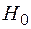 является критерии
является критерии 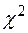 Пирсона.
Пирсона.
Чтобы воспользоваться критерием 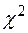 Пирсона, выборочные данные
Пирсона, выборочные данные 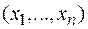 следует предварительно сгруппировать, представив их в виде интервального статистического ряда. Пусть
следует предварительно сгруппировать, представив их в виде интервального статистического ряда. Пусть 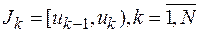 -интервалы группировки;
-интервалы группировки; 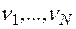 - частоты попадания выборочных значений в интервалы
- частоты попадания выборочных значений в интервалы 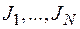 соответственно (
соответственно ( 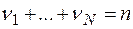 ).
).
Обозначим 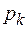 теоретическую (соответствующую
теоретическую (соответствующую 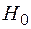 ) вероятность попадания случайной величины
) вероятность попадания случайной величины 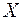 в интервал
в интервал 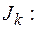
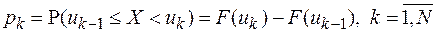 .
.
Статистикой критерия 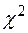 является величина:
является величина:

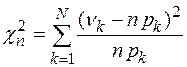 ,
,
которая характеризует отклонение эмпирической функции распределения 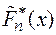 от теоретической функции распределения
от теоретической функции распределения 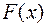 (значение
(значение 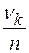 является приращением эмпирической функции
является приращением эмпирической функции 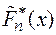 на интервале
на интервале 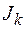 , а
, а 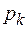 - приращением теоретической функции
- приращением теоретической функции 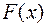 на том же интервале). Поскольку относительные частоты
на том же интервале). Поскольку относительные частоты 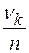 сближаются с вероятностями
сближаются с вероятностями 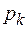 при
при 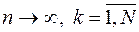 , то в случае справедливости гипотезы
, то в случае справедливости гипотезы 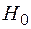 значение величины
значение величины 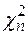 не должно существенно отличаться от нуля. Поэтому критическая область критерия
не должно существенно отличаться от нуля. Поэтому критическая область критерия 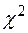 задается в виде
задается в виде 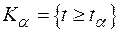 , где
, где 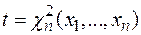 – значение величины
– значение величины 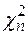 , полученное для заданной выборки, а порог
, полученное для заданной выборки, а порог 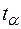 определяется по заданному уровню значимости
определяется по заданному уровню значимости 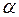 так, чтобы
так, чтобы 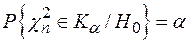 . Нахождение
. Нахождение 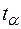 основано на том факте (известном как теорема Пирсона), что случайная величина
основано на том факте (известном как теорема Пирсона), что случайная величина 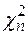 имеет при
имеет при 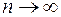 предельное распределение хи - квадрат
предельное распределение хи - квадрат 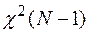 с
с 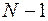 степенью свободы.
степенью свободы.
На практике предельное распределение 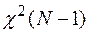 можно использовать с хорошим приближением при
можно использовать с хорошим приближением при 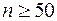 и
и 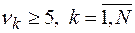 . При выполнении этих условий для заданного уровня значимости
. При выполнении этих условий для заданного уровня значимости 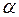 можно положить
можно положить 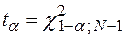 , где
, где 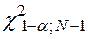 является (1—
является (1— 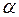 )-квантилью распределения
)-квантилью распределения 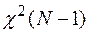 .
.
Таким образом, критерий согласия 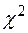 Пирсона состоит в следующем:
Пирсона состоит в следующем:
1. По заданному уровню значимости 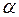 находится по табл. П4 порог
находится по табл. П4 порог
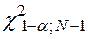 .
.
2. По заданной выборке 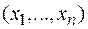 объема
объема 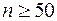 определяется число
определяется число 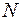 интервалов группировки так, чтобы
интервалов группировки так, чтобы 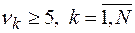 . Вычисляется значение статистики
. Вычисляется значение статистики 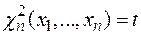 .
.
3. Если 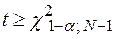 , то гипотезу
, то гипотезу 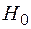 отвергают.
отвергают.
4. Если 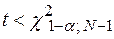 , то гипотезу
, то гипотезу 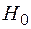 принимают.
принимают.
Если случайная величина 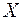 дискретная,
дискретная, 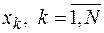 - различные выборочные значения, а
- различные выборочные значения, а 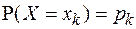 в случае справедливости
в случае справедливости 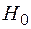 , то всегда можно определить
, то всегда можно определить 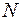 интервалов, содержащих ровно по одному выборочному значению. Поэтому в данном случае можно сразу считать, что
интервалов, содержащих ровно по одному выборочному значению. Поэтому в данном случае можно сразу считать, что 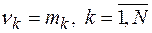 , где
, где 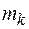 – частота выборочного значения
– частота выборочного значения 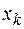 .
.
На практике теоретическое распределение полностью бывает определено редко. Чаще известен предположительно только тип распределения, но неизвестны параметры его определяющие. В этом случае гипотеза о виде распределения, подлежащая проверке, имеет вид 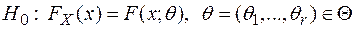 и является сложной параметрической гипотезой.
и является сложной параметрической гипотезой.
Критерий согласия 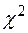 Пирсона применим для проверки такой гипотезы
Пирсона применим для проверки такой гипотезы 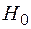 со следующими изменениями:
со следующими изменениями:
а) вероятности 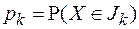 ,
, 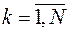 вычисляют, заменяя неизвестные параметры
вычисляют, заменяя неизвестные параметры 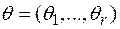 их оценками максимального правдоподобия
их оценками максимального правдоподобия 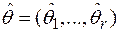 :
: 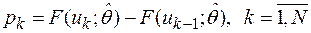 ;
;
б) число степеней свободы предельного распределения хи - квадрат должно быть уменьшено на число неизвестных параметров и считаться равным 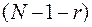 .
.
