Классический метод анализа переходных процессов

Введение

Основными задачами РГР являются:

1. самостоятельный анализ переходных процессов в линейных электрических цепях;

2. расчет электрических цепей с одним и двумя энергоемкими элементами классическим и операторным методами;

3. определение переходной и импульсной характеристик линейных цепей;

4. нахождение реакции цепи на произвольное внешнее воздействие по ее переходной и импульсной характеристикам.

КЛАССИЧЕСКИЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ

Задание:

1.1.Провести анализ переходного процесса в цепи с одним энергоемким элементом, схема которой представлена на (рис. 1), значения параметров в (табл. 1)

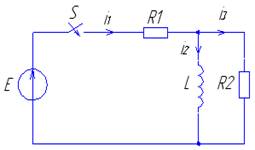
Рис. 1

Таблица 1

Величины параметров элементов цепи	Искомый ток
E, B	L, мГн	R1, Ом	R2, Ом
				i2(t)

1.1.1.Определить заданный ток и напряжения на элементах цепи в переходном режиме.

Решение:

Рассмотрим переходный процесс при замыкании ключа в цепи (рис. 1) с одним энергоемким элементом, используя классический метод анализа.

Анализ цепи до коммутации показывает, что ток индуктивности

i₂(0-) =0.

Независимое начальное условие определяется на основании первого закона коммутации и может быть зависимо:

,

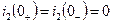т.е. ток индуктивности в первый момент после коммутации равен току индуктивности до коммутации, а затем может плавно изменяться.

Для нахождения заданного тока i₂(t) составим дифференциальное уравнение цепи после коммутации. Дифференциальное уравнение цепи получим из системы уравнений электрического равновесия цепи

i₁ = i₂ + i₃; U_R1 = i₁R₁; (1)

U_R1 + U_L = E; U_R2 = i₃ R_2;

U_R2 - U_L = 0;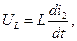

последовательно исключая все неизвестные величины кроме тока i₂, запишем выражение

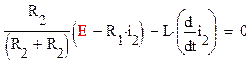(2)

Используя свойства дифференциала приходим к дифференциальному уравнению цепи

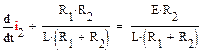(3)

Решение уравнения (3) будем искать в виде суммы свободной i_2св и вынужденной i_2вын составляющих тока второй ветви

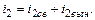(4)

Свободную составляющую тока 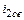находим, решая однородное дифференциальное уравнение, полученное из дифференциального уравнения цепи (3) (правая часть равна нулю)

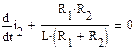
(5)

Далее составляем характеристическое уравнение цепи

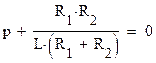
находим его корень

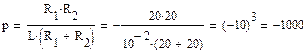
и определяем вид свободной составляющей тока второй ветви

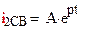
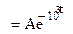
Анализ установившегося процесса в цепи после коммутации позволяет найти вынужденную составляющую тока 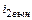(частное решение дифференциального уравнения цепи)

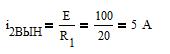
Общий вид реакции цепи соответствует сумме вынужденной и свободной составляющих тока второй ветви

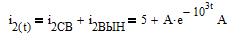
Определим постоянную интегрирования А по зависимым начальным условиям, т.е. по значению тока 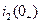в начальный момент времени после коммутации t=0₊

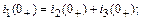
Т.к. 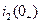=0, то отсюда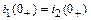

Тогда постоянная интегрирования при подстановки 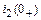будет равна А=-5

Таким образом ток 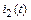после замыкания ключа будет записан в виде

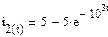
Напряжения на резисторах R₁ и R₂ можно определить, используя компонентное уравнение

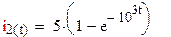A

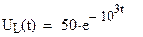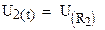
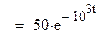В

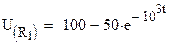В

В

1.1.2. Построим график тока второй ветви 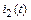цепи, рассмотренной в задании 1.1.1.

Данный график (рис. 2) построим при помощи программы Mathcad 15 Portable.

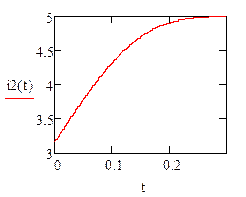Рис. 2

1.2.Методика анализа переходного процесса классическим методом в цепи с двумя энергоемкими элементами.

Проведем анализ переходного процесса в цепи (рис. 3) при замыкании ключа S. Величины параметров элементов и искомая реакция цепи приведены в (табл. 2).

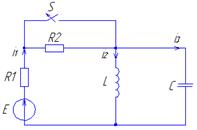
Рис. 3

Таблица 2

Величины параметров элементов цепи	Искомый ток
E, B	R1, Ом	R2, Ом	C, пФ	L,мкГн	i1(t)

Анализ цепи до коммутации показывает, что ток через катушку индуктивности 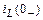равен нулю, также равно нулю напряжение на конденсаторе .

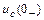Независимые начальные условия на основании законов коммутации:

,

.

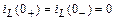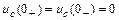Составим дифференциальное уравнение цепи после коммутации. Для этого запишем систему уравнений электрического равновесия цепи (рис. 3) относительно неизвестных токов и напряжений ее ветвей:

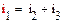(5)

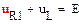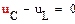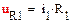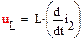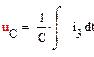Из полученной системы уравнений (5) исключим все неизвестные кроме одной переменной i₁

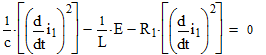
(6)

Чтобы избавиться от интегралов в последнем уравнении, осуществим дифференцирование его по времени. Преобразуя, получим

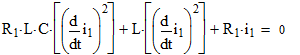(7)

Решение уравнения (7) найдем как сумму свободной i_1св и вынужденной i_1вын составляющих тока второй ветви.

i₁= i_1св+ i_1вын.

Анализ установившегося процесса после коммутации связан с частным решением дифференциального уравнения цепи (6) и проводится по результатам анализа цепи в установившемся режиме при .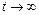

Вынужденная составляющая тока второй ветви будет равна:

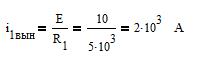
Свободную составляющую тока 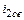находим, составляя характеристическое уравнение цепи, решая однородное дифференциальное уравнение цепи:

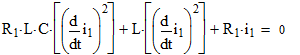(7)

Находим его корни

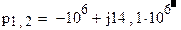с^-1

Таким образом, свободная составляющая тока второй ветви будет равна:

.

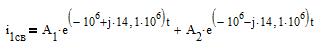Общий вид реакции цепи в переходном режиме равен сумме вынужденной и свободной составляющих тока второй ветви

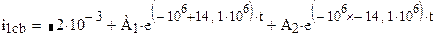(8)

Определим постоянные интегрирования. В данном случае их две 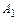и 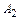для их нахождения необходимо два уравнения. Первое получим из выражения для тока второй ветви в первый момент после коммутации (при )

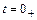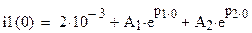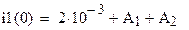или . (9)

Второе уравнение получим, определив производную от уравнения тока второй ветви

,

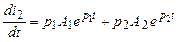в начальный момент после коммутации

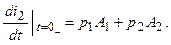(10)

Однако в уравнениях кроме постоянных интегрирования неизвестны и зависимые начальные условия 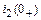и 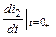, которые необходимо определить из независимых начальных условий и уравнений электрического равновесия цепи в начальный момент после коммутации

;

;

.

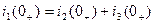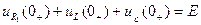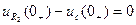На основании законов коммутаци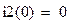и и 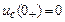, тогда

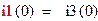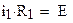Находим постоянные интегрирования

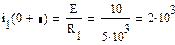А₁=-А₂

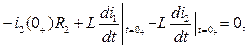
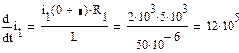
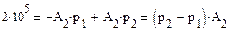
ж

А₂ =j0,71 A

Определим реакцию цепи, т.е. ток второй ветви после коммутации. Подставив постоянные интегрирования в уравнение

Выражение тока второй ветви с учетом соотношения

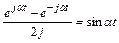
может быть преобразовано к виду 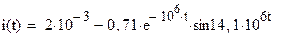А.

1.2.2. Построим график функции тока второй ветви, используя программу MathCad 15 Portable. (рис. 6)

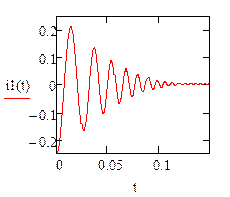
Рис. 4

Как видно из (рис. 4) колебательный процесс носит затухающий характер.