Операторный метод анализа переходных колебаний в Электрических Цепях
Классический метод анализа переходных колебаний в Электрических Цепях
При выполнении задачи анализа переходных колебаний в ЭЦ классическим методом рекомендуется следующая последовательность действий:
• рассчитываются начальные условия задачи;
• составляется система уравнений с использованием законов Кирхгофа;
• выбирается переменная uC или iL,формируется дифференциальное уравнение с этой переменной соответствующего порядка и записывается его решение;
• рассчитывается вынужденная составляющая (при t ® ¥) для выбранной переменной;
• рассчитывается свободная составляющая для выбранной переменной.
1.1. Анализ переходных колебаний в разветвленных RC-цепях
путем составления дифференциального уравнения
[1, с. 185–187; 2, с. 157–167]
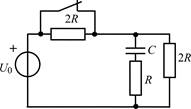 |
| Рис. 1.1 |
1.1.0. Найдите законы изменения напряжения uC(t) на емкости и тока iC(t) через емкость в цепи на рис. 1.1 после размыкания ключа. Постройте примерные графики.
Во всех задачах анализа переходных колебаний предполагается, что до коммутации в цепи был установившийся режим, и положение ключа на схеме цепи показано до коммутации.
В задачах 1.1.1–1.1.25 найдите законы изменения напряжения uC(t) на емкости и тока iC(t) через емкость после коммутации. Постройте примерные графики.
Таблица 1.1
| Вариант | Схема RC-цепи | Вариант | Схема RC-цепи |
| 1.1.1 | 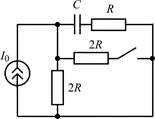 | 1.1.2 | 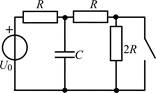 |
| 1.1.3 | 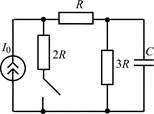 | 1.1.4 | 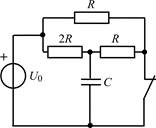 |
| 1.1.5 | 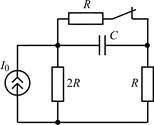 | 1.1.6 | 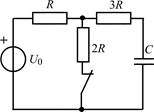 |
| 1.1.7 | 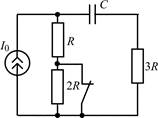 | 1.1.8 | 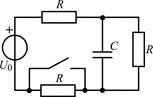 |
| 1.1.9 | 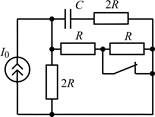 | 1.1.10 | 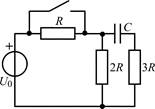 |
Продолжение табл. 1.1
| Вариант | Схема RC-цепи | Вариант | Схема RC-цепи |
| 1.1.11 | 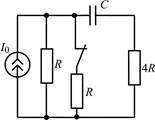 | 1.1.12 | 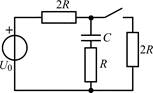 |
| 1.1.13 | 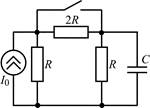 | 1.1.14 | 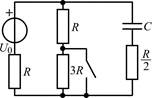 |
| 1.1.15 | 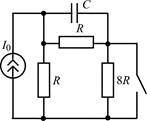 | 1.1.16 | 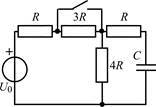 |
| 1.1.17 | 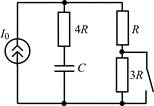 | 1.1.18 | 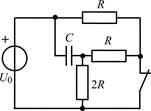 |
| 1.1.19 | 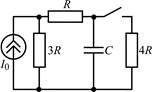 | 1.1.20 | 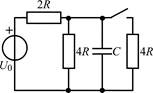 |
Окончание табл. 1.1
| Вариант | Схема RC-цепи | Вариант | Схема RC-цепи |
| 1.1.21 | 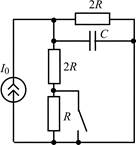 | 1.1.22 | 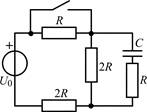 |
| 1.1.23 | 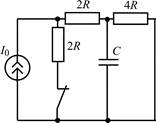 | 1.1.24 | 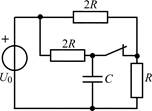 |
| 1.1.25 | 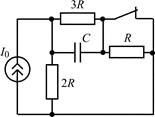 |
1.2. Анализ переходных колебаний в разветвленных RL-цепях
путем составления дифференциального уравнения
[1, с. 185–197; 2, с. 157–167]
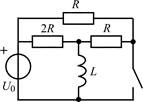 |
| Рис. 1.2 |
1.2.0. Найдите закон изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности в цепи на рис. 1.2 после замыкания ключа. Постройте примерные графики.
В задачах 1.2.1–1.2.25 найдите законы изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Таблица 1.2
| Вариант | Схема RL-цепи | Вариант | Схема RL-цепи |
| 1.2.1 | 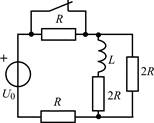 | 1.2.2 | 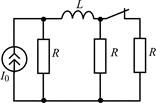 |
| 1.2.3 | 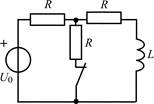 | 1.2.4 | 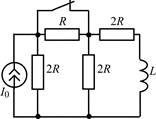 |
| 1.2.5 | 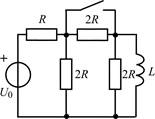 | 1.2.6 | 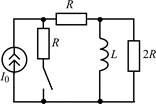 |
| 1.2.7 | 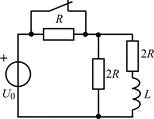 | 1.2.8 | 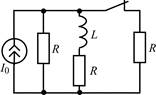 |
Продолжение табл. 1.2
| Вариант | Схема RL-цепи | Вариант | Схема RL-цепи | |
| 1.2.9 | 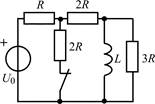 | 1.2.10 | 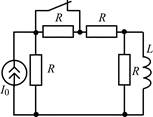 | |
| 1.2.11 | 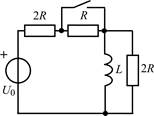 | 1.2.12 | 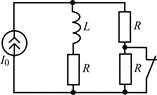 | |
| 1.2.13 | 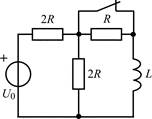 | 1.2.14 | 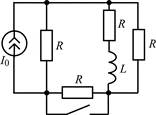 | |
| 1.2.15 | 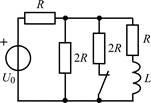 | 1.2.16 | 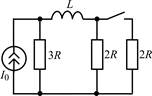 | |
| 1.2.17 | 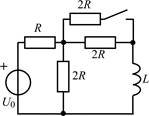 | 1.2.18 | 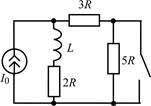 | |
Окончание табл. 1.2
| Вариант | Схема RL-цепи | Вариант | Схема RL-цепи |
| 1.2.19 | 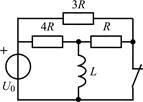 | 1.2.20 | 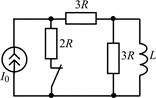 |
| 1.2.21 | 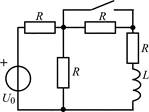 | 1.2.22 | 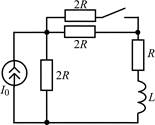 |
| 1.2.23 | 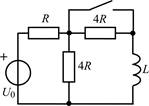 | 1.2.24 | 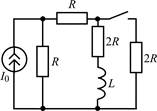 |
| 1.2.25 | 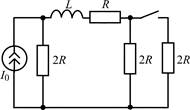 |
1.3. Анализ разветвленной цепи с одним реактивным элементом
с использованием формулы 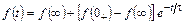
[1, с. 197–198]
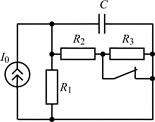 |
| Рис. 1.3 |
1.3.0. Найдите законы изменения напряжения uC(t) на емкости и тока iС(t) через емкость в цепи на рис. 1.3 после размыкания ключа, если I0 = 1 А; R1 = R2 = 36 Ом; R3 = 144 Ом; С = 0,1 мкФ. Постройте примерные графики.
В задачах 1.3.1–1.3.25 в RC-цепяхнайдите законы изменения напряжения uС(t) на емкости и тока iС(t) через емкость, в RL-цепях найдите законы изменениятока iL(t) в индуктивности и напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Таблица 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.1 | 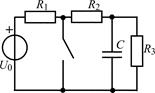 U0 = 25 В; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 0,5 мкФ U0 = 25 В; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 0,5 мкФ | 1.3.2 | 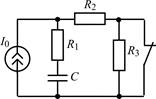 I0 = 5 мА; R1 = 2 кОм; R2 = 3 кОм; R3 = 5 кОм; С = 0,1 мкФ I0 = 5 мА; R1 = 2 кОм; R2 = 3 кОм; R3 = 5 кОм; С = 0,1 мкФ |
| 1.3.3 | 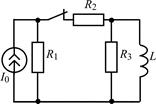 I0 = 8 мА; R1 = R2 = 5 кОм; R3 = 4 кОм; L = 0,8 Гн I0 = 8 мА; R1 = R2 = 5 кОм; R3 = 4 кОм; L = 0,8 Гн | 1.3.4 | 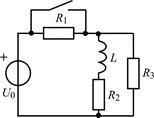 U0 = 40 В; R1 = 15 кОм; R2 = R3 = 10 кОм; L = 0,5 Гн U0 = 40 В; R1 = 15 кОм; R2 = R3 = 10 кОм; L = 0,5 Гн |
Продолжение табл. 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.5 | 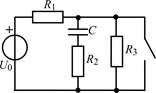 U0 = 10 В; R1 = 2 кОм; R2 = 4 кОм; R3 = 8 кОм; С = 0,25 мкФ U0 = 10 В; R1 = 2 кОм; R2 = 4 кОм; R3 = 8 кОм; С = 0,25 мкФ | 1.3.6 | 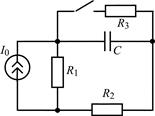 I0 = 5 мА; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 5000 пФ I0 = 5 мА; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 5000 пФ |
| 1.3.7 | 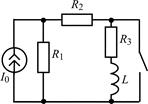 I0 = 10 мА; R1 = R3 = 1 кОм; R2 = 3 кОм; L = 20 мГн I0 = 10 мА; R1 = R3 = 1 кОм; R2 = 3 кОм; L = 20 мГн | 1.3.8 | 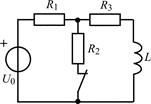 U0 = 12 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 12 мГн U0 = 12 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 12 мГн |
| 1.3.9 | 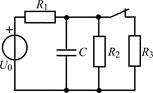 U0 = 60 В; R1 = 4 кОм; R2 = R3 = 2 кОм; С = 0,3 мкФ U0 = 60 В; R1 = 4 кОм; R2 = R3 = 2 кОм; С = 0,3 мкФ | 1.3.10 | 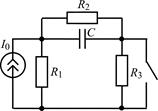 I0 = 8 мА;R1 = R2 = 10 кОм; R3 = 20 кОм; С = 0,2 мкФ I0 = 8 мА;R1 = R2 = 10 кОм; R3 = 20 кОм; С = 0,2 мкФ |
| 1.3.11 | 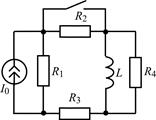 I0 = 15 мА; R1 = 100 Ом; R2 = R3 = 200 Ом; R4 = 300 Ом; L = 0,15 Гн I0 = 15 мА; R1 = 100 Ом; R2 = R3 = 200 Ом; R4 = 300 Ом; L = 0,15 Гн | 1.3.12 | 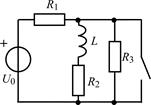 U0 = 20 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 4 мГн U0 = 20 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 4 мГн |
Продолжение табл. 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.13 | 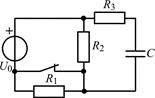 U0 = 24 В; R1 = R2 = 4 кОм; R3 = 3 кОм; С = 0,2 мкФ U0 = 24 В; R1 = R2 = 4 кОм; R3 = 3 кОм; С = 0,2 мкФ | 1.3.14 | 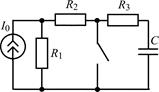 I0 = 4 мА; R1 = 5 кОм; R2 = 3 кОм; R3 = 2 кОм; С = 0,5 мкФ I0 = 4 мА; R1 = 5 кОм; R2 = 3 кОм; R3 = 2 кОм; С = 0,5 мкФ |
| 1.3.15 | 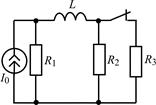 I0 = 6 мА; R1 = R2 = R3 = 2 кОм; L = 40 мГн I0 = 6 мА; R1 = R2 = R3 = 2 кОм; L = 40 мГн | 1.3.16 | 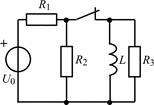 U0 = 30 В; R1 = 2 кОм; R2 = R3 = 6 кОм; L = 6 мГн U0 = 30 В; R1 = 2 кОм; R2 = R3 = 6 кОм; L = 6 мГн |
| 1.3.17 | 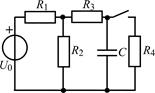 U0 = 36 В; R1 = R2 = R4 = 2 кОм; R3 = 1 кОм; С = 0,5 мкФ U0 = 36 В; R1 = R2 = R4 = 2 кОм; R3 = 1 кОм; С = 0,5 мкФ | 1.3.18 | 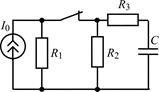 I0 = 10 мА; R1 = R2 = 2 кОм; R3 = 3 кОм; С = 0,4 мкФ I0 = 10 мА; R1 = R2 = 2 кОм; R3 = 3 кОм; С = 0,4 мкФ |
| 1.3.19 | 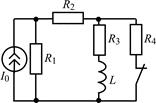 I0 = 20 мА; R2 = 1 кОм; R1 = R3 = R4 = 2 кОм; L = 50 мГн I0 = 20 мА; R2 = 1 кОм; R1 = R3 = R4 = 2 кОм; L = 50 мГн | 1.3.20 | 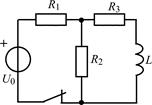 U0 = 40 В; R1 = 240 Ом; R2 = 800 Ом; R3 = 200 Ом; L = 0,2 Гн U0 = 40 В; R1 = 240 Ом; R2 = 800 Ом; R3 = 200 Ом; L = 0,2 Гн |
Окончание табл. 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.21 | 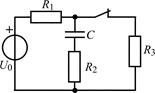 U0 = 24 В;R1 = 2 кОм; R2 = 3 кОм; R3 = 4 кОм; С = 0,2 мкФ U0 = 24 В;R1 = 2 кОм; R2 = 3 кОм; R3 = 4 кОм; С = 0,2 мкФ | 1.3.22 | 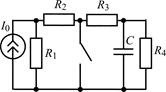 I0 = 20 мА; R1 = 3 кОм; R2 = R3 = R4 = 1 кОм; С = 0,2 мкФ I0 = 20 мА; R1 = 3 кОм; R2 = R3 = R4 = 1 кОм; С = 0,2 мкФ |
| 1.3.23 | 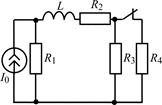 I0 = 36 мА; R1 = 4 кОм; R2 = 3 кОм; R3 = R4 = 2 кОм; L = 18 мГн I0 = 36 мА; R1 = 4 кОм; R2 = 3 кОм; R3 = R4 = 2 кОм; L = 18 мГн | 1.3.24 | 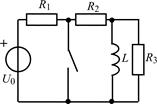 U0 = 25 В; R1 = 300 Ом; R2 = 200 Ом; R3 = 800 Ом; L = 0,16 Гн U0 = 25 В; R1 = 300 Ом; R2 = 200 Ом; R3 = 800 Ом; L = 0,16 Гн |
| 1.3.25 | 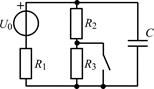 | U0 = 6 В; R1 = R2 = 2 кОм; R3 = 8 кОм; С = 0,5 мкФ |
1.4. Анализ свободных (переходных) колебаний
при отключении (подключении) к цепи
источника гармонических колебаний
[1, с. 185–198; 2, с. 157–167]
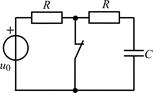 |
| Рис. 1.4 |
1.4.0. Найдите закон изменения напряжения uC(t) на емкости в цепи на рис. 1.4 после размыкания ключа, если u0(t) = 5cos106t В, R = 500 Ом, С = 1000 пФ. Постройте примерный график.
В задачах 1.4.1–1.4.6 найдите закон изменения тока iL(t) в индуктивности после коммутации. Постройте примерные графики.
Таблица 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.1 | 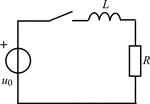 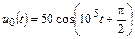 , В; R = 5 кОм; L = 50 мГн , В; R = 5 кОм; L = 50 мГн | 1.4.2 | 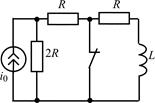 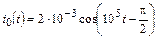 , А; R = 1 кОм; L = 40 мГн , А; R = 1 кОм; L = 40 мГн |
| 1.4.3 | 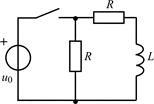 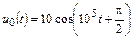 , В; R = 2 кОм; L = 20 мГн , В; R = 2 кОм; L = 20 мГн | 1.4.4 | 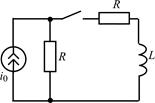 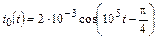 , А; R = 0,5 кОм; L = 10 мГн , А; R = 0,5 кОм; L = 10 мГн |
| 1.4.5 | 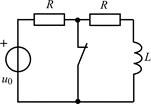 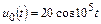 , В; R = 1 кОм; L = 20 мГн , В; R = 1 кОм; L = 20 мГн | 1.4.6 | 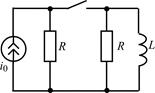 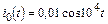 , А; R = 0,3 кОм; L = 15 мГн , А; R = 0,3 кОм; L = 15 мГн |
В задачах 1.4.7–1.4.13 найдите закон изменения напряжения uC(t) на емкости после коммутации. Постройте примерные графики.
Продолжение табл. 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.7 | 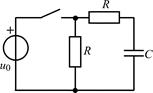 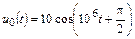 , В; R = 2 кОм; C = 500 пФ , В; R = 2 кОм; C = 500 пФ | 1.4.8 | 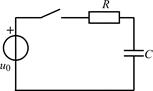 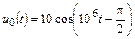 , В; R = 1 кОм; C = 1000 пФ , В; R = 1 кОм; C = 1000 пФ |
| 1.4.9 | 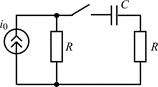 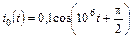 , А; R = 40 Ом; С = 0,0125 мкФ , А; R = 40 Ом; С = 0,0125 мкФ | 1.4.10 | 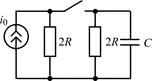 i0 = 0,05cos107t, А; R = 1 кОм; C = 100 пФ i0 = 0,05cos107t, А; R = 1 кОм; C = 100 пФ |
| 1.4.11 | 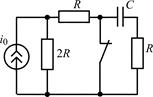 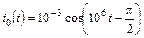 , А; R = 500 Ом; С = 500 пФ , А; R = 500 Ом; С = 500 пФ | 1.4.12 | 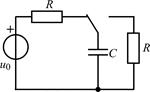 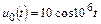 , В; R = 1 кОм; C = 1000 пФ , В; R = 1 кОм; C = 1000 пФ |
| 1.4.13 | 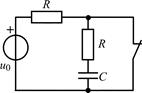 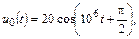 В; R = 500 Ом; C = 1000 пФ В; R = 500 Ом; C = 1000 пФ |
В задачах 1.4.14–1.4.19 найдите закон изменения напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Продолжение табл. 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.14 | 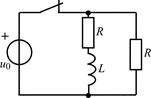 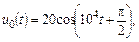 В; R = 500 Ом; L = 50 мГн В; R = 500 Ом; L = 50 мГн | 1.4.15 | 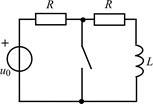 u0(t) = 20cos105t В; R = 500 Ом; L = 10 мГн u0(t) = 20cos105t В; R = 500 Ом; L = 10 мГн |
| 1.4.16 | 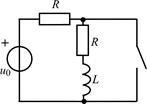 u0(t) = 10cos105t , В; R = 1 кОм; L = 20 мГн u0(t) = 10cos105t , В; R = 1 кОм; L = 20 мГн | 1.4.17 | 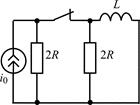 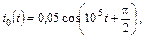 А; R = 5 кОм; L = 50 мГн А; R = 5 кОм; L = 50 мГн |
| 1.4.18 | 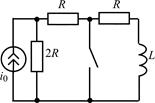 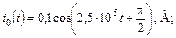 R = 2,5 кОм; L = 40 мГн R = 2,5 кОм; L = 40 мГн | 1.4.19 | 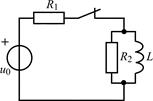 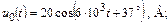 R1 = 10 Ом; R2 = 60 Ом; L = 10 мГн R1 = 10 Ом; R2 = 60 Ом; L = 10 мГн |
В задачах 1.4.20–1.4.25 найдите закон изменения тока iC(t) через емкость после коммутации. Постройте примерные графики.
Окончание табл. 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.20 | 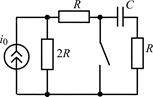 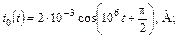 R = 1 кОм; С = 250 пФ R = 1 кОм; С = 250 пФ | 1.4.21 | 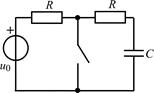 u0 = 8cos106t , В; R = 2 кОм; С = 250 пФ u0 = 8cos106t , В; R = 2 кОм; С = 250 пФ |
| 1.4.22 | 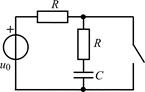 u0(t) = 20cos107t, В; R = 200 Ом; С = 250 пФ u0(t) = 20cos107t, В; R = 200 Ом; С = 250 пФ | 1.4.23 | 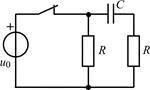 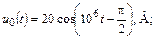 R = 2 кОм; С = 500 пФ R = 2 кОм; С = 500 пФ |
| 1.4.24 | 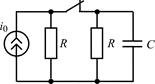 i0(t) = 0,01cos4×104t , А; R = 10 кОм; С = 5000 пФ i0(t) = 0,01cos4×104t , А; R = 10 кОм; С = 5000 пФ | 1.4.25 | 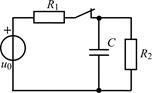 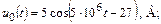 R1 = 0,5 кОм; R2 = 1 кОм; С = 2000 пФ R1 = 0,5 кОм; R2 = 1 кОм; С = 2000 пФ |
1.5. Составление уравнений переменных состояния цепи
[1, с. 89–93, 211–218; 2, с. 178–183]
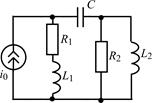 |
| Рис. 1.5 |
1.5.0. Составьте систему линейных дифференциальных уравнений по методу переменных состояния в нормальной форме для цепи на рис. 1.5, используя законы Кирхгофа. Запишите полученную систему уравнений состояния цепи в матричной форме.
В задачах 1.5.1–1.5.25 составьте систему линейных дифференциальных уравнений по методу переменных состояния в нормальной форме, используя законы Кирхгофа. Запишите полученную систему уравнений состояния цепи в матричной форме.
Таблица 1.5
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.5.1 | 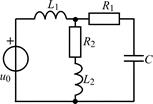 | 1.5.2 | 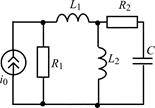 |
| 1.5.3 | 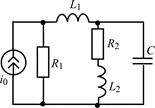 | 1.5.4 | 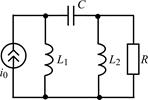 |
| 1.5.5 | 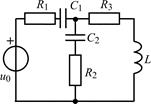 | 1.5.6 | 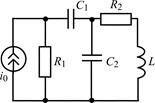 |
Продолжение табл. 1.5
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.5.7 | 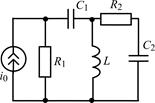 | 1.5.8 | 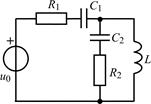 |
| 1.5.9 | 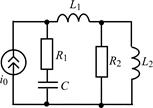 | 1.5.10 | 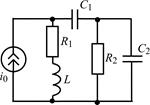 |
| 1.5.11 | 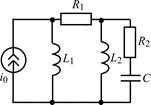 | 1.5.12 | 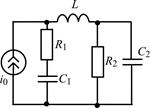 |
| 1.5.13 | 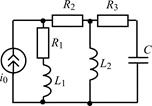 | 1.5.14 | 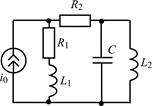 |
| 1.5.15 | 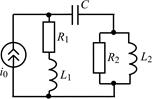 | 1.5.16 | 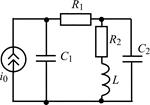 |
Окончание табл. 1.5
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.5.17 | 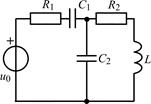 | 1.5.18 | 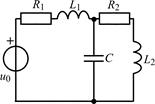 |
| 1.5.19 | 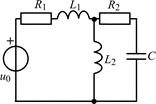 | 1.5.20 | 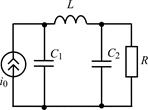 |
| 1.5.21 | 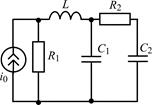 | 1.5.22 | 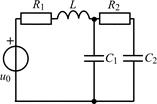 |
| 1.5.23 | 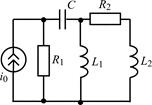 | 1.5.24 | 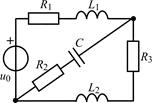 |
| 1.5.25 | 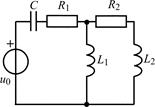 |
Контрольные вопросы
1. Что такое переходный процесс? В каких схемах он возникает и почему?
2. Что называют начальными условиями задачи?
3. Сформулируйте законы коммутации. Каков их физический смысл? Как они были использованы при решении задач?
4. От чего зависит порядок дифференциального уравнения цепи?
5. Когда режим в цепи называется свободным, когда вынужденным?
6. Чем отличаются дифференциальные уравнения, описывающие свободные и переходные колебания в цепи? Чем отличаются их решения?
7. Как находится характеристическое уравнение цепи по заданному дифференциальному уравнению?
8. Что называют постоянной времени цепи? Как от нее зависит длительность переходного процесса?
9. Как определяются постоянные времени RC- и RL-цепей?
10. Как определяются и от чего зависят собственные (свободные) колебания в цепи?
11. Как определяются и от чего зависят вынужденные колебания в цепи?
12. Что называют переменными состояния цепи?
13. Как составляются уравнения состояния цепи? Чем определяется порядок системы уравнений состояния цепи?
14. Запишите уравнения переменных состояния цепи в нормальной форме.
Операторный метод анализа переходных колебаний в Электрических Цепях
При выполнении задачи анализа переходных колебаний в ЭЦ операторным методом рекомендуется следующая последовательность действий:
• рассчитываются начальные условия задачи;
• составляется операторная схема замещения цепи, в которой ненулевые начальные условия учитываются введением дополнительных источников (рис. П2.1);
• определяется L-изображение искомого тока или напряжения любым из ранее изученных методов расчета цепей: методом эквивалентных преобразований, методом узловых напряжений, методом эквивалентного генератора;
• определяется мгновенное значение искомого тока или напряжения по таблице соответствия функций времени и их изображений (табл. П2.1) или по теореме разложения.
2.1. Анализ переходных колебаний в RC- и RL-цепях
при нулевых начальных условиях
[1, с. 218–243; 2, с. 185–196]
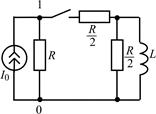 |
| Рис. 2.1 |
2.1.0. Найдите закон изменения напряжения u10(t) на зажимах генератора в цепи на рис. 2.1 после замыкания ключа. Постройте примерный график.
В задачах 2.1.1–2.1.4 найдите закон изменения напряжения uC(t) на емкости после коммутации. Постройте примерные графики.
Таблица 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.1 | 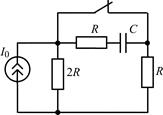 | 2.1.2 | 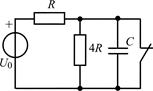 |
| 2.1.3 | 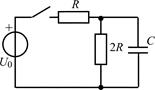 | 2.1.4 | 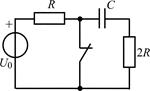 |
В задачах 2.1.5–2.1.10 найдите закон изменения тока iC(t) через емкость после коммутации. Постройте примерные графики.
Продолжение табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.5 | 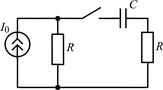 | 2.1.6 | 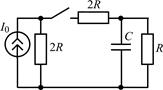 |
| 2.1.7 | 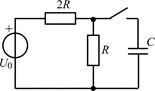 | 2.1.8 | 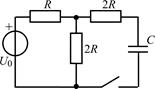 |
| 2.1.9 | 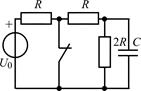 | 2.1.10 | 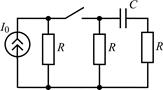 |
В задачах 2.1.11–2.1.16 найдите закон изменения тока iL(t) в индуктивности после коммутации. Постройте примерные графики.
Продолжение табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.11 | 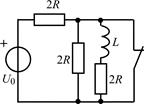 | 2.1.12 | 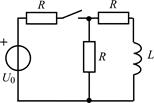 |
| 2.1.13 | 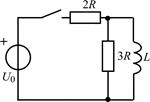 | 2.1.14 | 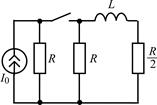 |
| 2.1.15 | 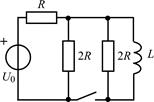 | 2.1.16 | 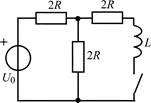 |
В задачах 2.1.17–2.1.22 найдите закон изменения напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Продолжение табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.17 | 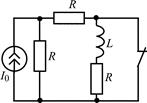 | 2.1.18 | 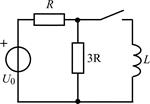 |
| 2.1.19 | 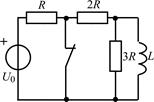 | 2.1.20 | 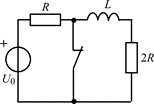 |
| 2.1.21 | 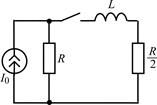 | 2.1.22 | 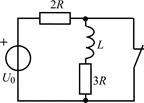 |
В задачах 2.1.23–2.1.25 найдите закон изменения тока i(t) после коммутации. Постройте примерные графики.
Окончание табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.23 | 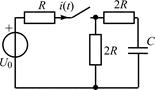 | 2.1.24 | 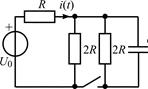 |
| 2.1.25 | 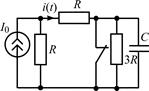 |
2.2. Анализ переходных колебаний в RC-цепях
при ненулевых начальных условиях
[1, с. 218–243; 2, с. 185–196]
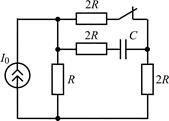 |
| Рис. 2.2 |
2.2.0. Найдите законы изменения напряжения uC(t) на емкости и тока iС(t) через емкость в цепи на рис. 2.2 после размыкания ключа. Постройте примерные графики.
В задачах 2.2.1–2.2.25 найдите законы изменения напряжения uC(t) на емкости и тока iС(t) через емкость после коммутации. Постройте примерные графики.
Таблица 2.2
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.2.1 | 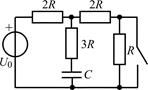 | 2.2.2 | 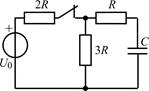 |
| 2.2.3 | 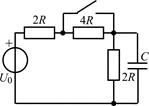 | 2.2.4 | 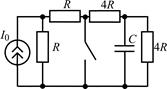 |
| 2.2.5 | 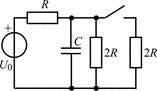 | 2.2.6 | 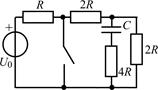 |
| 2.2.7 | 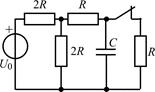 | 2.2.8 | 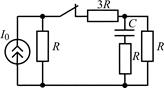 |
| 2.2.9 | 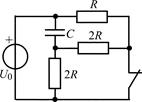 | 2.2.10 | 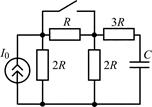 |
| 2.2.11 | 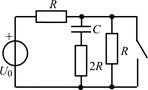 | 2.2.12 | 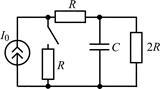 |
Продолжение табл. 2.2
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.2.13 | 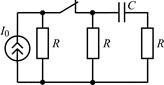 | 2.2.14 | 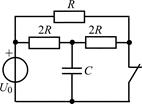 |
| 2.2.15 | 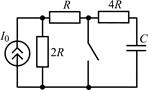 | 2.2.16 | 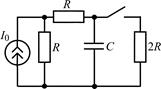 |
| 2.2.17 | 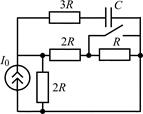 | 2.2.18 | 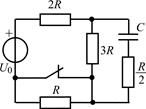 |
| 2.2.19 | 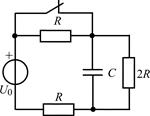 | 2.2.20 | 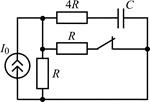 |
| 2.2.21 | 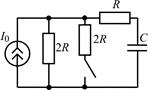 | 2.2.22 | 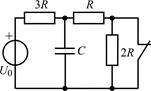 |
Окончание табл. 2.2
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.2.23 | 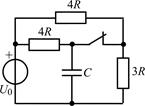 | 2.2.24 | 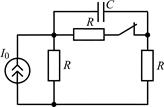 |
| 2.2.25 | 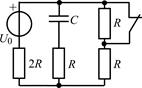 |
2.3. Анализ переходных колебаний в RL-цепях
при ненулевых начальных условиях
[1, с. 218–243; 2, с. 185–196]
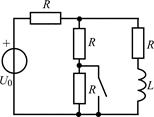 |
| Рис. 2.3 |
2.3.0. Найдите законы изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности в цепи на рис. 2.3 после замыкания ключа. Постройте примерные графики.
В задачах 2.3.1–2.3.25 найдите законы изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Таблица 2.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.3.1 | 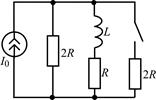 | 2.3.2 | 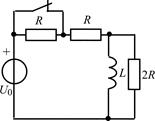 |
| 2.3.3 | 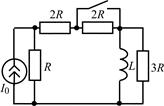 | 2.3.4 | 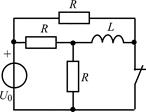 |
| 2.3.5 | 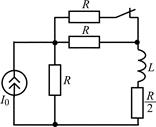 | 2.3.6 | 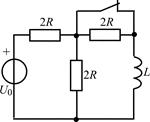 |
| 2.3.7 | 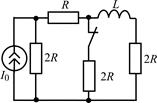 | 2.3.8 | 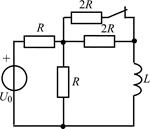 |
Продолжение табл.2.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.3.9 | 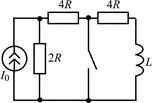 | 2.3.10 | 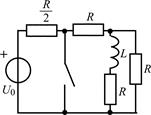 |
| 2.3.11 | 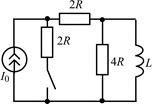 | 2.3.12 | 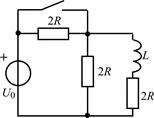 |
| 2.3.13 | 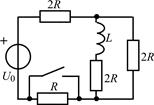 | 2.3.14 | 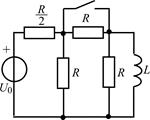 |
| 2.3.15 | 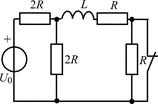 | 2.3.16 | 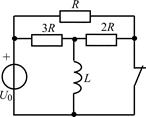 |
Окончание табл. 2.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.3.17 | 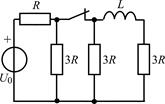 | 2.3.18 | 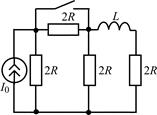 |
| 2.3.19 | 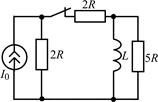 | 2.3.20 | 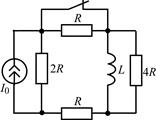 |
| 2.3.21 | 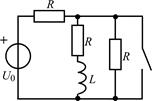 | 2.3.22 | 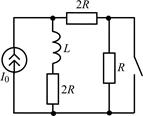 |
| 2.3.23 | 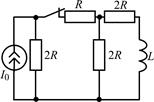 | 2.3.24 | 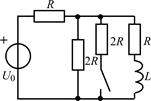 |
| 2.3.25 | 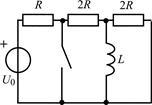 |
Контрольные вопросы
1. Какие функции преобразуемы по Лапласу?
2. Как связаны оригинал и изображение по Лапласу?
3. Сформулируйте основные свойства преобразования Лапласа.
4. Чему равны операторные сопротивления индуктивности, емкости, резистивного сопротивления?
5. Какие законы электрической цепи справедливы для L-изображений колебаний?
6. Как учитывается начальный запас энергии в индуктивности и емкости при составлении операторной схемы замещения цепи?
7. Нарисуйте операторные схемы замещения индуктивности и емкости при ненулевых начальных условиях.
8. Каков порядок анализа переходных колебаний в цепи операторным методом?
9. Сформулируйте теорему разложения.
10. Каков порядок нахождения оригинала по его L-изображению с помощью теоремы разложения?
11. Как по виду L-изображения реакции цепи найти ее постоянную времени t?
