Жоғарғы ретті туындылар мен дифференциалдар.

Анықтама. 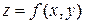функциясының ретті дербес туындысы деп оның ретті кезкелген туындысының дербес туындысын айтамыз.

Бұл рекуренттік анықтама функцияның ретті дербес туындысын бұл функцияның дербес туындыларын бірінің артынан бірін табу жолымен табу мүмкіндігін береді. функциясы нөлінші ретті туынды деп есептеледі. функциясының бірінші ретті және туындыларынан 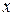, 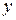бойынша туындылар алып төрт екінші ретті туындылар аламыз: , , , . Бұлардан 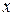, 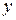бойынша тағы да туындылар алып 3-і ретті 8 дербес туындыларды табамыз. ретті екі айнымалының туындысы бар.

Мысал. - функциясының 1-і, 2-і ретті дербес туындыларын табайық.

, , , , , . Бұл мысалда және бұл кездейсоқ емес.

Анықтама. Функцияның әртүрлі айнымалыларымендифференциалдауы бар дербес туындысы аралас туынды деп аталады.

Екі айнымалы функциясының 2-і ретті аралас туындысы және болды.

Теорема (аралас туындылар туралы). 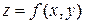функциясы және , , , туындылары нүктесінің кейбір аймағында үзіліссіз болсын. Онда бұл нүктеде оның аралас 2-і ретті туындылары өз ара тең болады: .

Дәлелдеуі.Мына

.өрнекті қарайық. Егер деп белгілеп оған Лагранж теоремасын қолдансақ, онда (тағы да Лагранж теоремасын үшін қолданайық)= . Мұнда және , егер болса. 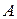-ны басқа түрде жазайық, деп белгілеп, Лагранж теоремасы көмегімен аламыз:

. Мұнда , . 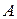-ның осы екі мәнін теңестіріп аламыз: =

Соңғы теңдеудің екі жағында -ге шекке ұмтылдырып, , үзіліссіздігін ескеріп табамыз: . Теорема дәледенді.

Салдар. нүктесінің маңайында функциясының –гедейінгі барлық дербес туындылары, барлық ретті аралас туындылары үзіліссіз болсын. Онда бұл нүктеде оның ретті барлық аралас туындылары, тек дифференциалдау реті өзгеше, өз ара тең болады. Бұл салдар 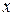бойынша , 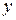бойынша дифференциалдары бар белгілеулер қолдануға болады: . Салдардың шарттары орындалғанда дифференциалдау реттері қортындыға әсер етпейді.

Мысал. болсын. табайық., . Кез келген дифференциалдау реті бойынша екі дифференциалдау кезінде қорытынды осындай болады.

Анықтама. нүктесінің маңайында ретке дейінгі барлық дербес туындылары бар және үзілісіз 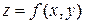функциясы осы нүктеде рет дифференциаданатын функция деп аталады.

Анықтама. 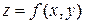де рет дифференциалданатын болсын. Осы функцияның ретті дифференциалы деп, , - тұрақты болып қалған жағдайда оның –і толық дифференциалынан алынған толық дифференциалын айтамыз . Ол түрінде белгіленеді. Мысалы,

. (1)

Осы сияқты 3-ретті толық дифференциалдау формуласын табуға болады.

. (2)

Осы толық дифференциалдар формулаларындағы дербес туындылар алдындағы коэффициенттер Ньютон биномындағы коэффициенттермен сәйкес келеді. функциясының -ін табу үшін формула жазайық:

Бұл толық дифференциалдар функциясын есептеу үшін қолданылады. Бұрын осы формуланы бірінші дифференциалдау көмегімен жуықтап есептеуге қолдандық:

. Толық дифференциалдардың жеткілікті санын алып берілген мәнді алдын – ала берілген дәлдіктен Тейлор формуласының көмегімен табуға болады:

. (4)

Мысал. функциясының -ін табайық..Барлық 2-ші ретті дербес туындыларын табайық: ; ;

; ; .

Бұл туындылары (1)-ге қойып аламыз:

. Егер , , болса, онда .

Әдебиеттер: 9 нег.[241-243], 11 нег. [314-320].

Бақылау сұрақтар:

1. Күрделі функцияның туындысы.

2. Айқындалмаған функцияның туындысы.

3. Жоғарғы ретті туындылар мен дифференциалдар.

4. Градиенттің қасиеттері.

5. Аралас туындылар туралы.

№15-дәріс. Екі айнымалы функцияның экстремумы.

1-анықтама. 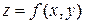функциясының максимум нүктесі деп аталады, егер осы нүктенің маңайдағы барлық үшін мына теңсіздік

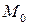орындалса. Егер маңайдағы барлық үшін мына теңсіздік орындаслса, онда нүктесі минимум нүктесі деп аталады.

Максимум нүктесіндегі функция мәні функциясыныңмаксимумы деп, ал минимум нүктесіндегі мәні -минимумы деп аталады.

Максимум және минимум нүктелері – функцияның экстремаль нүктелері деп аталады, ал максимумдер мен минимумдер - функцияның экстремумдері деп аталады. 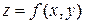функциясы 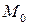нүктесінің кейбір аймағында анықталсын. Егер 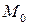нүктесінде , нольге тең болса, не анықталмаса, онда 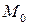нүктесі 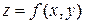функцияның күдікті (крезистік) нүктесі деп аталады. Келесі теорема бір айнымалы функцияның экстремумның қажетті шартына ұқсас.

Теорема 1 (экстремумның қажетті шарты).Егер 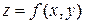функциясының экстремаль нүктесі болса, онда 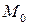осы функцияның күдікті нүктесі болады.

Дәлелдеуі.Бір айнымалы тің функциясын қарайық. Экстремаль нүктенің анықтамасынан 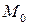нүктесінің функциясы үшін экстремаль нүкте болады. Бір айнымалы функцияның экстремумның қажетті шарты бойынша 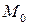-тің күдікті нүктесі екені шығады, немесе

функциясын қарастырып мынаны аламыз:

Мысал. 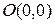нүктесі функциясының минимум нүктесі болады, себебі , ал басқа барлық нүктелерде . және , мына жүйе

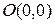күдікті нүктені береді.

Мысал. функциясының 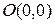нүктесі экстремаль нүктесі болмайды, себебі оның кез келген аймағында функция , егер -ден үлкен де, ал болғанда -ден кіші де мәндер қабылдайды. , болғандықтан координаталары мына жүйені , қанағатандырады, күдікті нүкте. Бұл мысалдан күдікті нүктенің экстремальдық нүкте болмауы да мүмкін.

гиперболалық параболоид, бұл функцияның графигінің түрі ертоқымның түрі сияқты, 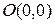- нүктесі ерекше нүкте болады.

Теорема 2 (экстремумның жеткілікті шарттары). 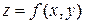функциясы өзінің күдікті нүктесінің кейбір аймағында 3 рет дифференциалданатын болсын. , , , деп белгілейік. Онда:

1) Егер болса, онда 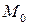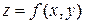үшін экстремаль нүктесі болады, егер болса, онда бұл – минимум нүктесі, ал гегр болса, онда 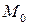- максимум нүктесі болады.

2) Егер болса, онда -нүктесінде экстремум жоқ.. болғанда экстремум табу үшін қосымша зерттеулер қажет. Дәлелдеусіз.

Мысал. функциясының экстремаль нүктелерімен экстремумдерін табайық.. , болғандықтан барлық үшін, критикалық нүктелерді табу үшін келесі теңдеулер жүйесін шешу керек:

. Бұдан екі шешуін аламыз және және екі , күдікті нүктелерді табамыз. Екінші ретті дербес туындыларды тауып және әрбір нүктені экстремумның жеткілікті шарты бойынша зерттейміз.

, , . а) . Бұл жағдайда:

; ; ; . Сондықтан нүктесінде экстремум жоқ.. б) . Бұл жағдайда: ; ; ; . экстремаль нүкте. болғандықтан, бұл – минимум нүктесі. нүктесіндегі функцияның мәні - функцияның минимумын береді.

Шартты экстремумдер.Айталық функцияның анықталу облысында қисығы теңдеуімен берілсін. функцияның шарты максимум нүктесі деп аталады, егер бұл нүктенің аймағы барлық осы аймақпен -ның қиылысуынан нүктелері үшін мына теңсіздік орындалса. Осы сияқты шарта минимум нүктесі мына теңсіздікпен анықталады.

Шарты максимум және минимум нүктелері шартты экстремум нүктелері, ал 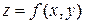функциясының осы нүктелердегі мәндері шартты экстремумдар (шартты максимум не шартты минимумдер) деп аталады. 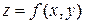функциясы теңіз деңгейінен биіктікті көрсетсе, онда бұл функциясының максимумы тау шыңына сәйкес. Егер жергілікті жерде соқпағы бар болса, онда 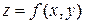функциясының шартты максимумын -де соқпақтағы теңіз деңгейінен ең жоғарғы биіктіктегі нүктелер сәйкес болады. Егер қисығы анықталған функция графигімен берілсе, онда 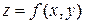функциясының шартты экстремумдерін табу бір айнымалы функцияның экстремумдерін табуға тіреледі.

Мысал. функциясының орындалғандығы экстремумын табу керек. Теңдеудң айқындалған түрде жазайық: және осыны функцияның орынына кояйық. , , . Осы бір айнымалы функцияның экстреумдерін табайық: ; болғандықтан бұл нүкте минимум нүктесі болады. функциясы нүктесінде шартты минимумге ие болады және ол мынаған тең: .

Шартты экстремумдарды табу үшін Лагранж әдісі. Бұл әдіс кез келген айнымалылар саны бар және кез келген шарттар саны үшін қолданылады. Бұл шартта экстремум табу есебін айнымалылар саны көп жаңа функциядан жай экстрамум табу есебіне әкеп тірейді. Келесі мысалда біз бұл әдісті екі айнымалы функция үшін көрсетеміз. теңдеуімен қисығы анықталып және ол 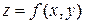-тің анықталу облысында жатсын. Лагранж функциясыдеп 3 айнымалының функциясын айтамыз , мұндағы –кез келген параметр.

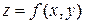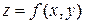Лагранж теоремасы. және функциялары нүктесінің аймағында дифференциалданатын болсын. нүктесі функциясының шарты орындалғандағы максимум (минимум) нүктесі болады, бірақ тек қана сол жағдайда, егер кейбір үшін нүктесі Лагранж функциясының максимум (минимум) нүктесі болса (дәлелдеусіз).

нүктесінде Лагранж функциясы экстремум мәнін қабылдасын. , функциялары үшін не білдіретінін көрейік. нүктесі функциясы үшін (күдікті) нүкте болғандықтан, экстремумнің қажетілік шарты бойынша, келесі теңдіктер дұрыс болады

немесе , соңғы теңдеуі нүктесі -қисығында жататынын көрсетеді.

теңдеулері шартты экстремум нүктесінде 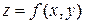, функцияларының градиенттері коллинеар екенін көрсетеді, немесе .

Мысал. Қабырғалары болатын параллелепипедтің бетінің ауданы -ға тең болғанда, максимал көлемін табу керек. Бұл есеп үш айнымалылы функцияның шарты орындалғанда максимумын табуға парапар. Лагранж функциясы – бұл жағдайда мына түрде болады: .

Функциясының күдікті нүктелерін табамыз, бірінші ретті дербес туындыларын 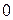-ге теңестіре отырып 4 белгісізі бар 4 теңдеулер жүйесін табамыз:

. Жүйенің бірінші теңдеуін 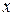-ке, екіншісін 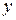-ке, үшіншісін -ке көбейтіп, оларды қосамыз, сонда .

Жүйенің 4-ші теңдеуін есепке ала отырып аламыз: немесе .

Табылған мәнін жұйенің алғашқы үш теңдеуіне қойып, 3 теңдеуі бар жүйені аламыз:

; ; . ескере отырып аламыз: . Осы үш теңдеуді өзара көбейтіп аламыз: ; . Осы теңдеуді 1,2,3 теңдеулерге бірінен соң біріне бөле отырып, мына өрнекті аламыз:

. Сонымен , параллелепипедтің максимал көлемі және ол параллелепипед қабырғасы кубке айналғанда орындалады.

Әдебиеттер: 9 нег.[244-248], 11 нег. [320-324].

Бақылау сұрақтар:

1. Экстремумның қажетті шарты.

2. Шартты экстремумдер.

3. Шартты экстремумдарды табу үшін Лагранж әдісі.

4. Лагранж теоремасы.

5. Мысал келтіру.