Производная показательной функции

Вывод формулы производной приведем на основе определения:

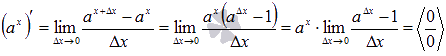
Пришли к неопределенности. Для ее раскрытия введем новую переменную 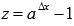, причем 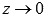при 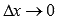. Тогда .

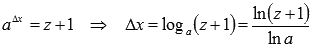В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел: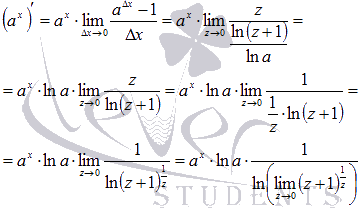

Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

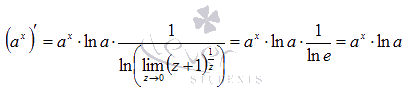
Производная логарифмической функции.

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем: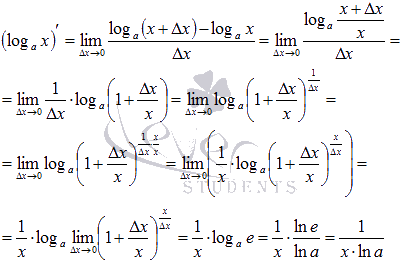

Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство 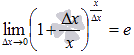справедливо в силу второго замечательного предела.