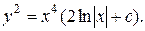Однородные дифференциальные уравнения первого порядка
1. Однородное уравнение первого порядка: определение и метод его решения
Определение 1.Уравнение первого порядка вида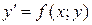 
называется однородным, если его правая часть 
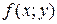является однородной функцией нулевого измерения, т.е. при любом 
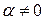справедливо равенство: 
.
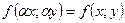Замечание 1. Уравнение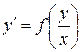 
является однородным, так как функция 
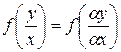удовлетворяет определению однородности нулевого измерения.
Определение 2.Уравнение вида
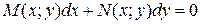
называется однородным, если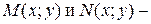 
однородные функции одного измерения однородности, т.е. 
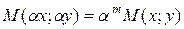и 
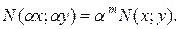
Метод решения однородного уравнения
Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены функции y(x) по формуле:
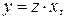
где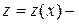 
новая функция, относительно которой и получится уравнение с разделяющимися переменными.
Решение однородного уравнения 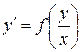в общем виде
замена: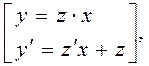 
После замены получается уравнение:
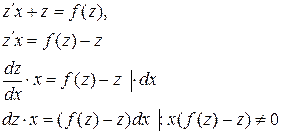
Разделим переменные и проинтегрируем полученное равенство:
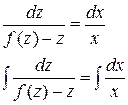
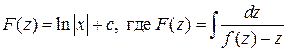
Выполнив обратную замену:
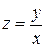
получим общий интеграл данного уравнения:
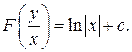
Далее необходимо проверить, не потеряны ли решения. Если уравнение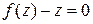 
имеет решения 
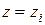, то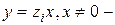 
решения уравнения 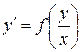,хотя при 
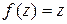данное уравнение принимает вид: 
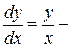уравнение c разделяющимися переменными, решение которого не составит большого труда.
Дифференциальные уравнения, приводящиеся к однородным
1) Уравнение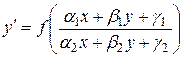 
приводится к однородному.
Для этого выполним замену:
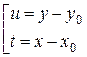
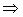
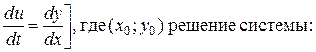
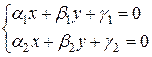если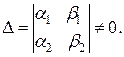 
После такой замены получается однородное уравнение относительно неизвестной функции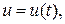 
в котором, выполняя замену: 
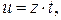получается уравнение с разделяющимися переменными.
Если же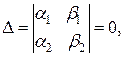 
то после замены: 
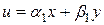исходное уравнение превращается в уравнение с разделяющимися переменными.
2) Некоторые ДУ возможно привести к однородным для новой, пока неизвестной функции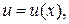 
если применить замену вида:
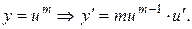
При этом число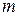 
подбирается из условия, чтобы полученное уравнение, если это возможно, стало однородным. Однако если это сделать невозможно, значит рассматриваемое ДУ привести к однородному таким способом нельзя.
Примеры с решениями
Пример 1.Решить уравнение:
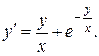
Решение. Данное уравнение имеет вид
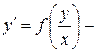однородное. Выполним замену:
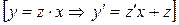
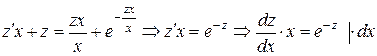
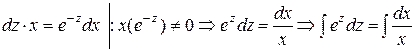
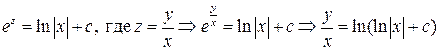
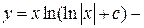общее решение уравнения.
При разделении переменных и делении на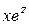 
могло быть потеряно решение 
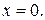Однако функция 
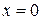не является решением данного уравнения.
Ответ: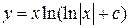 
Пример 2.Решить уравнение:
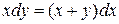
Решение. Проверим, что функции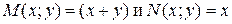 
являются однородными функциями 
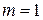измерения.
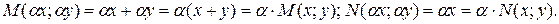
Следовательно, уравнение является однородным.
Выполним замену:
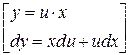
Тогда получим уравнение с разделяющимися переменными:
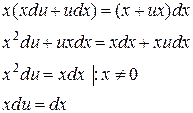
Разделим переменные:
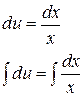
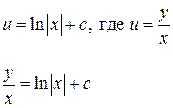
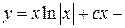общее решение уравнения
Прямой подстановкой в заданное уравнение убедимся, что 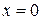является его решением, но оно было потеряно при делении уравнения на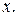 
Ответ: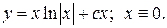 
Пример 3. Решить задачу Коши:
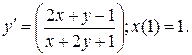
Решение. Покажем, что уравнение приводится к однородному уравнению.
Решим систему уравнений:
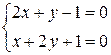
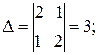
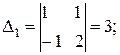
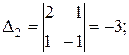
По правилу Крамера:
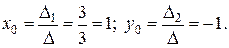
Сделаем замену:
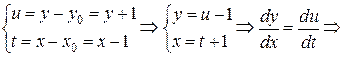
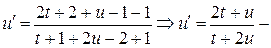однородное уравнение.
Замена:
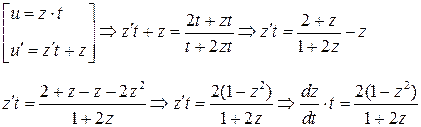
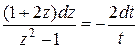
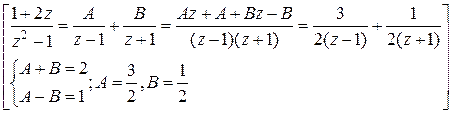
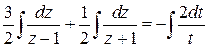
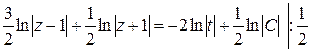
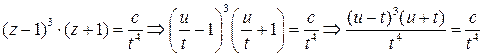
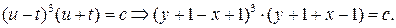
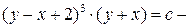общий интеграл данного уравнения
При разделении переменных могли быть потеряны решения при делении на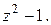 
Решим уравнение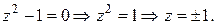 
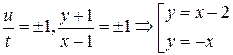
Однако эти функции входят в общий интеграл данного уравнения, при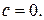 
Найдем решение задачи Коши, используя начальное условие 
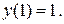Подставим в общий интеграл значения 
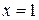и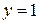 
:
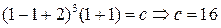
Таким образом частный интеграл данного уравнения, удовлетворяющий начальным условиям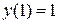 
, будет задаваться формулой:
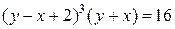
Ответ: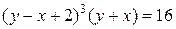 
Пример 4. Решить уравнение:
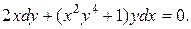
Решение. Покажем, что это уравнение приводится к однородному с помощью подстановки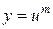 
и далее интегрируется с использованием замены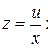 
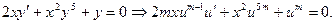
Полученное уравнение будет однородным, если показатели степеней пр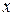и 
и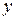 
равны между собой, то есть:
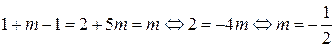
Выполним подстановку:
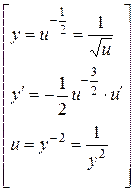
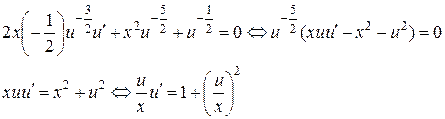
Получилось однородное уравнение. Сделаем замену:
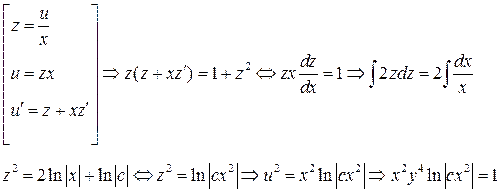
Получим общий интеграл данного уравнения. Однако заметим, что при разделении переменных было потеряно решение исходного уравнения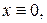 
которое надо добавить в ответ. Также было потеряно решение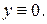 
Ответ: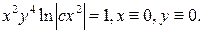 
Примеры
Решить уравнения или задачи Коши
1. 
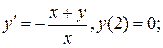
2. 
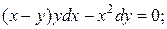
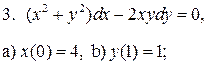
4. 
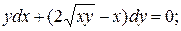
5. 
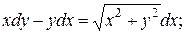
6. 
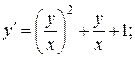
7. 
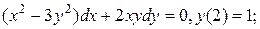
8. 
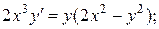
9. 
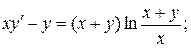
10. 
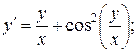
11. 
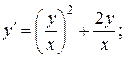
12. 
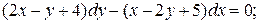
13. 
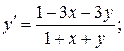
14. 
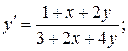
15. 
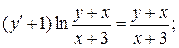
16. 
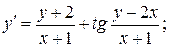
17. 
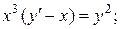
18. 
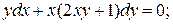
19. 
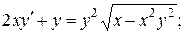
20. 
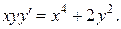
Ответы
1. 
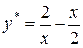
2. 
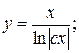
3. 
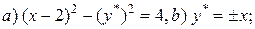
4. 
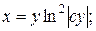
5. 
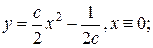
6. 
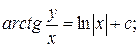
7. 
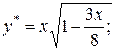
8. 
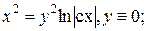
9. 
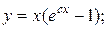
10. 
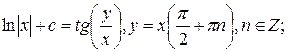
11. 
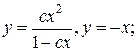
12. 
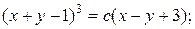
13. 
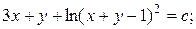
14. 
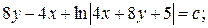
15. 
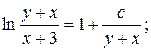
16. 
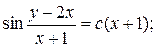
17. 
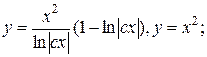
18. 
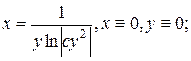
19. 
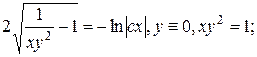
20. 