Задача С3. Определение усилий в стержнях плоской фермы
Для заданной плоской фермы, на узлы которой действует сила F, составляющая с горизонталью уголα, определить:
1) реакции опор фермы в точках А и В;
2) методом вырезания узлов усилия в стержнях фермы;
3) для 3-х стержней методом сечений (способом Риттера) проверить полученные результаты.
Необходимые для расчета данные приведены в табл.С3.
Таблица С3 Исходные данные для задачи С3.
| Вариант | ||||||||||
| α(град) | 30 | 30 | ||||||||
| F(Н) |
Пример С3.Дано: α = 300; F1 = 10 Н; F2 = 20 Н. Определить реакции опор фермы от заданной нагрузки и усилия в стержнях методом вырезания узлов; методом сечений проверить результаты вычислений в стержнях 1,3 и 4 (рис. С3).
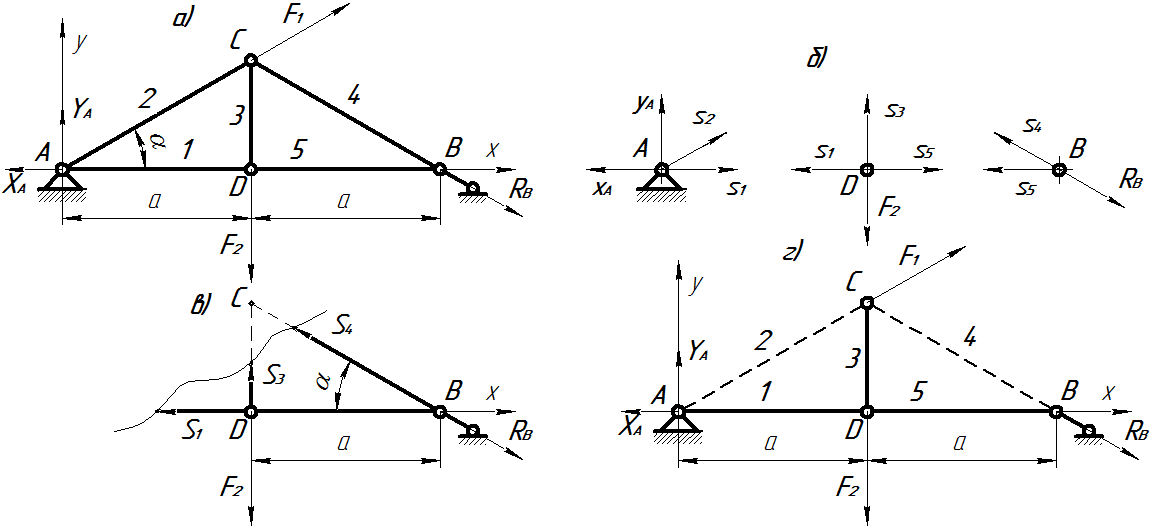 Рисунок С3
Рисунок С3
Решение
1. Для определения реакций опор рассмотрим равновесие фермы, на которую действует нагрузка: заданные (активные) силы F1 и F2; реакция шарнирно-неподвижной опоры ХА, YА; реакция стержня с шарнирами на концах RB (рис. С3,a).
2. Проводим оси координат ху и составляем уравнения равновесия сил и моментов для произвольной плоской системы сил:
 ; (1)
; (1)
 ; (2)
; (2)
 . (3)
. (3)
Реакцию RB определяем из уравнения (3):
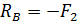 /
/ 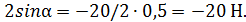
Реакцию ХА определяем из уравнения (1):
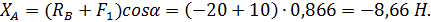
Реакцию УА определяем из уравнения (2):
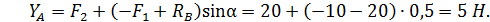
3. Определяем усилия в стержнях формы способом вырезания узлов (рис. 3,б). Предполагая, что стержни растянуты, направляем усилия в стержнях от узла. Расчет начнем с узла А, к которому приложены лишь две неизвестные силы S1 и S2.
Узел А: 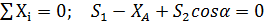 ; (4)
; (4)
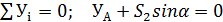 . (5)
. (5)
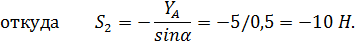
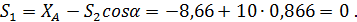
Узел Д: 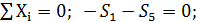
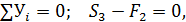 (6)
(6)
откуда  (7)
(7)
Узел В: 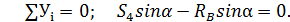
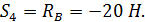
4. Методом сечений (способом Риттера) определяем усилия в стержнях 1, 3, и 4. Для этого мысленно разрезаем ферму по этим стержням и рассматриваем равновесие ее правой части (рис. С3,в). Составляем сумму моментов сил относительно точек пересечения линий действия неизвестных сил:
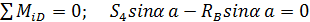 ; (8)
; (8)
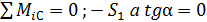 ; (9)
; (9)
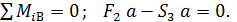 (10)
(10)
Откуда: 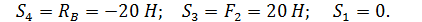
Ответ: 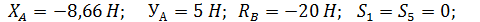
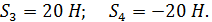
Знак (-) показывает, что данные стержни не растянуты, как предполагалось, а сжаты. Сжатые стержни 2 и 4 показаны штриховой линией, а растянутые – сплошной (рис. С3,г).
Задача С4. Равновесие сил с учетом трения покоя
Определить минимальное значение силы Р, прижимающей тормозную колодку к барабану весом G, и реакции опор механической системы в точках А и О. При окончательных расчетах принять: R = 2r; f = 0,2; а = 0,6 м; b = 0,4 м; e= 0,05 м. Другие необходимые для расчета данные приведены в табл. С4.
Таблица С4 Исходные данные для задачи С4.
| Вариант | ||||||||||
| Α(град) | 300 | 450 | 600 | 900 | 300 | 450 | 600 | 900 | 300 | 450 |
| Q(Н) |
Пример С4.Дано: α=30°; а = 0,6 м; b = 0,4 м; Q = 20 Н; f = 0,2; е = 0,05 м; R = 2r; G = 30 Н. Определить минимальное значение силы Р и реакции опор в точках А и О системы, находящейся в покое (рис. С4,а).
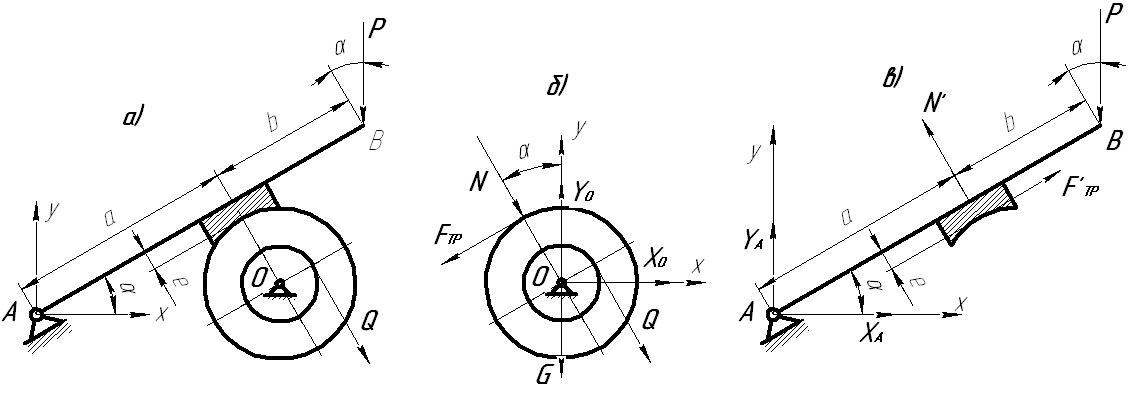
Рисунок С4
Решение
1. Рассмотрим равновесие сил, приложенных к барабану. На него действуют вес G, нормальная сила N со стороны тормозной колодки, сила трения Fтр,сила Q и реакции XO и YO в точке О. Составляем уравнения равновесия для этой произвольной плоской системы сил (рис. С4,б):
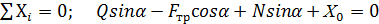 ; (1)
; (1)
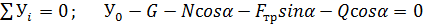 ; (2)
; (2)
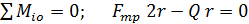 . (3)
. (3)
В состоянии предельного равновесия сила N минимальна, а сила трения (трения покоя) между тормозной колодкой и барабаном определяется по формуле
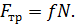 (4)
(4)
Из уравнений (1) – (4) получим
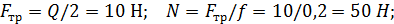
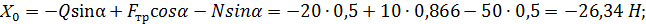
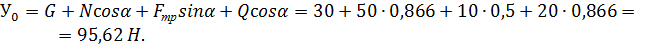
2. Для определения минимального значения силы Р, прижимающей тормозную колоду к барабану и реакций XА и YА в опоре А составляем уравнения равновесия сил, действующих на тормозную колодку (Рис. С4,в):
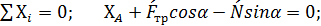 (5)
(5)
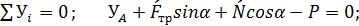 (6)
(6)
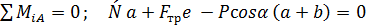 . (7)
. (7)
Откуда
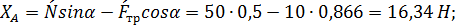
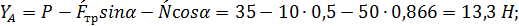
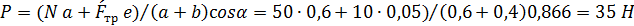 .
.
Ответ: 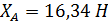 ;
; 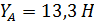 ;
; 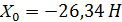 ;
; 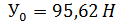 ;
; 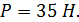 Знак (-) показывает, что реакция направлена в обратную сторону.
Знак (-) показывает, что реакция направлена в обратную сторону.
ДИНАМИКА
