Вычисление площадей плоских фигур
Лекция 7. Несобственные интегралы первого рода. Приложения интегралов: вычисление площадей, длин дуг и объёмов тел
Ранее рассматривались интегралы 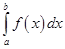 с конечными пределами
с конечными пределами 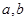 и от ограниченных функций
и от ограниченных функций 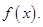 Если хотя бы одно из этих ограничений нарушается, то указанный интеграл будет несобственным. Такие интегралы часто встречаются в приложениях, поэтому перейдём к их изучению.
Если хотя бы одно из этих ограничений нарушается, то указанный интеграл будет несобственным. Такие интегралы часто встречаются в приложениях, поэтому перейдём к их изучению.
Несобственные интегралы
Сначала рассмотрим интегралы с бесконечными пределами.
Определение 1.Пусть функция 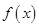 интегрируема на любом отрезке
интегрируема на любом отрезке 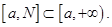 Тогда если существует конечный предел
Тогда если существует конечный предел 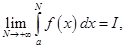 то говорят, что интеграл
то говорят, что интеграл 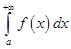 сходится. При этом пишут
сходится. При этом пишут 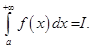 Если же указанный предел не существует или равен бесконечности, то говорят, что интеграл
Если же указанный предел не существует или равен бесконечности, то говорят, что интеграл 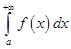 расходится.
расходится.
Аналогично определяются интегралы

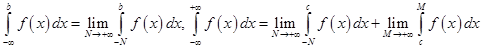
 ( здесь
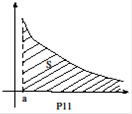
( здесь 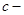 произвольная конечная точка). Эти интегралы называют несобственными интегралами первого рода. Их геометрический смысл ясен из рис. 11, где площадь
произвольная конечная точка). Эти интегралы называют несобственными интегралами первого рода. Их геометрический смысл ясен из рис. 11, где площадь 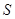
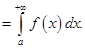 Теперь рассмотрим интегралы от неограниченных функций.
Теперь рассмотрим интегралы от неограниченных функций.
Определение 2.Если функция 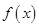 не ограничена в окрестности точки
не ограничена в окрестности точки 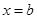 (её называют особой точкой ) и является интегрируемой на любом отрезке
(её называют особой точкой ) и является интегрируемой на любом отрезке 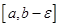
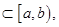 то по определению полагают
то по определению полагают 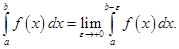 Если этот предел существует и конечен, то говорят, что интеграл
Если этот предел существует и конечен, то говорят, что интеграл 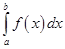 второго рода сходится. В противном случае он называется расходящимся. Аналогичный смысл имеют интегралы (второго рода)
второго рода сходится. В противном случае он называется расходящимся. Аналогичный смысл имеют интегралы (второго рода)
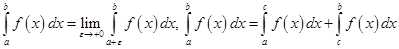 ,
,
где в первом случае точка 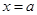 является особой, а во втором случае точка
является особой, а во втором случае точка 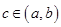 является особой. Поскольку заменой переменной
является особой. Поскольку заменой переменной 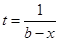 интеграл второго рода
интеграл второго рода 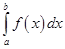 (
( 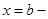 особая точка) сводится к интегралу первого рода, то будем изучать только интегралы с бесконечным верхним пределом. Сначала покажем, что эталонный интеграл
особая точка) сводится к интегралу первого рода, то будем изучать только интегралы с бесконечным верхним пределом. Сначала покажем, что эталонный интеграл
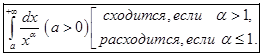
Действительно, имеем
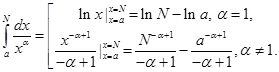
Переходя здесь к пределу при 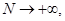 получаем наше утверждение. С помощью эталонного интеграла можно исследовать сходимость других несобственных интегралов.
получаем наше утверждение. С помощью эталонного интеграла можно исследовать сходимость других несобственных интегралов.
Теорема сравнения 1.Пусть функции 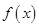 и
и 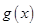 интегрируемы на произвольном отрезке
интегрируемы на произвольном отрезке 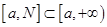 и имеют место неравенства
и имеют место неравенства 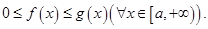 Тогда если сходится интеграл
Тогда если сходится интеграл 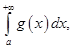 то и сходится интеграл
то и сходится интеграл 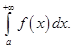 Если же интеграл
Если же интеграл 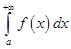 расходится, то и расходится интеграл
расходится, то и расходится интеграл 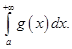
Теорема сравнения 2. Пусть функции 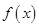 и
и 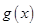 положительны иинтегрируемы на произвольном отрезке
положительны иинтегрируемы на произвольном отрезке 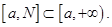 Пусть, кроме того, существует предел
Пусть, кроме того, существует предел 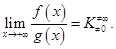 Тогда интегралы
Тогда интегралы 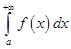 и
и 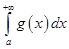 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Замечание 1. При примененииэтих теорем часто используется таблица эквивалентных бесконечно малых:
Если 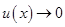 при
при 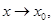 то при
то при 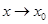 верны следующие соотношения:
верны следующие соотношения:
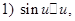
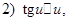
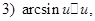
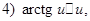

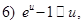
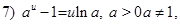
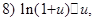
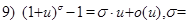 const.
const.
Например, интеграл 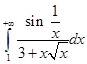 сходится, так как
сходится, так как 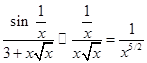 и интеграл
и интеграл 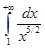 сходится (см. эталонный интеграл(
сходится (см. эталонный интеграл( 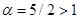 ) и теорему сравнения 2).
) и теорему сравнения 2).
Отметим, что теоремы сравнения верны лишь для неотрицательных подынтегральных функций. Если эти функции не являются знакопостоянными, то вводят понятие абсолютной сходимости: говорят, что интеграл 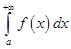 сходится абсолютно, если сходится интеграл
сходится абсолютно, если сходится интеграл 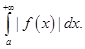 Если последний интеграл расходится, а сам интеграл
Если последний интеграл расходится, а сам интеграл 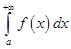 сходится, то его называют условно сходящимся интегралом. Нетрудно показать, что из сходимости интеграла
сходится, то его называют условно сходящимся интегралом. Нетрудно показать, что из сходимости интеграла 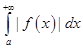 вытекает обычная сходимость интеграла
вытекает обычная сходимость интеграла 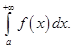 Обратное, вообще говоря, неверно. Можно показать, например, что интеграл
Обратное, вообще говоря, неверно. Можно показать, например, что интеграл 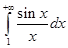 сходится, а интеграл
сходится, а интеграл 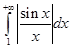 расходится. Тем не менее, при исследовании сходимости интегралов от знакопеременных функций изучают сначала их абсолютную сходимость (здесь можно применить теоремы сравнения), а затем – условную сходимость.
расходится. Тем не менее, при исследовании сходимости интегралов от знакопеременных функций изучают сначала их абсолютную сходимость (здесь можно применить теоремы сравнения), а затем – условную сходимость.
Например, рассмотрим интеграл 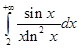 . Здесь подынтегральная функция изменяет знак на полуинтервале
. Здесь подынтегральная функция изменяет знак на полуинтервале 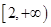 , поэтому применить к нему теоремы сравнения нельзя. Рассмотрим “модульный” интеграл
, поэтому применить к нему теоремы сравнения нельзя. Рассмотрим “модульный” интеграл 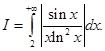 Здесь подынтегральная функция неотрицательна, и поэтому к этому интегралу можно применить теорему сравнения 1:
Здесь подынтегральная функция неотрицательна, и поэтому к этому интегралу можно применить теорему сравнения 1:
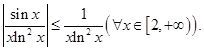
Так как интеграл 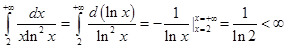 сходится, то и интеграл
сходится, то и интеграл 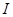 также сходится, а, значит, исходный интеграл
также сходится, а, значит, исходный интеграл 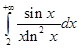 сходится абсолютно.
сходится абсолютно.
Вычисление площадей плоских фигур
Из геометрического смысла определённого интеграла вытекает следующее утверждение.
Теорема 1.Если фигура 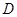 задана неравенствами
задана неравенствами 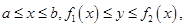 где функции
где функции 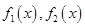 непрерывны на отрезке
непрерывны на отрезке 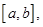 то площадь этой фигуры вычисляется по
то площадь этой фигуры вычисляется по
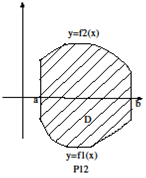 формуле
формуле 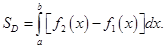 Если фигура ограничена линиями
Если фигура ограничена линиями  причём функция
причём функция  знакопеременна и непрерывна на отрезке
знакопеременна и непрерывна на отрезке 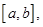 то её площадь равна
то её площадь равна 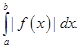
Действительно, фигуру 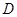 можно перенести параллельно оси
можно перенести параллельно оси 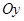 вверх и тогда она будет сверху и снизу ограничена линиями
вверх и тогда она будет сверху и снизу ограничена линиями
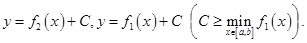
Поэтому 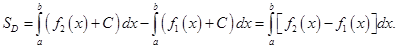
Переходя к вычислению площади в полярных координатах, напомним, что любая точка
 на плоскости вполне однозначно определяется своим полярным радиусом
на плоскости вполне однозначно определяется своим полярным радиусом 
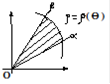
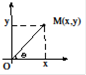
 и полярным углом
и полярным углом 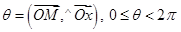 (считаем, что началу координат
(считаем, что началу координат 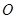 соответствует радиус
соответствует радиус 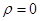 и любой фиксированный полярный угол
и любой фиксированный полярный угол 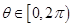 ). Поэтому любую кривую на плоскости можно задать уравнением
). Поэтому любую кривую на плоскости можно задать уравнением 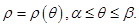 Переход от декартовых координат точки
Переход от декартовых координат точки 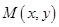 к полярным осуществляется по формулам
к полярным осуществляется по формулам
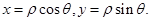
Теорема 2.Пусть фигура 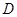 задана в полярных координатах неравенствами
задана в полярных координатах неравенствами 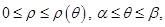 причём функция
причём функция 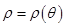 непрерывна на отрезке
непрерывна на отрезке 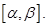 Тогда площадь этой фигуры вычисляется по формуле
Тогда площадь этой фигуры вычисляется по формуле 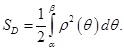 Если фигура описывается неравенствами
Если фигура описывается неравенствами
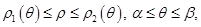
причём функции 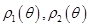 непрерывны на отрезке
непрерывны на отрезке 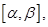 то её площадь вычисляется по формуле
то её площадь вычисляется по формуле 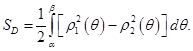
Площади фигур с замкнутой границей удобно вычислять, если граница задана в параметрической форме.
Теорема 3.Пусть фигура 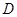 имеет границу
имеет границу 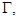 заданную параметрически уравнениями
заданную параметрически уравнениями
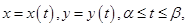 причём при возрастании параметра
причём при возрастании параметра 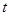 от
от 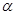 к
к 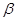 обход границы
обход границы 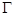 совершается так, что сама область
совершается так, что сама область 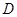 остаётся слева от наблюдателя. Если при этом функции
остаётся слева от наблюдателя. Если при этом функции 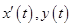 непрерывны на отрезке, то площадь этой фигуры вычисляется по формуле
непрерывны на отрезке, то площадь этой фигуры вычисляется по формуле 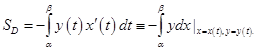 (здесь
(здесь 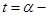 начало обхода,
начало обхода, 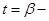 конец обхода границы
конец обхода границы 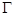 ).
).
3. Вычисление длины дуги
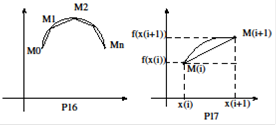 Пусть на плоскости
Пусть на плоскости 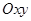 задана некоторая незамкнутая кривая
задана некоторая незамкнутая кривая  (см. рис. Р16). Произведём разбиение
(см. рис. Р16). Произведём разбиение
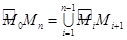
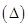
этой дуги на частичные дуги 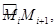 в каждую из которых впишем хорду
в каждую из которых впишем хорду 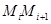 . Тогда получим ломанную
. Тогда получим ломанную 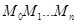 , вписанную в дугу
, вписанную в дугу 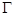 . Пусть
. Пусть 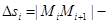 длина хорды
длина хорды 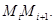
Определение 3.За длину дуги 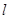 кривой
кривой 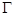 принимают предел, к которому стремится периметр ломанной, вписанной в эту дугу, при стремлении длины максимального звена этой ломанной к нулю, т. е.
принимают предел, к которому стремится периметр ломанной, вписанной в эту дугу, при стремлении длины максимального звена этой ломанной к нулю, т. е. 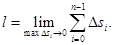 Если кривая
Если кривая 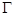 замкнутая, то разбивают её двумя несовпадающими точками на две незамкнутые кривые
замкнутая, то разбивают её двумя несовпадающими точками на две незамкнутые кривые 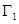 и
и 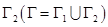 и тогда
и тогда
дл. 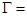 дл.
дл. 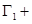 дл.
дл. 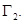
Теорема 4. Если дуга 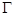 задана уравнением
задана уравнением 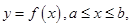 где функция
где функция 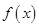 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 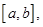 то её длина вычисляется по формуле
то её длина вычисляется по формуле
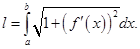
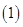
Доказательство. Произведём разбиение 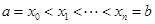 отрезка
отрезка 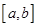 на частичные отрезки
на частичные отрезки 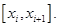 Это разбиение порождает разбиение
Это разбиение порождает разбиение  дуги
дуги  частичные дуги
частичные дуги 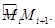 По определению 3 имеем
По определению 3 имеем 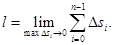 Длина хорды
Длина хорды 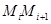 равна (см. рис. Р17) величине
равна (см. рис. Р17) величине
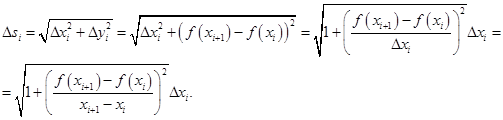
По теореме Лагранжа существует точка 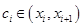 такая, что
такая, что
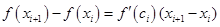
поэтому 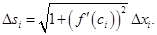 Учитывая это, получаем, что
Учитывая это, получаем, что
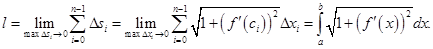
Теорема доказана.
Замечание 2.Величина 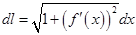 называется дифференциалом дуги
называется дифференциалом дуги 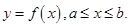 Учитывая, что
Учитывая, что 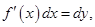 её можно записать в виде
её можно записать в виде 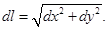 Мы получили теорему Пифагора для криволинейного треугольника с катетами
Мы получили теорему Пифагора для криволинейного треугольника с катетами 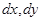 и “гипотенузой”
и “гипотенузой” 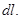 Теперь формулу (1) для вычисления длины дуги можно записать кратко так:
Теперь формулу (1) для вычисления длины дуги можно записать кратко так: 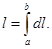 Эта форма записи длины дуги особенно удобна, если дуга
Эта форма записи длины дуги особенно удобна, если дуга 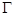 задана параметрически или в полярной форме. Из неё можно получить следующие утверждения.
задана параметрически или в полярной форме. Из неё можно получить следующие утверждения.
Теорема 5. Если дуга 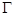 задана параметрически уравнениями
задана параметрически уравнениями 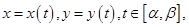 где функции
где функции 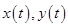 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке 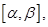 то её длина вычисляется по формуле
то её длина вычисляется по формуле
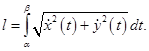
Если дуга 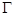 задана в полярных координатах уравнением
задана в полярных координатах уравнением 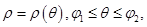 где функция
где функция 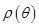 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 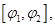 то её длина вычисляется по формуле
то её длина вычисляется по формуле 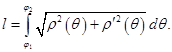
Действительно, если 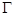 задана в параметрической форме, то
задана в параметрической форме, то
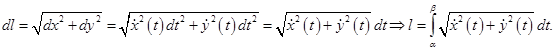
Рекомендуем получить формулу длины дуги в полярных координатах самостоятельно.
Например, если дуга 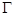 задана уравнением
задана уравнением 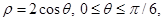 то её длина равна
то её длина равна
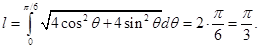
Вычисление объёмов тел
С помощью определённого интеграла можно вычислять и объёмы тел. Дадим соответствующие формулы.
 Теорема 6.Пусть тело
Теорема 6.Пусть тело 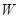 заключено между плоскостями
заключено между плоскостями 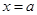 и
и 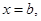 а
а 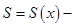 площадь его поперечного сечения плоскостью
площадь его поперечного сечения плоскостью 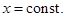 Если функция
Если функция 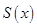 непрерывна на отрезке
непрерывна на отрезке 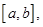 то объем тела
то объем тела 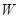 вычисляется по формуле
вычисляется по формуле

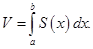
Доказательство.Произведём разбиение отрезка 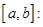
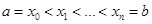
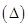
на частичные отрезки 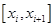 и обозначим
и обозначим 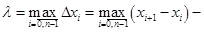 диаметр разбиения
диаметр разбиения 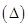 . Плоскости
. Плоскости 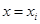 разобьют тело
разобьют тело 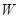 на тела
на тела 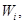 которые можно приближённо считать прямыми круговыми цилиндрами высотой
которые можно приближённо считать прямыми круговыми цилиндрами высотой 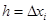 и основаниями – кругами площади
и основаниями – кругами площади 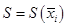 , где
, где 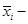 произвольная фиксированная точка отрезка
произвольная фиксированная точка отрезка 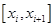 ,
, 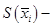 площадь поперечного сечения плоскостью
площадь поперечного сечения плоскостью 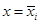 . Объем тела
. Объем тела 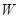 приближённо равен сумме объёмов тел
приближённо равен сумме объёмов тел 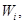 т.е.
т.е. 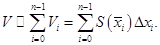 Это равенство будет те точнее, чем мельче разбиение
Это равенство будет те точнее, чем мельче разбиение 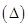 , и при
, и при 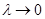 оно становится точным, т.е.
оно становится точным, т.е.
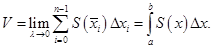
Теорема доказана.
Замечание 3.Если тело 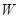 получено вращением криволинейной трапеции
получено вращением криволинейной трапеции
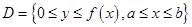
вокруг оси 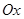 , то объем этого тела вычисляется по формуле
, то объем этого тела вычисляется по формуле
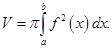
Действительно, в этом случае поперечное сечение является кругом радиуса 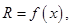 поэтому
поэтому 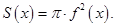 Аналогично вычисляется объем тела, полученного вращением вокруг оси
Аналогично вычисляется объем тела, полученного вращением вокруг оси  криволинейной трапеции
криволинейной трапеции 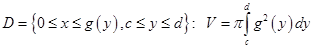 (конечно, в выписанных формулах для
(конечно, в выписанных формулах для 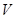 предполагается, что функции
предполагается, что функции 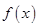 и
и 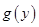 непрерывны на соответствующих отрезках).
непрерывны на соответствующих отрезках).
