Электрический колебательный контур

4.2.1. Колебательный контур состоит из катушки индуктивностью L = 1 мГн и конденсатора емкостью С = 2 нФ. Пренебрегая сопротивлением контура, определите, на какую длину волны этот контур настроен.

4.2.2. Колебательный контур радиоприемника настроен на частоту 9 МГц. Во сколько раз следует изменить емкость конденсатора колебательного контура, чтобы приемник был настроен на волну 50м?

4.2.3. В колебательном контуре зависимость напряжения на конденсаторе описывается уравнением 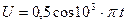(все величины даны в СИ). Определить частоту колебаний и емкость конденсатора, если максимальная энергия равна 5·10^-4 Дж.

4.2.4. Колебательный контур состоит из катушки индуктивностью L=0,2мГн и конденсатора площадью пластин S = 155 см², расстояние между которыми d = 1,5 мм. Зная, что контур резонирует на длину волны λ = 630 м, определите диэлектрическую проницаемость среды, заполняющей пространство между пластинами конденсатора.

4.2.5. Колебательный контур состоит из катушки индуктивностью L = 0,1 Гн и конденсатора емкостью С = 39,5 мкФ. Заряд конденсатора Q_m=3мкКл. Пренебрегая сопротивлением контура, запишите уравнение: 1)изменения силы тока в цепи в зависимости от времени; 2) изменения напряжения на конденсаторе в зависимости от времени.

4.2.6. Сила тока в колебательном контуре, содержащем катушку индуктивностью L = 0,1 Гн и конденсатор, со временем изменяется согласно уравнению 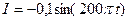, А. Определите: 1) период колебаний; 2) емкость конденсатора; 3) максимальное напряжение на обкладках конденсатора; 4) максимальную энергию магнитного поля; 5) максимальную энергию электрического поля.

4.2.7. Сила тока в колебательном контуре изменяется со временем по закону 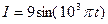А. Емкость контура 0,5 мкФ. Найти индуктивность контура и амплитудное значение напряжения на конденсаторе.

4.2.8. Напряжение на обкладках конденсатора в колебательном контуре изменяется по закону U = 50cos(10⁴πt) В. Емкость конденсатора 0,1 мкФ. Найти период колебаний, индуктивность контура и амплитудное значение силы тока.

4.2.9. Уравнение изменения со временем силы тока в колебательном контуре имеет вид I = 0,02sin(400πt) А. Индуктивность контура 1 Гн. Найти период колебаний, емкость контура, максимальную энергию электрического поля.

4.2.10. Колебательный контур состоит из конденсатора емкостью 25 нФ и катушки индуктивностью 1 Гн. Максимальный заряд на обкладках конденсатора 2,5 мкКл. Записать уравнение для изменения со временем разности потенциалов на обкладках конденсатора и силы тока в контуре.

4.2.11. Энергия свободных незатухающих колебаний, происходящих в колебательном контуре, составляет 0,2 мДж. При медленном раздвигании пластин конденсатора частота колебаний увеличилась в п=2 раза. Определите работу, совершенную против сил электрического поля.

4.2.12. Конденсатор емкостью С зарядили до напряжения U_m и замкнули на катушку индуктивностью L. Пренебрегая сопротивлением контура, определите амплитудное значение силы тока в данном колебательном контуре.

4.2.13. Колебательный контур содержит катушку с общим числом витков N=100 и индуктивностью L=10 мкГн и конденсатор емкостью С=1 нФ. Максимальное напряжение U_m на обкладках конденсатора составляет 100 В. Определите максимальный магнитный поток, пронизывающий катушку.

Волны

4.3.1. Плоский источник колебаний осуществляет колебания по закону s=5sin3140t мм. Скорость распространения колебаний равна 340 м/с. Определить смещение от положения равновесия и скорость частиц среды, которые расположены на расстоянии 170 м от источника колебаний, через 2 с после начала колебаний источника.

4.3.2. Волна распространяется в упругой среде со скоростью 300 м/с. Наименьшее расстояние между точками, фазы колебаний которых противоположны, равно 1 м. Определить частоту колебаний и длину волны.

4.3.3. Определить разность фаз колебаний двух точек среды, расположенных на расстоянии 10 см друг от друга, если в среде распространяется плоская волна вдоль линии, соединяющей эти точки. Скорость распространения волны 340 м/с, частота колебаний 1000 Гц.

4.3.4. Напряженность электрического поля между обкладками открытого колебательного контура, являющимся источником плоской электромагнитной волны, изменяется по закону Е = 200cos10⁵t В/м. Определить напряженность электрического поля, удаленных от источника на 30 км, через 0,3 с после начала колебаний.

4.3.5. Плоская звуковая волна с частотой колебаний 500 Гц и амплитудой колебаний 0,3 мм распространяется в воздухе. Длина волны 70 см. Определить скорость распространения колебаний и максимальную скорость частиц воздуха.

4.3.6. Смещение от положения равновесия точки, находящейся на расстоянии 4 см от плоского источника колебаний, в момент времени равный 1/6 периода колебаний, составляет половину амплитуды. Определить длину волны. Колебания происходят по закону синуса.

4.3.7. От источника колебаний распространяется плоская волна с амплитудой колебаний 1 см. Определить смещение частиц от положения равновесия в точке, удаленной от источника на ¾ длины волны, в момент времени, когда от начала колебаний прошло время, равное 0,9 периода.

4.3.8. Две точки лежат на луче и находятся от источника колебаний на расстоянии x₁ = 4 м и х₂ = 7 м. Период колебаний Т = 20 мс и скорость υ распространения волны равна 300 м/с. Определите разность фаз колебаний этих точек.

4.3.9. Волна распространяется в упругой среде со скоростью υ = 150 м/с. Определите частоту ν колебаний, если минимальное расстояние Δх между точками среды, фазы колебаний которых противоположны, равно 0,75 м.

4.3.10. Звуковые колебания с частотой ν = 450 Гц и амплитудой А = 0,3 мм распространяется в упругой среде. Длина волны λ = 80 см. Определите: 1)скорость распространения волн; 2) максимальную скорость частиц среды.

4.3.11. Плоская синусоидальная волна распространяется вдоль прямой, совпадающей с положительным направлением оси х в среде, не поглощающей энергию, со скоростью υ = 10 м/с. Две точки, находящиеся на этой прямой на расстоянии х₁ = 7 м и х₂ = 10 м от источника колебаний, колеблются с разностью фаз Δφ = 3π/5. Амплитуда волны А = 5 см. Определите: 1) длину волны λ; 2) уравнение волны; 3) смещение ξ₂ второй точки в момент времени t₂ = 2 с.

4.3.12. Скорость распространения электромагнитных волн в некоторой среде составляет υ = 250 Мм/с. Определите длину волны электромагнитных волн в этой среде, если их частота в вакууме ν₀ = 1 МГц.

4.3.13. В упругой среде распространяется волна со скоростью 20 м/с. Частота колебаний 2 с^-1, амплитуда 0,02 м. Определите длину волны, фазу колебаний, смещение, скорость, ускорение точки, отстоящей на расстоянии 60 м от источника в момент времени t = 4 с.

4.3.14. Волна распространяется со скоростью 20 м/с. Две точки, находящиеся на прямой на расстоянии 12 и 15 м от источника колебаний, колеблются по закону синуса с амплитудами равными 0,1 м и с разностью фаз 135°. Найти длину волны, написать уравнение волны и найти смещение указанных точек в момент времени t = 1,2 с.

4.3.15. Определить скорость υ распространения волны в упругой среде, если разность фаз Δφ колебаний двух точек, отстоящих друг от друга на Δх=18 см, равна 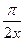. Частота колебаний ν=25 Гц.

4.3.16. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны равна 1 мА/м. Определите амплитуду напряженности электрического поля волны.

4.3.17. Определить разность фаз Δφ колебаний двух точек, лежащих на луче и на расстоянии Δl=1м, если длина волны х=0,5м.

4.3.18. Волна распространяется со скоростью 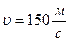. Определить частоту ν колебаний, если минимальное расстояние Δх между точками среды, фазы которых противоположно равно 1 м.

4.3.19. Звуковые колебания с частотойν=450 Гц и амплитудой А=0,3 мм распространяются в упругой среде. Длина волны l=80 см. Определить: 1) скорость распространения волн; 2) максимальную скорость частиц среды.

4.3.20. Две точки лежат на луче и находятся на расстоянии х₁=4м и х₂=7м. Период колебаний Т=20мс и скорость распространения волны равна 300 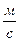. Определить разность фаз колебаний этих точек.

4.3.21. Плоская синусоидальна волна распространяется вдоль прямой совпадающей с положительным направлением оси х в среде, не поглощающей энергию, со скорость υ=10 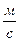. Две точки находящиеся на этой прямой на расстоянии х₁=7м и х₂=10м от источника колебаний, колеблются с разностью фаз 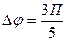, Амплитуда волны А=5см. Определить: 1) длину волны l; 2)уравнение волны; 3)смещение у_х второй точки в момент времени t=2с.

4.3.22. Поперечная волна распространяется вдоль упругого шнура со скоростью υ=10 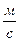. амплитуда колебаний частиц шнура А=5 см, а период колебаний Т=1с. Запишите уравнение волны и определите: 1) длину волны; 2) фазу колебаний, смещение, скорость и ускорение точки, находящейся на расстоянии х=9 м от источника колебаний в момент времени t = 2,5с.

4.3.23. Определить скорость u распространения волны в упругой среде, если разность фаз Dj колебания двух точек, находящихся на расстоянии Dх=24 см, равна p/2. Период колебаний Т=4∙10^-3 с.

4.3.24. Плоская волна распространяется вдоль оси Х со скоростью u=300 м/с. Амплитуда колебаний равна 0,6 мм. Длина волны l=0,3м. Записать уравнение волны.

4.3.25. Определить минимальное расстояние между двумя точками на оси Х, если разность фаз колебаний в этих точках Dj=p, если скорость распространения волны u=150 м/с, а период колебаний Т=0,01с.

4.3.26. Уравнение плоской волны, распространяющейся вдоль оси Х у=0,02cos∙sin314(t-0,002x)см. Определить амплитуду, частоту, период колебаний и скорость распространения волны.

4.3.27. Плоский источник колебаний создает колебания по закону у=0,1cos628t мм. Скорость распространения колебаний u=170 м/с. На каком расстоянии от источника находится точка, в которой смещение у=0,1мм в момент времени t=0,5с?

Дифракция света

4.4.1. На дифракционную решетку, имеющую 600 штрихов на 1 мм, нормально падает свет от газоразрядной трубы. Дифракционный спектр рассматривается через зрительную трубу. Красная линия в спектре первого порядка видна под углом 23⁰, зеленая - под углом 19⁰. Определить длины волн этих линий.

4.4.2. Как изменится картина дифракционного спектра, если решетку с периодом 0,02 мм заменить решеткой с периодом 0,01 мм ?

4.4.3. Найти наибольший порядок спектра для белого света (400-700 нм), если постоянная дифракционной решетки равна 2,0 мкм.

4.4.4. Чему равна постоянная дифракционной решетки, если, для того чтобы увидеть красную линию (l=7×10⁷м) в спектре второго порядка, зрительную трубу установили под углом 30⁰. Какое число штрихов нанесено на 1 см длины этой решетки? Свет падает на решетку нормально.

4.4.5. Сколько штрихов на 1 мм длины имеет дифракционная решетка, если зеленая лилия ртути (l=0,55 мкм) в спектре первого порядка наблюдается под углом 20⁰?

4.4.6. На дифракционную решетку нормально падает пучок света. Угол дифракции для натриевой лилии (l=0,59 мкм) в спектре первого порядка 18⁰. Некоторая линия дает в спектре второго порядка угол дифракции 24⁰. Найти длину волны этой линии и число штрихов на 1 мм решетки.

4.4.7. На дифракционную решетку нормально падает пучок света от разрядной трубки. Чему должна быть равна постоянная дифракционной решетки, чтобы в направлении j=41⁰ совпадали максимумы двух линий: l₁=0,66 мкм и l₂=0,41 мкм ?

4.4.8. На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной гелием. На какую линию в спектре третьего порядка накладывается красная линия гелия (l=6,7×10^{-5 см) спектра второго порядка?}

4.4.9. Найти наибольший порядок спектра для желтой линии натрия l=0,59 мкм, если постоянная дифракционной решетки 2 мкм.

4.4.10. На дифракционную решетку нормально падает пучок монохроматического света. Максимум третьего порядка наблюдается под углом 36⁰ к нормали. Найти постоянную решетки, выраженную в длинах волн падающего света.

4.4.11. Чему равна постоянная дифракционной решетки, если в первом порядке линия спектра калия l₁=0,404 мкм и видна под углом 15⁰?.

4.4.12. Под каким углом в спектре второго порядка видны линии дублета натрия l₁=0,599 мкм и l₂=0,590 мкм, если постоянная решетки d=0,001 мм?

4.4.13. На дифракционную решетку, имеющую 100 штрихов на миллиметр, падает плоская монохроматическая волна (l=5×10^{-7 м). Определить наибольший порядок спектра, который можно наблюдать при нормальном падении лучей на решетку.}

4.4.14. На дифракционную решетку, имеющую период 1,2×10^{-3 см, нормально падает монохроматическая волна. Оценить длину волны, если угол между спектрами второго и третьего порядка} Dj=2⁰.

4.4.15. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (l=0,6 мкм) максимум пятого порядка отклонен на угол j=18⁰?

4.4.16. На дифракционную решетку, содержащую n=100 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на Dj=20⁰. Определить длину волны света.

4.4.17. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на j₁=14⁰. На какой угол отклонен максимум третьего порядка?

4.4.18. Дифракционная решетка содержит n=200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (l=0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?

4.4.19. На дифракционную решетку, содержащую 400 штрихов на 1 мм, падает нормально монохроматический свет (l=0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Найти угол дифракции, соответствующий последнему максимуму.

4.4.20. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (l=0,4 мкм) спектра третьего порядка?

4.4.21. На дифракционную решетку с периодом d=10 мкм под углом 30⁰ падает монохроматический свет с длиной волны 600 пм. Определить угол дифракции, соответствующий второму главному максимуму.

4.4.22. Определить угол отклонения лучей зеленого света (l=0,55 мкм) в спектре первого порядка, полученном с помощью дифракционной решетки, период которой равен 0,02 мм.

4.4.23. Дифракционная решетка содержит 120 штрихов на 1 мм. Найти длину волны монохроматического света, падающего па решетку, если угол между двумя спектрами первого порядка равен 8⁰.

4.4.24. Для определения периода решетки на нее направили световой пучок через красный светофильтр, пропускающий лучи с длиной волны 0,76 мкм. Каков период решетки, если на экране, отстоящем от решетки на 1 м, расстояние между спектрами первого порядка 15,2 см?

4.4.25. Определить постоянную дифракционной решетки, если угол между двумя спектрами третьего порядка для натрия 4⁰. Длина волны 0,589 мкм.

Тепловое излучение

4.5.1. Найти температуру печи, если из ее окошка площадью 5 см² излучается в секунду 200 Дж энергии. (1630° К)

4.5.2. При какой температуре максимум энергии в спектре абсолютно черного тела приходится на длину волны 580 нм? (5000° К)

4.5.3. Средняя температура поверхности Земли +10°С. Определить длину волны, на которую приходится максимум земного излучения, если Землю принять за абсолютно черное тело. (10,1 мкм)

4.5.4. На какую длину волны приходится максимум излучения Солнца, если температура Т его поверхности равна 5790° К? (0,5 мкм)

4.5.5. На какую длину волны приходится максимум энергии в спектре излучения абсолютно черного тела, имеющего температуру 0° С? (10,6 мкм)

4.5.6. Длина волны, соответствующая максимуму энергии в спектре абсолютно черного тела, равна 722 нм. Излучающая поверхность тела равна 4 см². Определить мощность излучения. (5,9 кВт)

4.5.7. Из смотрового окошечка печи площадью в 3 см² за 1 сек излучается 17 Дж энергии. Считая, что окошечко излучает как абсолютно черное тело, определить температуру печи. (1000° К)

4.5.8. Вследствие лучеиспускания Земля теряет 90,7 Дж в секунду с каждого квадратного метра своей поверхности. При какой температуре такое же количество энергии излучал бы 1 м² поверхности абсолютно верного тела? (200° К)

4.5.9. Какую температуру имеет абсолютно черное тело, излучающее 9,32 Дж энергии в минуту с 1 см²? (400° К)

4.5.10. Определить энергетическую светимость* Солнца, приняв его за абсолютно черное тело с температурой поверхности 6000° К. (73500 кВт/м²).

4.5.11. Радиаторы отопления были нагреты от t₁ = 27⁰С до t₂ = 87°С. Во сколько раз увеличилась энергетическая светимость радиаторов? Принять радиаторы за абсолютно черные тела. (В 2 раза)

4.5.12. Температура абсолютно черного тела 127° С. Какова будет его температура, если энергетическая светимость возрастет в 4 раза? (292° С)

4.5.13. Во сколько раз увеличится энергетическая светимость абсолютно черного тела при его нагревании от 27° С до 327° С? (в 16 раз)

4.5.14. Какое количество энергии излучает с площади S = 0,5 м^г абсолютно черное тело при температуре t = 727°С в течение 1 мин? (1,7×10⁶ Дж)

4.5.15. Определить температуру печи, если из смотровою окошка площадью S=10 см¹ в 1 сек излучается энергия Е = 907,2 Дж. Излучение окошка принять за излучение абсолютно черного тела. (1727° С)

4.5.16. Максимум энергии излучения абсолютно черного тела приходится на длину волны 1 мкм На какую длину волны он сместится, если температура тела уменьшится на 900°? (1,45 мкм)

4.5.17. Максимум энергии излучения абсолютно черного тела приходится на длину волны l = 2,9 мкм. Вычислить энергетическую светимость этого тела. (5,67×10⁴ Вт/м²)

4.5.18. Вычислить энергию, излучаемую с поверхности S = 1 м² абсолютно черного тела при температуре Т =1000 К за время t =1 мин. (3,4 МДж)

4.5.19. На какую длину волны приходится максимум спектральной плотности излучательности (энергетической светимости) абсолютно черного тела, имеющего температуру, равную температуре человеческого тела, т.е. t = 37° С? (9,3 мкм)

4.5.20. Солнечные лучи приносят на S =1 м² поверхности почвы энергию Е = 41,9 кДж в минуту. Какова должна быть температура почвы, чтобы она излучала такое же количество энергии обратно в мировое пространство? (60°С)

* Энергетическая светимость – это величина, равная энергии, излучаемой в единицу времени с единицы площади. Эта величина называется также излучательностью тела, интегральной светимостью или суммарной лучеиспускательной способностью.

4.5.21. Максимум энергии излучения абсолютно черного тела приходится на длину волны l₀ = 460 нм. Определить мощность излучения с площади S = 10 см² поверхности этого тела. (89,5 кВт)

4.5.22. Сколько энергии излучается в пространство за Dt =10 ч с площади S=1 га пахотной земли, имеющей температуру t=10°С? Какова масса этого излучения? Считать почву за абсолютно черное тело. (131 ГДж; 1,46 мг)

4.5.23. Принимая Солнце за абсолютно черное тело, определить температуру его поверхности, если длина волны, на которую приходится максимум энергии изложения, l₀ = 0,5 мкм. (5800 К)

4.5.24. Максимум энергии излучения абсолютно черного тела приходится на длину волны l₀=1 мкм. На какую длину волны он сместится, если температура тела уменьшится на DT = 900К? (1,45 мкм)

4.5.25. Суммарная мощность излучения Солнца N = 4×10²⁶ Вт. Определить массу света, излучаемого Солнцем за время Dt =1 с. (4,44×10⁹ кг)

4.5.26. Энергия, приносимая солнечными лучами на Землю в течение года, W=5,6×10²⁴ Дж. На сколько изменилась бы масса Земли за год, если бы она не излучала энергию в пространство? (6.22×10⁴ т)

Модуль 5.

Будова атома. Атомне ядро. Радіоактивність.