Задачи динамики для свободной и несвободной мате­риальной точки

Динамика

Динамика точки. Основные понятия и определения.

В разделе кинематики исследовалось движение тел без учета причин, обеспечивающих это движение. Рассматривалось движение, заданное каким-либо способом и определялись траектории, скорости и ускорения точек этого тела.

В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.

Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.

Понятие о силе, как о величине, характеризующей меру механи­ческого взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоян­ными. Между тем, на движущееся тело наряду с постоян­ными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются.

Как показывает опыт, переменные силы могут определенным об­разом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при посте­пенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопро­тивления среды (воды, воздуха).

К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.

Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одина­ковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.

Количественной мерой инертности данного тела является фи­зическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

В общем случае движение тела зависит не только от его суммар­ной массы и приложенных сил; характер движения может еще зави­сеть от формы тела, точнее от взаимного расположения образующих его частиц (т. е. от распределения масс).

Чтобы при первоначальном изучении динамики иметь возможность отвлечься от учета влияния формы тел (распределения масс), вво­дится понятие о материальной точке.

Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь.

Материальными точками можно считать частицы, на кото­рые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик.

Точку будем называть изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется. Конечно, трудно привести пример подобного состояния. Но представить такое можно.

Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково.

Законы динамики

В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.

Первый закон (закон инерции), открытый Галилеем, гласит: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямо­линейного движения до тех пор, пока приложенные силы не за­ставят ее изменить это состояние. Движение, совершаемое точ­кой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи - пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=0, то точка покоится или движется с постоян­ной по модулю и направлению скоростью ( 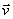=const); ускорение точки при этом равно нулю: 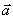= 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.

Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). По данным опыта для нашей Сол­нечной системы инерциальной является система отсчета, начало кото­рой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.

Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

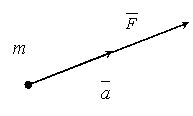
Математически этот закон выражается векторным равенством .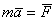

При этом между модулями ускорения и силы имеет место зависимость ma = F.

Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непо­средственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса кото­рой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.

Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействую­щей 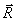, равной геометрической сумме этих сил. Уравнение, выражаю­щее основной закон динамики, принимает в этом случае вид

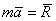или .

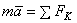Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между мате­риальными телами. Для двух материальных точек он гласит: две ма­териальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

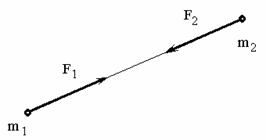
Заметим, что силы взаимодействия между свободными материаль­ными точками (или телами), как приложенные к разным объектам, не образуют уравновешенной системы.

Проведём небольшой эксперимент. Попробуем перемещать тяжёлое тело по некоторой криволинейной траектории. Сразу обнаружим, что тело сопротивляется изменению направления движения, изменению скорости. Возникает сила со стороны тела, противодействующая силе 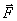, той, которую мы прикладываем к нему.

Эту силу, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки - 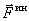. По третьему закону она равна и противоположна действующей на точку силе 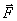, 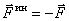. Но на основании второй аксиомы 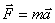. Поэтому .

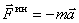Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение

.

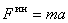И направлена эта сила инерции в сторону противоположную вектору ускорения.

Например, при движении точки по кривой линии ускорение 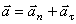. Поэтому сила инерции

.

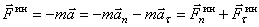То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.

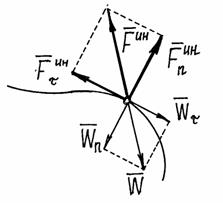
Рис.1

Причём

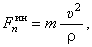
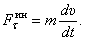
Необходимо заметить, что сила инерции материальной точки, как сила противодействия, приложена не к точке, а к тому телу, которое изменяет её движение. Это очень важно помнить.

Третий закон динамики, как устанавливающий характер взаимодей­ствия материальных частиц, играет большую роль в динамике системы.

Четвертый закон (закон независимого действия сил).При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

;

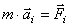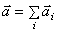
Задачи динамики для свободной и несвободной мате­риальной точки.

Для свободной материальной точки задачами дина­мики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная дей­ствующие на точку силы, определить закон движения точки (вторая или основная задача динамики).

Решаются обе эти задачи с помощью уравнений, вы­ражающих основной закон динамики, так как эти уравнения связывают ускорение 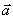т.е. величину, характеризующую движение точки, и действующие на нее силы.

В технике часто приходится сталкиваться с изучением несвобод­ного движения точки, т.е. со случаями, когда точка, благодаря на­ложенным на нее связям, вынуждена двигаться по заданной неподвиж­ной поверхности или кривой.

Несвободной материальной точкой называется точка, свобода движения которой ограничена.

Тела, ограничивающие свободу движения точки, называются связями.

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, которое называется уравнением связи.

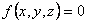
Если точка вынуждена двигаться по некоторой линии, то уравнениями связи являются уравнения этой лини.

,

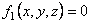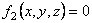
Таким образом, движение несвободной материальной точки зависит не только от приложенных к ней активных сил и начальных условий, но так же от имеющихся связей. При этом значения начальных параметров должны удовлетворять уравнениям связей.

Связи бывают двухсторонние или удерживающие и односторонние или неудерживающие.

Связь называется двухсторонней если, накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве на которых должна находится точка.

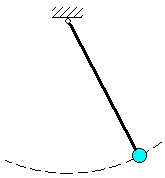
Пример. Материальная точка подвешена на стержне длины .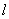

Уравнение связи имеет вид:

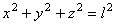
Связь называется односторонней если, накладываемые ею на координаты точки ограничения выражаются в форме неравенств. Односторонняя связь препятствует перемещению точки лишь в одном направлении и допускает ее перемещение в других направлениях.

Пример. Материальная точка подвешена на нити длины .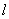

Уравнение связи имеет вид:

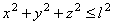
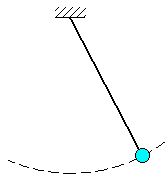
В случаях несвободного движения точки, как и в статике, будем при решении задач исхо­дить из аксиомы связей (принцип освобождаемости от связей), согласно которой всякую несвободную ма­териальную точку можно рассматривать как свободную, отбросив связь и заменив ее действие реакцией этой связи 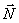. Тогда основной закон динамики для несвободного движения точки примет вид:

,

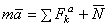где 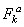-действующие на точку активные силы.

Пусть на точку действует несколько сил. Составим для неё основное уравнение динамики: 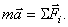Перенесём все члены в одну сторону уравнения и запишем так: 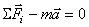или .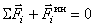

Это уравнение напоминает условие равновесия сходящихся сил. Поэтому можно сделать вывод, что, если к движущейся материальной точке приложить её силу инерции, то точка будет находиться в равновесии. (Вспомним, что на самом деле сила инерции не приложена к материальной точке и точка не находится в равновесии.) Отсюда следует метод решения таких задач, который называется методом кинетостатики:

Если к силам, действующим на точку, добавить ее силу инерции, то задачу можно решать методами статики, составлением уравнений равновесия.

Первая задача динамики для несвободного движения будет обычно сводиться к тому, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи.

Пример 1. При движении автомобиля с постоянным ускорением 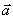, маятник (материальная точка подвешенная на нити) отклоняется от вертикали на угол 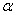(рис.2). Определим с каким ускорением движется автомобиль и натяжение нити.

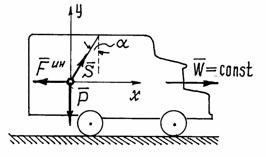
Рис.2

Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.

На точку действуют силы: вес 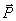и натяжение нити 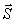, реакция нити. Приложим к точке ее силу инерции 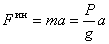, направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:

Рис. 13.1.

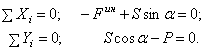
Из второго уравнения следует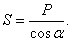

Из первого 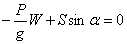и .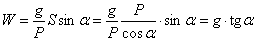

Пример 2.Лифт весом Р (рис.3) начинает подниматься с ускоре­нием 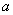. Определить натяжение троса.

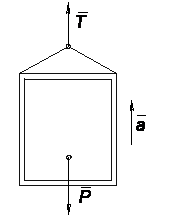
Рис. 3

Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение 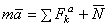в проекции на вертикаль, получаем:

.

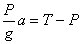Отсюда находим: .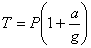

Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:

.
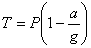