Выражение мощности в комплексной форме

Пусть на входе некоторого двухполюсника известны комплексные изображения напряжения и тока:

; .

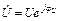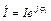Мощность в комплексной форме выражается в виде произведения:

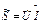, 69(2.59)

где 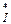– сопряженный комплекс тока.

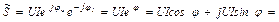
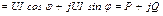. 70(2.60)

2.12. Передача энергии от активного
двухполюсника к пассивному

При работе любой электрической цепи должен иметь место баланс мощностей, т.е. алгебраические суммы активных и реактивных мощностей, развиваемых генераторами, должны равняться алгебраическим суммам активных и реактивных мощностей, поступающих во все пассивные элементы цепи, включая и внутренние сопротивление генераторов.

Полная мощность, развиваемая генератором:

.

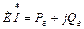Полная мощность, поступающая в любой приемник:

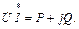
Тогда уравнение баланса мощностей:

71 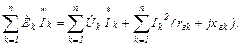, блн (2.61)

где r_гk и x_гk – соответственно внутренние активные и реактивные сопротивления генераторов.

Пусть в электрической цепи работает один источник энергии. Оценим условия, при которых в нагрузке будет выделяться максимальная мощность. Ток в цепи:

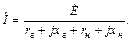
Реактивное сопротивление цепи должно равняться нулю

x_г + x_н = 0,

т.е. цепь должна работать в резонансном режиме, следовательно x_г и x_н должны быть равными по величине и противоположными по характеру (индуктивное и емкостное сопротивления). В итоге:

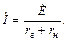
Найдем соотношение между r_г и r_н. Определим мощность приемника:

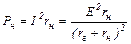
и полагая, что сопротивление нагрузки r_н переменно, исследуем функцию P_н на экстремум:

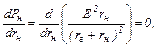откуда

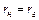72(2.62)

Следовательно, для получения максимальной мощности в нагрузке необходимо, чтобы:

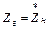. 73(2.63)

Режим работы цепи при этом условии называется согласованным режимом. КПД источника при этом условии:

.

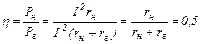При таком низком КПД согласованный режим работы используется только в слаботочных цепях, таких как телефонные линии, линии автоматики и телемеханики, где важна величина полезного сигнала по сравнению с помехами.

Коэффициент мощности

Наибольшие действующие значения напряжения и тока, допускаемые для генераторов и трансформаторов, производящих и, соответственно, преобразующих электрическую энергию, зависят от их конструкции, а наибольшая мощность, которую они могут развивать, не подвергаясь опасности быть поврежденными, определяется произведением этих значений. Поэтому рациональное использование электрических машин и трансформаторов может быть достигнуто лишь в том случае, когда приемники электрической энергии обладают высоким коэффициентом мощности cosφ.

Обычно реактивный ток потребителей энергии носит индуктивный характер, т.е. φ > 0, т.к. наиболее широко используемые асинхронные двигатели потребляют из сети реактивный (индуктивный) ток для создания магнитного поля в машине.

Для улучшения (увеличения) cosφ группы приемников параллельно им включают конденсаторы.

Покажем, как рассчитать емкость, необходимую для повышения cosφ.

Пусть суммарная активная мощность приемников:

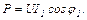
При увеличении cosφ и неизменном напряжении сети:

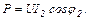
Следовательно, I₂ < I₁.

Проиллюстрируем расчет необходимой величины емкости для повышения коэффициента мощности до значения cosφ₁ с помощью векторной диаграммы.

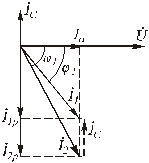
Рис.2.33. Векторная диаграмма, иллюстрирующая
повышение коэффициента мощности

Рассчитаем необходимый емкостной ток.

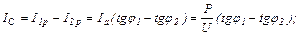
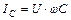, отсюда:

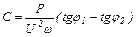. 74(2.64)

Такую же роль, как конденсаторы, могут играть синхронные двигатели, работающие в «перевозбужденном» режиме. Они при этом потребляют из сети ток, реактивная составляющая которого носит емкостной характер.