Тема: «Геометрия: объем, площадь поверхности». Часть 7 . Тела вращения
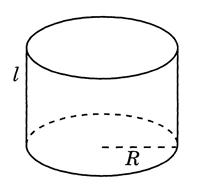
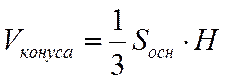 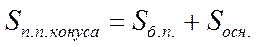 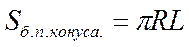 , , 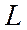 -образующая -образующая |    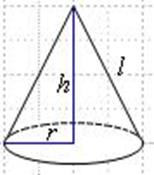 | |
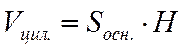 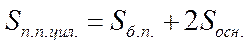 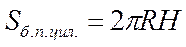 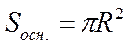 |   | |
  |  | |
1. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2. Во сколько раз объём первого цилиндра больше объёма второго?
2. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
| 3. Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой? | 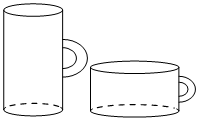 | |
| 4. Даны две кружки цилиндрической формы. Первая кружка в четыре раза ниже второй, а вторая в полтора раза шире первой. Во сколько раз объём первой кружки меньше объёма второй? | 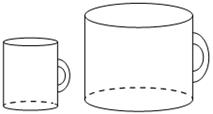 | |
| 5. Даны два конуса. Радиус основания и высота первого конуса равны соответственно 4 и 9, а второго — 6 и 8. Во сколько раз объём второго конуса больше объёма первого? | ||
| 6. Объём конуса равен 60π, а его высота равна 5. Найдите радиус основания конуса. 7. Объём конуса равен 9π, а радиус его основания равен 3. Найдите высоту конуса. | 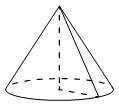 | |
| 8. Объём конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью. 9. Объём конуса равен 250. Через точку, делящую высоту конуса в отношении 1:4, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью. | 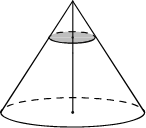 | |
| 10. Объём конуса равен 9π, а радиус его основания равен 3. Найдите высоту конуса. |  | |
| 11. Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у данного? Ответ дайте в сантиметрах. | 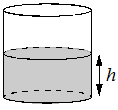 | |
| 12. Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего? 13. Даны два шара с радиусами 6 и 2. Во сколько раз объём большего шара больше объёма меньшего? |  | |
14. Высота бака цилиндрической формы равна 60 см, а площадь его основания 150 квадратных сантиметров. Чему равен объём этого бака (в литрах)? В одном литре 1000 кубических сантиметров.
15. В бак, имеющий форму цилиндра, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,2 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
| 16. В сосуде, имеющем форму конуса, уровень жидкости достигает 12 высоты. Объём жидкости равен 90 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху? | 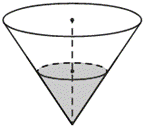 |
Домашнее задание:
1. Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 8, а второго — 12 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
2. Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 1, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
3. Даны два шара с радиусами 8 и 2. Во сколько раз объём большего шара больше объёма другого?
| 4. Объём конуса равен 135. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью. |  |
| 5. Вода в сосуде цилиндрической формы находится на уровне h= 60 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах. | 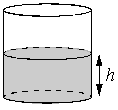 |
