Сферические волны

Такой волновой тип получается в случаях, когда точечный источник возбуждает однородное неограниченное пространство. Простейший случай, в котором только от радиальной координаты r зависит амплитуда колебания:

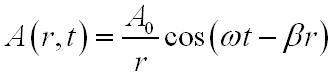
или же, если сформулировать величину A (r,t) через её комплексную амплитуду

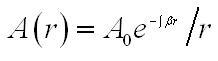
Цилиндрические волны

Источник — бесконечные нити. При этом волновые фронты обладают видом концентрических цилиндров. На расстоянии от оси значительно превышающем длину волны справедливо следующее приближенное равенство:

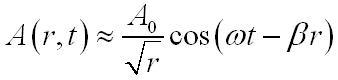
Однородная плоская эл/м волна с линейной поляризацией

Относительно рассматриваемой плоской волны приведём следующие предположения:

а)ориентирован вдоль оси z комплексный вектор Пойнтинга причем единственная составляющая вещественна:

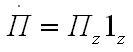
откуда следует, что продольные составляющие магнитного и электрического полей в рассматриваемой плоской волне равны нулю:

E_z=0 H_z=0

б) плоская волна однородна, то есть вдоль волнового фронта амплитуды полей неизменны; от того, что все волновые фронты полностью параллельны плоскости XOY, крайнее условие записывается математически следующим образом:

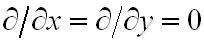
в)из возможных двух поперечных составляющих электрического вектора E`<sub>x</sub> и E`_y лишь E`_x отлична от нуля. Тем самым, в плоскости XOY колеблется электрический вектор. Плоскость эта именована плоскостью поляризации, а сама волна – плоской волной с линейной поляризацией. Система уравнений Гельмгольца

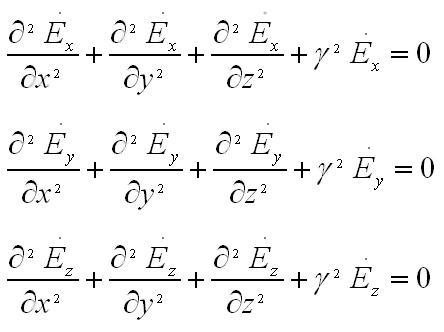
с учетом сделанных предположений, сравнительно составляющих электрического вектора обращается в единственное уравнение

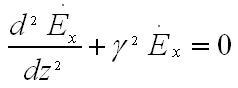
Знак частной производной в этом уравнении сменен на знак обыкновенной производной, потому что неизвестная функция зависит лишь от координаты z. Решение представленного уравнения в общем положении имеет следующий вид:

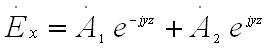
Где A`<sub>1</sub> и A`₂, - произвольные, вообще говоря, комплексные, постоянные. Положим для определенности A`₂=0 , тогда

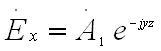
Определим магнитный вектор в данной плоской волне

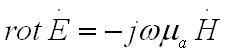
откуда следует

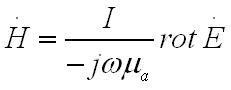
Раскрыв операцию rot, убеждаемся, что

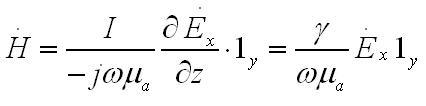
В итоге, вектор магнитного поля представленной плоской волне располагает лишь составляющей H`y, таким образом, перпендикулярен к вектору электрического поля. Крайне важно отметить, что, между составляющими как это следует из

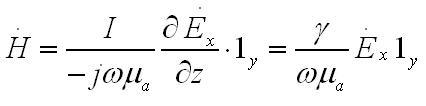
магнитного и электрического полей имеется пропорциональность:

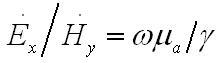
Вывод отсюда состоит в следующем, при отсутствии потерь в среде, то есть при γ вещественном, поля E` и H` колеблются в фазе. Это означает, в соответствии с

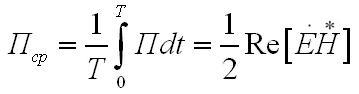
что плоская электромагнитная волна в среде переносит без потерь только активную мощность.

Zc - некоторая постоянная, которая имеет размерность сопротивления и называется характеристическим (волновым) сопротивлением данной среды.

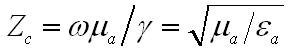
Плоские эл/м волны в хорошо проводящих средах

Не забыть σ в формулах,написана очень мелко

Рассмотрим распространении плоских волн в металлоподобных средах и реальных металлах. С электродинамической точки зрения по определению среда приходится хорошо проводящей, то есть металлоподобной, если же в каждой из её точек плотность токов проводимости

>>

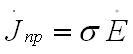
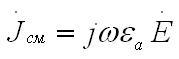
Такое же условие металлоподобности может быть выражено и как

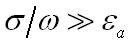
Вполне явственно, что чем ниже частота ω, тем скорее ближе среда приближается к идеальному металлу.

Комплексную диэлектрическую проницаемость металлоподобной среды соответственно сделанному предположению можно считать мнимой:

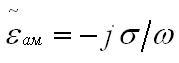Найдем в такой среде комплексную постоянную распространения плоских электромагнитных волн. По общему правилу,

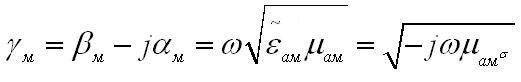Поскольку

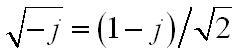
можно переписать в виде

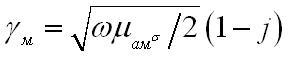Итак,

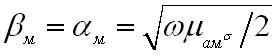
Здесь довольно просто можно определить длину волны в хорошо проводящей среде:

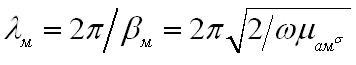
В металле длина волны существенно сокращается по отношению с длиной волны в свободном пространстве

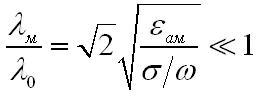
Граничные условия для векторов электрического поля

тангенсальные составляющие

Для контура изображенного ниже в соответствии с этим законом,

будем иметь

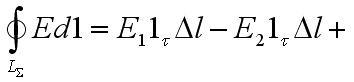
+ циркуляция по боковым сторонам. Это все равно

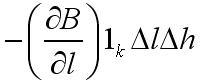
Функция

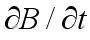стоящая в правой части этого состава является величиной конечной для любых граничащих сред, отчего предельный переход при

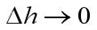
дает

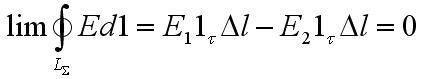
откуда

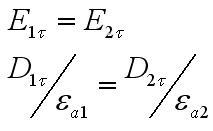
Тем самым, на границе раздела сред тангенциальные составляющие векторов напряженности электрического поля непрерывны.

Проанализируем в отдельности граничные условия в том случае, когда средой 2 на изображении выше является безупречный металл. Как уже известно, здесь, всегда E₂=0

Значит для идеального проводника граничное условие принимает вид Eτ=0

Силовые линии электрического поля в соответствии с этим условием должны подходить по направлению нормали к поверхности безупречного металла.

Нормальные составляющие

Для электрического поля divD=ρ

Тут возможны два случая:

1. Плотность электрических поверхностных зарядов равна нулю. Заключенный внутри малой цилиндрической области суммарный электрический заряд равен нулю.

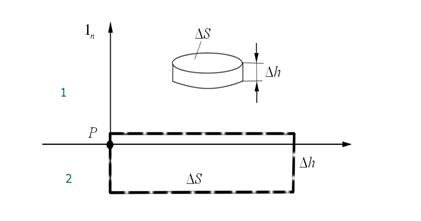
В соответствии с теоремой Гаусса

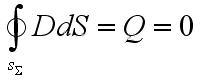
откуда следует D_1n=D_2n и

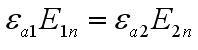
Следовательно, в отсутствии поверхностных электрических зарядов на границе раздела двух сред, нормальные составляющие векторов электрического смещения непрерывны, в тот момент как в общем случае нормальные составляющие напряженностей электрического поля претерпевают скачок.

2. Равномерно распределен на границе раздела поверхностный электрический заряд с плотностью

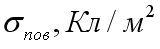
В таком случае, явно не влияет на величину заряда стремление к нулю высоты цилиндра ∆h, заключенного внутри области. Можно записать формулу, воспользовавшись законом Гаусса,

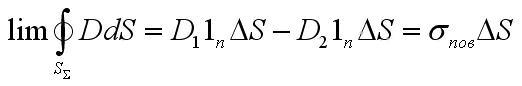
откуда

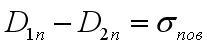
Согласно изображению выражения выше следует, что нормальные составляющие векторов электрического смещения при наличии заряженной границы раздела испытывают скачок на величину плотности поверхностного заряда в исследуемой точке. Это обусловлено физически тем, что расположенный на поверхности заряд формирует собственное поле, ориентированное так, что от границы раздела по одну сторону это поле складывается с внешним полем, а по другую вычитается.

Граничные условия для векторов магнитного поля

тангенциальные составляющие

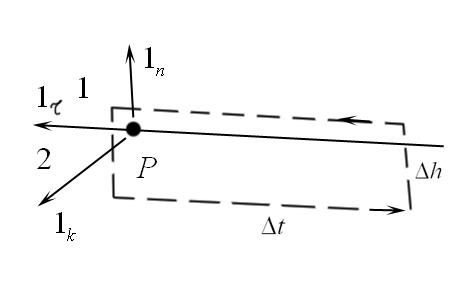
Три взаимно ортогональных единичных вектора lτ,ln,l_k введем в точке P. 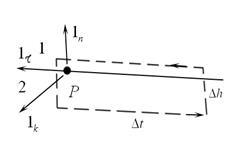Единичными векторами нормального и тангенциального направлений по-прежнему являются два из них, а вектор l_k создаст нормаль к плоскости, образованной двумя первыми векторами и лежит в плоскости границы раздела. В окрестности точки Р со сторонами ∆l и ∆h (∆h<<∆l)

выделим достаточно малый прямоугольный контур лежащий в плоскости, образованной векторами lτ и ln. Будем полагать, что задано такое направление обхода на контуре, которое наблюдается с конца вектора l_k против часовой стрелки. К контуру используем закон полного тока, будем полагать, что достаточно малы размеры сторон контура для того, чтобы считать в их пределах векторы поля Н постоянными. В итоге получим:

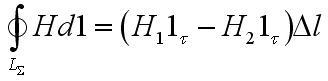
На данном этапе нужно разобрать два случая:

1. Величинами конечными являются электродинамические параметры обеих граничащих сред. Здесь же непосредственно вытекает конечное значение векторов плотности токов проводимости и смещения. Произведем предельный переход, направляя высоту контура ∆h к нулю. При этом будет равна нулю также величина циркуляции вектора Н. Будем иметь:

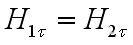
Тем самым, непрерывны тангенциальные составляющие векторов напряженности магнитного поля в конечных значениях электродинамических параметров сред. Вот тут следует, что терпят разрыв тангенциальные составляющие векторов магнитной индукции:

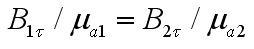
2. Бесконечна проводимость одной из граничащих сред. Ток проводимости будет протекать по тонкой пленке и lim правой части не равен 0. В целях характеристики токов, протекающих по поверхности безупречного проводника, вводят представление вектора плотности поверхностного тока η.

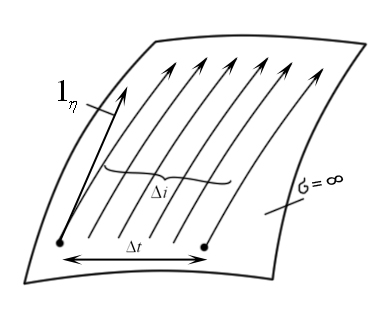
Для начала, проводится касательный к линиям тока в данной точке единичный вектор, который обозначается через ln. Далее находится величина тока ∆i, проходящего через отрезок ∆l, перпендикулярный вектору ln. Затем определяется плотность поверхностного тока как

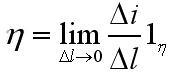
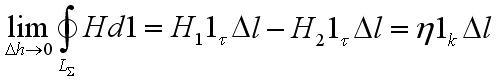
Следом необходимо учесть, что внутри безупречного проводника должны равняться нулю все составляющие электромагнитного поля. Отчего H₂=0, получим

H₁lτ=ηl_k

С тем учетом, что

lτ=-[l_n l_k]

можно записать

η=[l_n H₁]

Тем самым, на границе раздела с идеальным металлом поверхностный ток протекает в направлении, перпендикулярном вектору H₁, а также численно равен напряженности магнитного поля.

Векторный и скалярный потенциалы эл/м поля

Обычно, если рассматриваемые задачи со сторонними источниками, используют искусственный прием - вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. А соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля. Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:

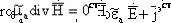Существует следующее векторное тождество:

B=rot A

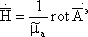
(5)

Векторную функцию A называют векторным электрическимпотенциалом. Соотношение (5) при известном A однозначно определяет вектор H. Обратное определение неоднозначно, т.е. при известном векторном поле H соотношение (5) определяет A неоднозначно. Известно, что rot grad =0. Поэтому, если ввести A и A=A+frad U, то соотношение (5) не изменится. Поэтому соотношение (5) определяет A с точностью до градиента произвольной функции.

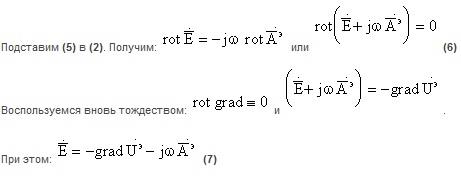Скалярную функцию U называют скалярным электрическим потенциалом. Знак " - " поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал.