Плоские и сферические волны

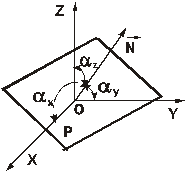Плоские волны. Предположим, что источник волн представляет собой бесконечную, равномерно заряженную плоскость , заряд на которой меняется с частотой . Из соображений симметрии ясно, что все возмущения от этой плоскости будут распространяться в направлении нормали к ней, т.е. в каждый момент времени поле будет изменяться в направлении нормали и оставаться неизменным в плоскостях, перпендикулярных ей. Выберем систему координат так, что бы начало ее находилось в плоскости , а вектор нормали к ней 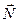составлял углы 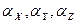с соответствующими осями координат. Таким образом, вектор 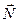является единичным и его компоненты имеют вид

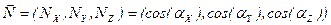. (3.1)

Условием постоянства поля в плоскостях, параллельных 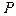, является то, что аргументы решения волнового уравнения должны быть связаны условием, что они удовлетворяют уравнениям этих плоскостей, т.е. переменные 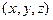в волновом уравнении должны быть в комбинации

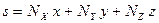(3.2)

т.е. 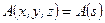. Перейдем в уравнении (2.13) (представленном в координатах)

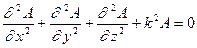(3.3)

к переменной 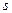(3.2).

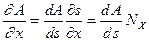;	(3.4а)
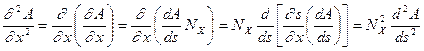.	(3.4б)

Выполняя аналогичные действия для производных по 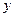и и 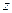подставляя полученные выражения в (3.3). получим

,

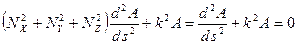(3.5)

где 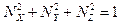, т.к. 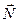- единичный вектор.

Получилось обыкновенное дифференциальное уравнение второго порядка, решение которого хорошо известно

.

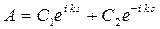(3.6)

Так как нас интересует лишь уходящая волна, то 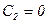и решение можно записать в виде (полагая )

,

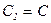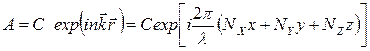(3.7)

где 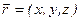, 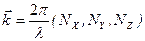- т.н. волновой вектор, длина которого равна волновому числу, а направление совпадает с направлением распространения волны. Выражение (3.7) представляет собой уравнение плоской волны, выраженное через комплексную амплитуду.

Объединяя компоненты 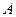в вектор (т.к. у каждой компоненты будет такое же выражение для волны ), можно записать

,

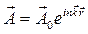(3.8)

где 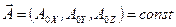- амплитуды компонент. Возвращаясь к временной зависимости, найдем, что напряженность магнитного поля

,

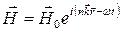(3.9)

где 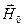вектор амплитуд напряженности магнитного поля.

Соотношения между векторами напряженности электрического и магнитного поля. Так как уравнения Максвелла в однородном изотропном пространстве без токов и зарядов симметричны относительно 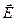и 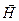, то, выполняя аналогичные действия для 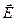, можно получить выражение для плоской волны электрического поля

,

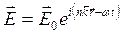(3.10)

где 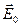вектор амплитуд напряженности электрического поля.

Найдем зависимость между 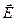и 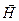в плоской волне. Для этого подставим выражение (3.9) в первое уравнение Максвелла (1.1)

.

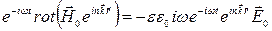(3.11)

Воспользовавшись формулой векторного анализа

,

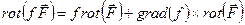(3.12)

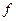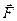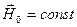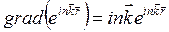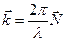где - скалярная, а - векторная функция и учитывая, что , и , получим

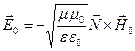. (3.13)

По аналогии, подставляя (3.10) в (1.2) получим

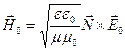. (3.14)

Выражения (3.13) и (3.14) показывают, что векторы 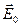и 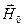перпендикулярны вектору .

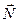Умножая (3.13) скалярно на 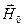и учитывая, что 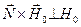, получим, что

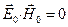, (3.15)

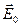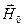т.е. и перпендикулярны друг другу. Таким образом, векторы 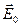, 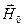и 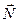образуют тройку взаимно перпендикулярных векторов, откуда следует, что электромагнитные волны поперечны.

Вычисляя модуль выражения (3.13) или (3.14), найдем связь между ,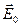

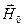
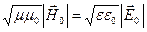. (3.16)

Наконец, умножая (3.14) справа векторно на 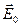, и раскрывая двойное векторное произведение по формуле 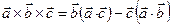, а также учитывая, что 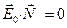, получим, что

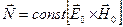, (3.16)

т.е. векторы 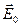, 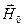и 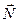образуют правую тройку и направление распространения волны можно определить по правилу “буравчика”.

Подобным образом ведет себя волна всякой формы, так как на малых площадках волну любой формы можно считать плоской, если .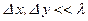

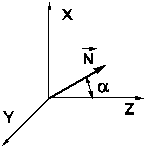Наклонная волна. Существует очень важный частный случай плоской волны - наклонная волна, которой называется волна, распространяющаяся под малым углом 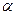к некоторому заданному направлению. Определим систему координат так, что бы ось 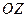совпадала с этим направлением, а вектор 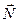располагался в плоскости 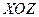. Тогда

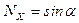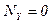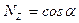, , . (3.17)

Считая угол 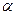малым, можно считать 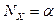, и

(это параксиальное приближение). Окончательно, уравнение наклонной волны будет

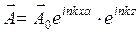. (3.18)

Поляризация волн. Возвращаясь к уравнению для плоских волн, распространяющихся вдоль оси 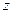, вспомним, что оно векторное и решения для компонент 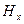и 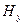( 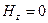) имеют одинаковый вид, отличаясь лишь постоянными интегрирования

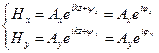(3.19)

Таким образом плоскую, а следовательно и любую волну ( которая всегда представима плоской на малой площадке ) можно считать суммой двух взаимно перпендикулярных колебаний со сдвигом фаз 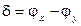. Переходя к действительным переменным, запишем зависимость таких колебаний от времени

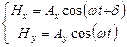(8.5)

Это выражение представляет собой параметрическое уравнение кривой, которую описывает проекция конца вектора 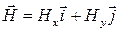на координатную плоскость 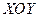, при этом волна распространяется вдоль оси 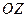с постоянной скоростью. Для получения явного выражения для этой кривой, необходимо из (8.5) исключить параметр 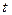, чего проще всего достичь следующим образом:

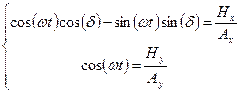или

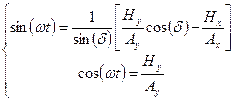Возводя в квадрат оба уравнения и складывая их, после преобразований получим

.

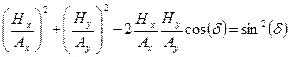(8.6)

рис 8.1

рис 8.2

Полученное выражение представляет собой в общем случае уравнение эллипса относительно координат 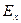и 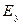, а траектория конца вектора 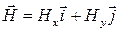представляет собой спираль, “намотанную” на эллиптический цилиндр, опирающийся на этот эллипс.

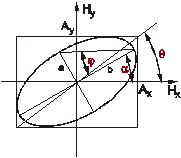
В общем случае график (8.6) имеет вид, показанный на рисунке. Из теории кривых второго порядка известно:

1. Эллипс вписан в прямоугольник со сторонами 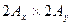, которые связаны с полуосям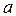и и 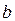соотношением

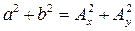; (8.7)

2. Углы, характеризующие эллипс связаны зависимостями

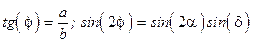; (8.8)

3. Угол 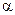, определяющий ориентацию эллипса связан с 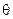, как

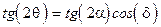. (8.9)

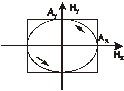
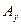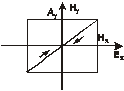
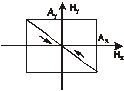
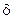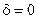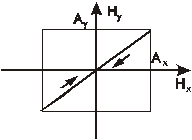
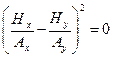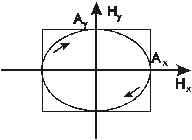
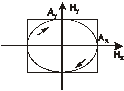
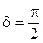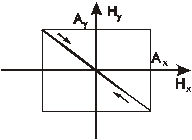
При различных соотношениях между , и возможны различные формы и ориентации эллипса. В частности, если , то выражение (8.6) представляет собой квадрат разности , а кривая вырождается в линию, которую можно считать частным случаем эллипса (рис 8.3), при этом мы имеем случай линейной поляризации. Если , то (8.6) представляет собой эллипс, с полуосями параллельными осям координат (рис 8.4) (каноническое уравнение эллипса), а если 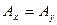, то эллипс превращается в окружность (это случай круговой поляризации). При 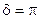получается опять линейная поляризация 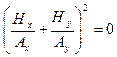(рис 8.5) .

рис 8.4	рис 8.5	рис 8.6

Направление вращения вектора можно определить из (8.5), находя 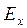и 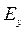при изменении времени 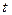. При этом различают правую поляризацию, если в направлении движения волны вектор вращается по часовой стрелке, и левую, если наоборот.

1.		2.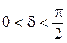
3.		4.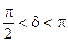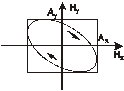
5.	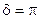	6.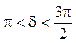
7.		8.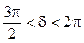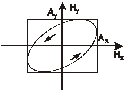

Эллиптические колебания можно рассматривать как общий случай поляризации. В предельных случаях, в зависимости от амплитуды и разности фаз, эллипс вырождается в прямую линию или окружность. Зависимость формы и ориентации эллипса от фазы 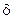приведена в таблице.

Приведенные выше соотношения относятся к плоской монохроматической волне, вышедшей из точечного источника. В природе, помимо оптических квантовых генераторов, все источники света состоят из огромного числа независимых друг от друга источников, при этом каждый из них испускает свет порциями (цугами) продолжительностью порядка 10^-8 сек. (об этом позже ). В этом случае поляризации все лучей смешиваются случайным образом и все поляризационные эффекты усредняются. Такой свет называется естественным или неполяризованным, у него возникает осевая симметрия вектора поляризации. Можно считать, что естественный свет представляет собой сумму двух независимых линейно поляризованных волн одинаковой интенсивности с взаимно перпендикулярными поляризациями, или двух независимых волн одинаковой интенсивности с круговой поляризацией, у которых векторы вращаются в разные стороны.

Сферическая волна. Источником сферической волны может быть либо точка, либо равномерно заряженная сфера. В этом случае волновой фронт имеет сферическую форму, концентричную с источником. Если поместить начало координат в центр источника, то в силу симметрии относительно центра, во первых - ориентация осей системы координат будет безразличным, а во вторых - характеристики электромагнитного поля будут постоянными на сферах, концентричных центру. Второе означает, что переменные 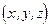в уравнении могут быть лишь в комбинации

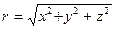. (4.1)

Это означает, что переменные удовлетворяют уравнениям сфер, концентричных центру.

Переходя в (3.3) к переменной , получим

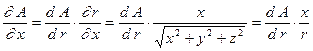
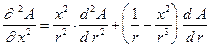. (4.2)

Выполняя аналогичные преобразования с производными по переменным 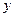и и 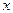подставляя их в уравнение (3.3), получим

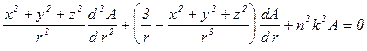, (4.3а)

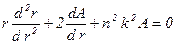. (4.3б)

Вводя новую функцию 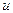соотношением 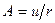, это уравнение можно привести к линейному дифференциальному уравнению с постоянными коэффициентами

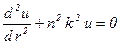, (4.4)

решение которого хорошо известно

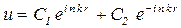. (4.5)

По аналогии с плоской волной будем считать 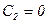и 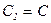, т.е.

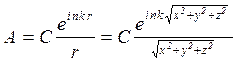. (4.6)

Полученное выражение есть уравнение сферической волны.