Пример 1. Исходные данные приведены в таблице 1.

Табл.1

ПН ПО	B1	B2	B3	B4	B5	Запасы ai
A1
A2
A3
A4
Заявки bj

Заполняем таблицу постепенно, с левой верхней ячейки (1,1) («северо-западного угла» таблицы). Пункт B₁ подал заявку на 200 ед. груза. Удовлетворим эту заявку за счет запаса 100, имеющегося в пункте A₁, и запишем перевозку 100 в клетке (1,1). Запасы 1-го поставщика полностью израсходованы, поэтому остальные клетки 1-ой строки прочеркиваем. Потребности пункта B₁ остались неудовлетворенными на 200-100=100 ед. Сравниваем этот остаток с запасами поставщика A₂: т.к. 100<200, то 100 ед. записываем в клетку (2,1), чем полностью удовлетворяем потребности потребителя В₁, а оставшиеся клетки 1-го столбца прочеркиваем.

У поставщика А₂ осталось еще 150 единиц груза. Удовлетворим за счет них заявку пункта B₂ (200 единиц). Для этого сравниваем этот остаток с потребностями потребителя В₂: 150<200, записываем 150 ед. в клетку (2,2) и, т.к. Запасы А₂ полностью израсходованы, поэтому остальные клетки 2-ой строки прочеркиваем. Потребности B₂ остались неудовлетворенными на 50 единиц. Удовлетворим их за счет поставщика А№, и т.д. Процесс продолжаем до тех пор, пока не удовлетворим всех потребителей за счет запасов поставщиков. (см. табл. 2).

Таблица 2.

ПН ПО	B1	B2	B3	B4	B5	Запасы ai
A1		-	-	-	-
A2			-	-	-
A3	-				-
A4	-	-	-
Заявки bj

Нами составлен план перевозок, удовлетворяющий балансовым условиям: Х=(х₁₁=100; x₂₁=100_; x₂₂=150; x₃₂=50; x₃₃=100; x₃₄=50; x₄₄=50; x₄₅=250), остальные значения переменных равны 0.

Более наглядно изобразить рассматриваемый план в виде матрицы перевозок: X= 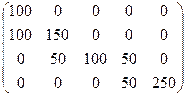Полученное решение является не только допустимым, но и опорным решением ТЗ, т. к., используя метод вычеркивания, мы можем убедиться, что будут вычеркнуты все столбцы и строки, цикл построить нельзя из полученных занятых клеток, и значит вектора условий линейно независимы. В то же время план невырожденный, т.к. содержит r=m+n-1=4+5-1=8 занятых клеток. Остальные клетки - свободные (пустые), их число равно (n - 1) (m - 1) = 12.

Найдем общую стоимость составленного плана как сумму произведений объемов перевозок, стоящих в левом углу занятых клеток, на соответствующие стоимости в этих же клетках: L=100×10+100×2+150×7+50×5+100×3+50×2+50×16+250×13=6950 (ед).

Если в результате заполнения получается план, количество выделенных клеток которого будет меньше, чем m+n-1 (план вырожденный), следует к уже заполненным клеткам присоединить определенным образом выбранную незаполненную клетку, называемую фиктивно занятой, в нее поместить нулевой объем перевозки. Выбор необходимой клетки состоит в возможности построения замкнутого цикла для искомой клетки, все вершины которого лежали бы в занятых клетках.

2.Метод минимальной стоимости.

Данный метод получения опорного плана, при котором учитывается стоимость перевозки единицы груза, позволяет строить план, значительно более близкий к оптимальному.

Заполнение таблицы начинают с клетки, имеющей наименьшую стоимость единицы перевозки. Если таких клеток несколько, то выбирают произвольно любую из имеющихся.

Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого в результате заполнения исчерпываются, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворяются.

Возможны случаи, когда приходится вычеркивать и строку и столбец, на пересечении их будет находиться заполняемая клетка. Это возможно, когда израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимости снова выбираем наименьшую стоимость, и процесс заполнения клеток продолжается, пока не будут распределены запасы поставщиков и удовлетворены потребности потребителей.

Пример 2. Составить начальное опорное решение, используя метод минимальной стоимости. Исходные данные приведены в таблице 3.

Таблица 3.

ПН ПО	B1	B2	B3	B4	B5	Запасы ai
A1	-	-	-		-
A2			-	-	-
A3	-	-	-	-
A4	-			-
Заявки bj

В результате получен план Х=(х₁₄=100; x₂₁=200_; x₂₂=50; x₃₅=200; x₄₂=150; x₄₃=100; x₄₅=50), остальные значения переменных равны 0.

Матрица перевозок: X= 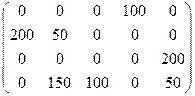. План не содержит циклов и состоит из 7 положительных перевозок, следовательно, является вырожденным опорным планом. Данный опорный план имеет стоимость:

Z=100*1+200*2+50*7+200*2+150*8+100*12+50*13=4300 (ед).

Стоимость этого плана оказалась несколько меньшей стоимости опорного плана, полученного методом северо-западного угла.

7.3. Метод последовательного улучшения плана перевозок,
цикл пересчета

В ТЗ переход от одного опорного плана к другому осуществляется с помощью цикла. Для некоторой свободной клетки таблицы строится цикл, содержащий часть клеток, занятых опорным решением.

Циклом пересчета называется такой цикл в таблице с базисным распределением перевозок, при котором одна из его вершин лежит в свободной клетке, остальные – в занятых.

Цикл пересчета называется означенным, если в его вершинах расставлены знаки “+” и “-“ так, что в свободной клетке стоит знак “+”, а соседние вершины имеют противоположные знаки.

Сдвигом по циклу на некоторую величину g называется увеличение объемов перевозок во всех клетках цикла, отмеченных знаком “+”, и уменьшение объемов перевозок на ту же величину g во всех клетках цикла, отмеченных знаком “-“. По-другому это может называться перенос («переброс») какого-то количества единиц груза g по означенному циклу.

Очевидно, что при переносе любого числа единиц по циклу, равновесие между запасами и заявками не меняется: по-прежнему сумма перевозок в каждой строке равна запасам этой строки, а сумма перевозок в каждом столбце - заявке этого столбца. Таким образом, при любом циклическом переносе, оставляющем перевозки неотрицательными, допустимый план остается допустимым, хотя стоимость плана может изменяться - увеличиваться или уменьшаться.

Теорема. Для каждой свободной клетки транспортной таблицы всегда существует и притом единственный цикл пересчета, одна из вершин которого лежит в этой свободной клетке, а все остальные - в базисных клетках.

При улучшении плана циклическими переносами пользуются приемами, заимствованными из симплекс-метода: при каждом шаге (цикле) заменяют одну свободную переменную на базисную, т.е. заполняют одну свободную клетку и взамен этого освобождают одну из базисных клеток. При этом общее число базисных клеток остается неизменным и равным m + n - 1. Таким образом, по построенному циклу перераспределяются объемы перевозок (осуществляется сдвиг по циклу). Перевозка “загружается” в выбранную клетку и освобождается одна из занятых клеток, получается новый опорный план.

Количество единиц груза g, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки). Если циклов с отрицательной ценой в таблице больше не осталось, это означает, что дальнейшее улучшение плана невозможно, т.е. оптимальный план достигнут.