Предельные точки множества и предел функции

точка 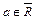называется предельной точкой множества 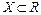, если любая ее окрестность содержит хотя бы одну точку из отличную от а.

Множество всех предельных точек для обозначают 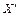, поэтому: .

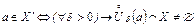Сама предельная точка а может и не быть элементом Х. Слова «любая окрестность» означают, что в произвольной окрестности точки а содержится бесконечное число точек множества Х, из которых можно выделить бесконечную последовательность различных точек 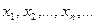сходящуюся к а.

Определение предела функции в точке по Коши. Пусть функция f(x) определена всюду в окрестности точки а, за исключением, быть может, самой точки а:

Û .

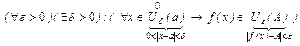Определение предела функции в точке по Гейне. Число А является пределом функции f(x) в точке а, если функция определена в некоторой проколотой d-окрестности точки а и для любой последовательности 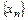значений аргумента, сходящейся к а, соответствующая последовательность значений функции {f(x_n)} сходится к А, т.е:

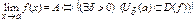Ù .

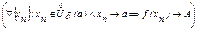Определения предела функции по Коши и Гейне равносильны.

Локальными назовем такиесвойства функции, которые зависят от ее поведения в малых окрестностях рассматриваемой точки. Существование 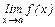и его значение – локальное свойство функции f(x).

Различные типы пределов

Число А₁ называют пределом слева функции f(x) в точке а и обозначают 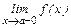= = 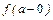А₁, если .

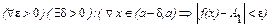аналогично для предела функции справав точке а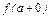: 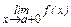=А₂Û.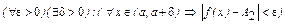

А₁, А₂– односторонние пределы (характеризуют поведение функции в левой (правой) полуокрестности предельной точки.

Определим бесконечные пределы в конечной точке.

Функцияf(x) имеет бесконечный предел 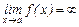, если она определена в некоторой проколотой окрестности точки а и

Для произвольной e-окрестности бесконечно удаленной точки 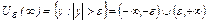найдется проколотая окрестность 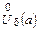точки а, что .

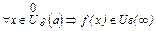Пусть аргумент функции принимает по абсолютной величине сколь угодно большие значения. При этом несобственное число ¥ является предельной точкой множества D(f) и допустимо рассматривать предел на бесконечности: .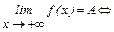

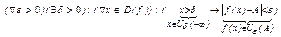Из определения видно, что значения функции при х£d не влияют на величину предела при 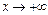. При вычислении 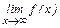рассматривают поведение функции для достаточно больших х.

Поведение функции может изучаться на каком-то подмножестве D(f), поэтому вводится понятие предела по множеству.

Если функция f(x) существует в каждой точке некоторого множества EÍD(f) и а – предельная точка множества E, то число A называют пределом функции f в точке а по множеству E:

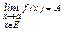Û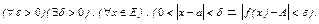

В отличие от прежнего определения из 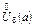берутся только точки множества 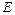. Такой предел называют частичным. Односторонние пределы - разновидности частичных.

Рассмотрим функцию Дирихле Для доказательства того, что 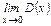не существует, установим связь между пределом по множеству с частичными пределами.

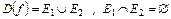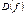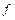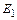Теорема. Пусть область определения функции разбита на два множества и а – предельная точка этих множеств. Для существования предела по всему множеству необходимо и достаточно, чтобы существовали частичные пределы функции по и 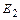, которые были бы равны между собой.