Примеры решения задач на тему «Кривые второго порядка»
Пример 1: Найти координаты фокусов и эксцентриситет эллипса 
Решение: Для данного эллипса  и поэтому
и поэтому

Следовательно, фокусы имеют координаты  и
и  , эксцентриситет
, эксцентриситет 
Пример 2: Найти полуоси, координаты фокусов и эксцентриситет эллипса

Решение: Разделив на 36, приведем данное уравнение к виду

Отсюда следует, что большая полуось эллипса  , а малая полуось
, а малая полуось  . При этом ось эллипса и его фокусы расположены на оси
. При этом ось эллипса и его фокусы расположены на оси  . Найдем
. Найдем  по формуле
по формуле
 .
.
Следовательно, координаты фокусов  и
и  , а его эксцентриситет
, а его эксцентриситет

Пример 3: Составить каноническое уравнение эллипса, зная, что его большая полуось  , а его эксцентриситет
, а его эксцентриситет  . Найти расстояние между фокусами эллипса.
. Найти расстояние между фокусами эллипса.
Решение: Воспользуемся формулой, выражающей эксцентриситет через отношение полуосей:
 , или
, или  , откуда
, откуда  .
.
В данном случае 
Следовательно, каноническое уравнение эллипса
 .
.
Так как  , то
, то  ;
;  и расстояние между фокусами
и расстояние между фокусами 
Пример 4: Асимптоты гиперболы имеют уравнения  , а расстояние между фокусами равно 20. Написать ее каноническое уравнение.
, а расстояние между фокусами равно 20. Написать ее каноническое уравнение.
Решение: Разрешим уравнения асимптот относительно 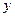 и, сравнив с общей формулой асимптот, найдем отношение
и, сравнив с общей формулой асимптот, найдем отношение 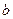 к
к 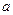 :
:

Кроме того,  , т.е.
, т.е.  . Так как для гиперболы
. Так как для гиперболы  , то для нахождения
, то для нахождения 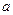 и
и 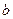 получим систему уравнений
получим систему уравнений

решая которую, найдем  . Следовательно, каноническое уравнение гиперболы имеет вид
. Следовательно, каноническое уравнение гиперболы имеет вид

Пример 5: Парабола с вершиной в начале координат проходит через точку  и симметрична относительно оси
и симметрична относительно оси  . Написать ее уравнение.
. Написать ее уравнение.
 |
Решение: Так как парабола симметрична относительно оси
 и проходит через точку
и проходит через точку  с положительной абсциссой, то она имеет вид, представленный на рис.
с положительной абсциссой, то она имеет вид, представленный на рис. Подставляя координаты точки  в уравнение такой параболы
в уравнение такой параболы  , получим
, получим  , т.е.
, т.е.  .
.
Следовательно, искомое уравнение

фокус этой параболы  , уравнение директрисы
, уравнение директрисы 
