Изучение колебаний физического маятника”

Лабораторная работа №6.

Теоретическое введение:

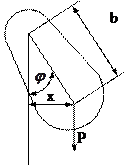Физический маятником называют твердое тело, способное совершать колебания вокруг горизонтальной оси, не проходящей через его центр массы С.

Если на маятник, кроме силы тяжести Р, никакие другие силы не действуют, то в случае малых отклонений от положения равновесия он будет совершать свободные гармонические колебания. Дифференциальное уравнение таких колебаний, при соблюдении указанных выше условий имеет вид:

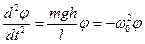(1)

Его решение: 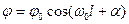(2)

Из (1) и (2) можно найти, что период колебаний физического маятника определяется выражением:

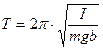(3)

где: m – масса маятника; I – его момент инерции относительно оси О и b – расстояние от оси до центра масс маятника. Так как - малая величина, то величина х пропорциональна 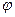и поэтому решение (2) можно записать в другом виде:

х – смещение произвольной точки маятника из положения равновесия.

А – амплитуда колебаний.

Т.к. реально на маятник, кроме силы тяжести, действуют еще и сила трения в месте подвеса и сила сопротивления среды, то его колебания будут затухающими.

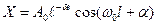(4)

где: 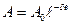-амплитуда – колебаний в произвольный момент времени t; 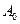- амплитуда в начальный момент времени; 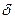- коэффициент затухания.

Логарифм двух последовательных амплитуд, отличающихся друг от друга на время, равное периоду колебаний, называется логарифмическим дискриментом затуханий.

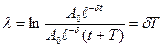(5)

Амплитуда затухающих колебаний:

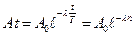(6)

n – число колебаний маятника за время t.

Момент инерции маятника:

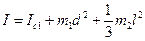(7)

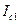- момент инерции груза относительно оси, проходящей через его центр массы параллельно оси О. m₁ – масса груза; m₂ – масса стержня;

Величину найдем с помощью выражения:

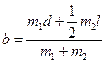(8)

Ход работы:

1. При помощи весов находим массу груза: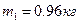

2. При помощи весов находим массу стержня: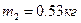

3. Устанавливаем груз на стержне на расстоянии .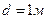

4. Приводим маятник в колебание. Пропускаем несколько колебаний включаем секундомер. Отсчитав 20-30 колебаний и соответствующий промежуток времени, определяем период колебаний: , ,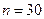

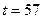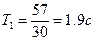
5. Устанавливаем груз на стержне на расстоянии 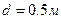и снова определяем период колебаний маятника: , ,

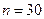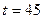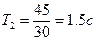
6. Сравниваем значения периодов колебаний, найденных экспериментально, со значениями, рассчитанными по формулам (3), (7) и (8). Делаем также заключение о влиянии положения груза на период колебаний маятника.

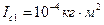
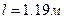
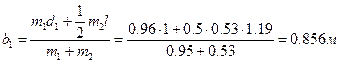
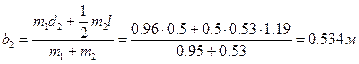
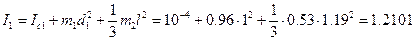
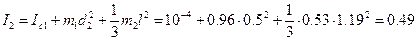
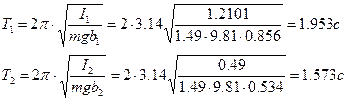
7. Меняем стальной груз на алюминиевый диск. Приводим маятник в колебание.

8. Измеряем секундомером время 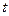, в течении которого произошло n колебани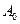й. и 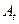- амплитуды в начале и в конце выбранного промежутка времени: , ,

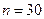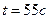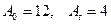
9. По формуле (6) определяем логарифмический дискремент затухания. Затем, найдя предварительно период колебаний, рассчитываем по формуле (5) коэффициент затухания.

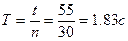
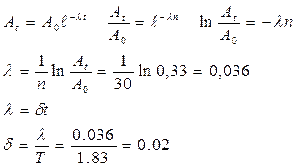
Вывод:чем ближе груз находится к концу стержня, тем период колебания становится больше. Научился определять период колебания, логарифмический дискремент затухания и коэффициент затухания.