Период малых колебаний физического маятника

Если амплитуда колебаний 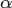мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

.

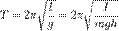22.Бие́ния — явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. Распространение такого вида колебаний менее эффективно. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.

Биения звука можно слышать при настройке струнного музыкального инструмента по камертону. Если частота струны незначительно отличается от частоты камертона, то слышно, что звук пульсирует — это и есть биения. Струну нужно подтягивать или ослаблять так, чтобы частота биений уменьшалась. При совпадении высоты звука с эталонным биения полностью исчезают. Биения звука также можно услышать при игре на музыкальных инструментах, например пианино или гитаре, когда различной высоты звуки создают интервалы и многозвучия (аккорды).

Эффект биений можно использовать для преобразования частоты сигналов.

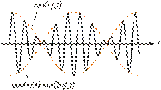Представление периодической функции связывают с понятиемгар­монического анализа сложного периодического колебания,илиразложения Фурье.*Слагаемые ряда Фурье, определяющие гармонические колебания с частотами w₀, 2w₀, 3w₀, ..., называютсяпервой (или основной),второй, третьейи т. д.гармониками сложного периодического колебания.

Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть 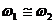, и пусть для определенности 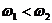. Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

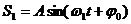
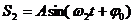
получим уравнение суммарного колебания:

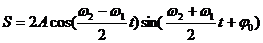
Полученное результирующее колебание не является гармоническим.

23.При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

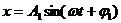
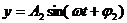
исключив время, получим:

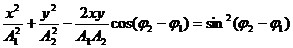
В общем случае это - уравнение эллипса. Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или 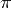вырождаются в отрезки прямых, а при разности фаз 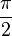и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.