Приложение. Теория малых колебаний физического маятника

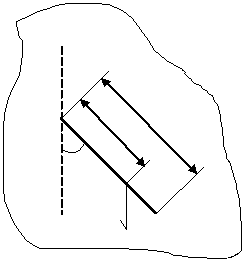
mg

φ

o

c

O’

Рисунок 3 3. Приведенная длина

Физическим маятником называется любое тело, которое под действием силы тяжести может свободно качаться вокруг неподвижной горизонтальной оси, называемой осью качаний. Точка пересечения оси качаний с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника (т. О на рис. 3). Очевидно, в положении равновесия центр масс маятника (т. С) находится на вертикальной прямой, проходящей через точку подвеса (φ = 0).

Движение маятника описывается основным уравнением динамики вращательного движения вокруг неподвижной оси:

,

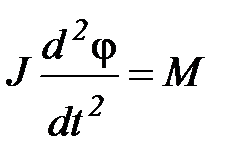где J – момент инерции маятника относительно оси вращения, φ – угол отклонения маятника от положения равновесия, М – суммарный момент внешних сил, действующих на маятник относительно оси вращения.

В экспериментальных установках обычно моменты силы трения в оси и силы сопротивления воздуха пренебрежимо малы. Поэтому М_с = – mgd sinφ, где

d = │ОС│ – расстояние от оси качания до центра масс, m – масса маятника,
g – ускорение свободного падения, а знак " – " указывает на то, что момент силы тяжести стремится возвратить маятник в положение равновесия. Таким образом, уравнение движения маятника имеет вид:

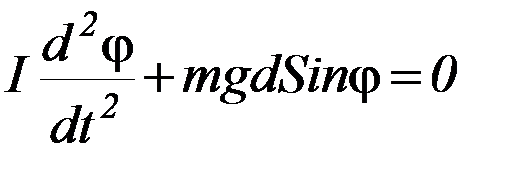(П-1)

В случае малых отклонений маятника от положения равновесия (т.е. φ << 1) можно положить sin φ ≈ φ. Тогда уравнение (П-1) примет вид:

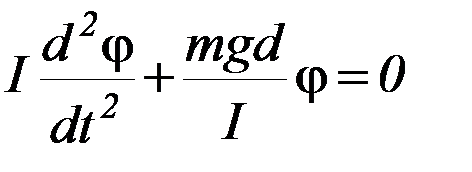(П-2)

Легко убедиться, что решением этого уравнения является функция

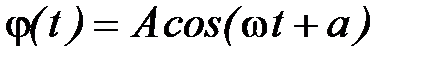
где 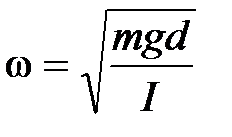, а А и α – произвольные постоянные, т.е. величина φ(t) совершает гармонические колебания с циклической частотой ω. Амплитуда А и начальная фаза колебаний α зависят от способа возбуждений колебаний, т.е. определяются значениями φ и 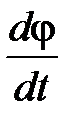в момент времени t = 0. Частота колебаний ω определяется только параметрами маятника m, J, d.

Таким образом, при малых углах отклонения от положения равновесия колебания физического маятника являются гармоническими с периодом

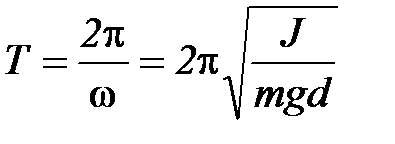, (П-3)

причем период колебаний не зависит ни от начальной фазы, ни от амплитуды колебаний, а определяется только параметрами маятника.

Согласно теореме Гюйгенса-Штейнера момент инерции маятника J относительно оси вращения можно представить в виде:

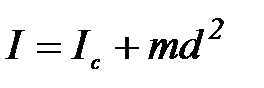, (П-4)

где J_c – момент инерции маятника относительно оси, проходящей через его центр масс.

Используя (П-4), формулу (П-3) можно переписать следующим образом:

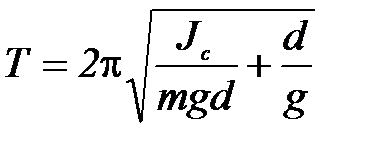(П-5)

Частным случаем физического маятника является математический маятник. Это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке – центре масс маятника С. Для математического маятника длиной 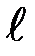имеем: d = 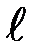. J_c = 0. Тогда формула (П-5) принимает вид:

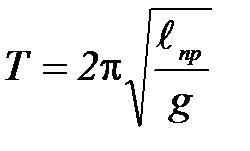(П-6)

Сравнение формул (П-5) и (П-6) показывает, что период колебаний физического маятника равняется периоду колебаний математического маятника длиной

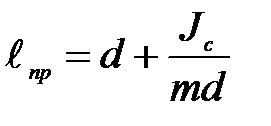(П-7)

Величину l_пр называют приведённой длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

Как следует из (П-7), приведенная длина физического маятника больше, чем расстояние от оси качания до центра масс маятника. Точка О, находящаяся от точки 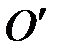на расстоянии l_пр вдоль прямой, соединяющей точку подвеса с центром масс, называется центром качаний. Если маятник подвесить в точке 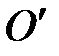, то период его колебаний будет тот же, что и при подвешивании в точке О. Действительно, при подвешивании маятника в точке 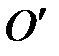, из (П-5) получаем следующее выражение для периода колебаний:

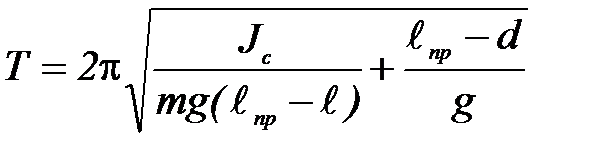(П-8)

Из (П-7) имеем: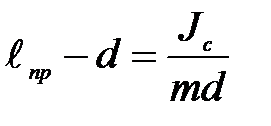

Тогда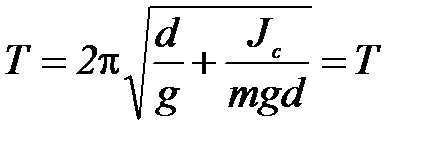

Таким образом, период колебаний физического маятника не изменяется при перемещении оси качаний в центр качаний.

Контрольные вопросы.

1. Какие предположения используются при построении теоретической модели колебаний маятника? Как их проверить?

2. Дайте определение понятию «физический маятник». Приведите примеры.

3. Дайте определение понятию «математический маятник»?

4. Сформулируйте определение длины физического маятника.

5. В чем состоит метод измерения ускорения свободного падения с помощью математического маятника?

6. Как повысить точность измерения ускорения свободного падения с помощью оборотного маятника?

7.В чем состоит метод оборотного маятника определения ускорения свободного падения?