Дифференциальное исчисление функций одной переменной 1 страница
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Методическое пособие
Хабаровск
Издательство ДВГУПС
УДК 517.2(075.8)
ББК В 161.54 я 73
В 656
Рецензент:
доцент кафедры «Высшая математика»,
кандидат физико-математических наук
Виноградова П.В.
Войтюк М.И.
| В 656 | Дифференциальное исчисление функций одной переменной. Методическое пособие. / М.И. Войтюк, В.Г. Гамалей, – Хабаровск : изд-во ДВГУПС, 2007. –75 с. |
Методическое пособие соответствует ГОС ВПО дисциплины “Высшая математика”, “Математический анализ” всех направлений и специальностей.
Изложены краткие теоретические сведения по дифференциальному исчислению функции одной переменной, рассмотрены примеры исследования и построения графиков функции с помощью производной, приведены варианты индивидуальных заданий.
Пособие предназначено для студентов инженерных и экономических специальностей первого курса дневной формы обучения, изучающих дисциплину “Высшая математика”, “Математический анализ” Рекомендуется преподавателям для проведения практических занятий и самостоятельной работы студентов.
УДК 517.2(075.8)
ББК В 161.54 я 73
© ГОУ ВПО «Дальневосточный государственный
университет путей сообщения» (ДВГУПС), 2007
Введение
Пособие содержит весь необходимый материал по дифференциальному исчислению функций одной переменной, изучаемый студентами инженерно-технических и экономических специальностей университетов. Для углубленного изучения этого раздела в конце пособия приведен список рекомендуемой учебной литературы.
Пособие состоит из восьми параграфов, в каждом из которых содержатся необходимые теоретические сведения и подробно разобранные примеры.
В последнем параграфе приведены варианты индивидуальных заданий для студентов всех специальностей дневной формы обучения.
1. Понятие производной, её геометрический смысл
1.1. Понятие производной
Пусть функция 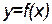 определена в точке x0 и некоторой ее окрестности, x–точка из этой окрестности. Разность x–x0 обозначим через Δx и назовем приращением аргумента, а разность f(x)–f(x0) обозначим через Δy и назовем приращением функции.
определена в точке x0 и некоторой ее окрестности, x–точка из этой окрестности. Разность x–x0 обозначим через Δx и назовем приращением аргумента, а разность f(x)–f(x0) обозначим через Δy и назовем приращением функции.
Итак, Δx = x–x0, Δy = f(x)–f(x0). Из равенства Δx = x–x0 получаем равенство x = x0 +Δx, тогда Δy = f(x0 + Δx)– f(x0).
Производной функции 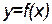 в точке x0 в обозначении
в точке x0 в обозначении 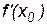 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.
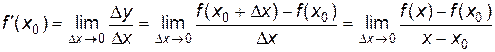 .
.
Производные элементарных функций представлены в табл. 1.
Таблица 1
1. 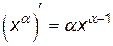 . 2. . 2. 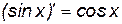 . 3. . 3. 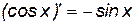 . 4. . 4. 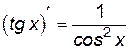 5. 5. 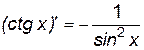 . . | 6. 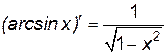 . 7. . 7. 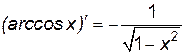 . 8. . 8. 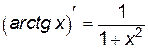 . 9. . 9. 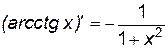 . . | 10. 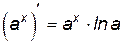 . 11. . 11. 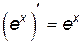 . 12. . 12. 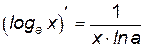 . 13. . 13. 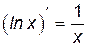 . . |
1.2. Геометрический смысл производной
Рассмотрим геометрический смысл производной.
На рис. 1 изображен график непрерывной функции 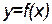 . Точка M0 на графике имеет координаты (x0,
. Точка M0 на графике имеет координаты (x0, 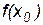 ). Прямая M0M является касательной для линии
). Прямая M0M является касательной для линии 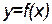 и наклонена к оси Ox под углом
и наклонена к оси Ox под углом 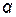 .
.
Геометрическое истолкование производной состоит в том, что угловой коэффициент касательной к графику функции 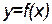 в точке с абсциссой x0 равен производной этой функции в точке x0:
в точке с абсциссой x0 равен производной этой функции в точке x0:
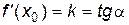 (1.1)
(1.1)
Очевидно, что уравнение касательной M0K имеет вид:
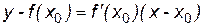 (1.2)
(1.2)

Рис. 1.
Пример 1.1. Составить уравнение касательной к параболе 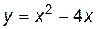 в точке, гдеx = 1.
в точке, гдеx = 1.
Решение.
Подставляя в уравнение параболы заданную абсциссу точки касания 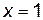 , найдем её ординату: y = -3.
, найдем её ординату: y = -3.
Для определения углового коэффициента касательной находим производную 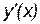 и вычисляем её значение в точке
и вычисляем её значение в точке 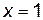 :
:
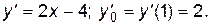
Подставляя значения 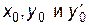 в уравнение (1.2), получим уравнение касательной
в уравнение (1.2), получим уравнение касательной
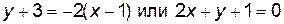 .
.
Пример 1.2. Составить уравнение касательной, проведенной к кривой 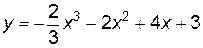 , параллельно прямой
, параллельно прямой 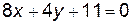 .
.
Решение.
По условию, касательная к заданной кривой параллельна прямой 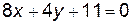 , следовательно угловые коэффициенты этих прямых должны быть равны.
, следовательно угловые коэффициенты этих прямых должны быть равны.
Угловой коэффициент касательной для кривой:
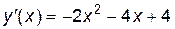 .
.
Найдем угловой коэффициент касательной прямой. для этого сведем уравнение к виду 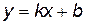 .
.
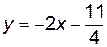 ,
, 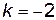 .
.
Приравняем угловые коэффициенты и решим полученное квадратное уравнение:
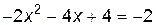 ,
, 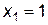 ,
, 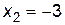 .
.
Найденные корни являются абсциссами точек, через которые проходит касательная к графику функции 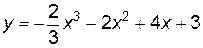 . Найдем ординаты этих точек:
. Найдем ординаты этих точек:
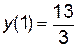 ,
, 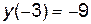 .
.
Составим уравнения касательных по формуле (1.2)
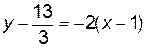 ,
, 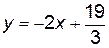
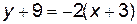 ,
, 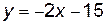 .
.
2. Правила дифференцирования.
Производная сложной функции
2.1. Правила дифференцирования
Правила дифференцирования позволяют находить производные суммы (разности), произведения и частного двух функций:
1. 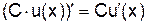 .
.
2. 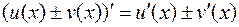 .
.
3. 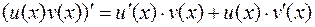 .
.
4. 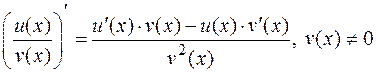 .
.
Замечание. Свойство 2 выполняется для алгебраической суммы любого количества функций.
Пример 2.1. Пользуясь формулами дифференцирования, найти производные следующих функций: а) 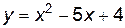 ; б)
; б) 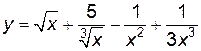
Решение.
а) Используя таблицу производных, первое и второе свойства получим:
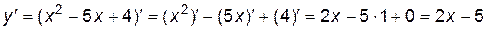 ;
;
б) Вводя дробные и отрицательные показатели, преобразуем данную функцию:
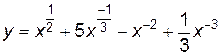 .
.
Тогда, используя производную степенной функции, свойства 1 и 2 будем иметь:
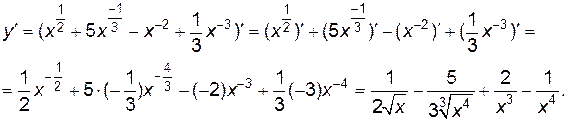
Пример 2.2. Найти производную функции 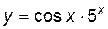 :
:
Решение.
Воспользовавшись свойством 3 получим:
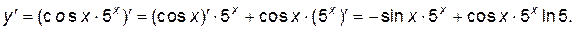
Пример 2.3. Найти производную функции 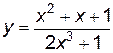 .
.
Решение.
Для решения примера используем свойство 4 производных.
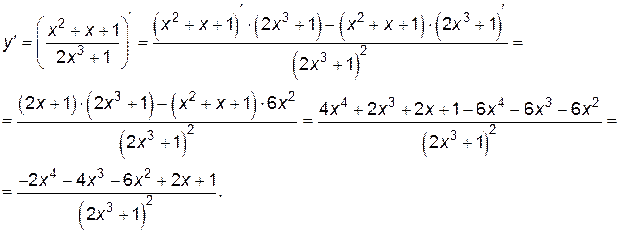
2.2. Производная сложной функции
Рассмотрим дифференцирование сложной функции.
Пусть 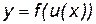 является сложной функцией, составленной из функции
является сложной функцией, составленной из функции 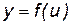 ,
, 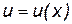 , где u – промежуточный аргумент. Покажем, как найти производную сложной функции, зная производную для функции
, где u – промежуточный аргумент. Покажем, как найти производную сложной функции, зная производную для функции 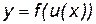 (её будем обозначать через
(её будем обозначать через 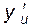 ) и производную
) и производную 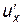 для функции
для функции 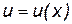 .
.
Теорема 1. Если функция 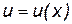 имеет производную
имеет производную 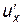 в точке x, а функция
в точке x, а функция 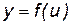 имеет производную
имеет производную 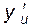 в точке
в точке 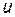 (
( 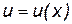 ), то сложная функция
), то сложная функция 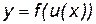 в точке x имеет производную
в точке x имеет производную 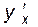 , причем
, причем
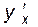 =
= 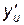
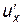 .
.
Иначе, производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.
Пример 2.4. Найти производную функции 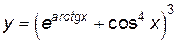 .
.
Решение.
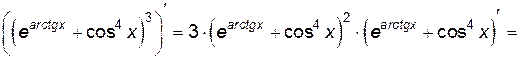
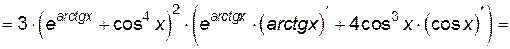
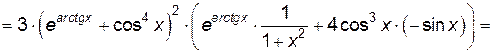
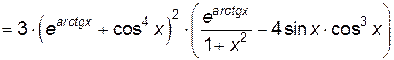 .
.
Пример 2.5.Найти производную функции
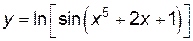 .
.
Решение.
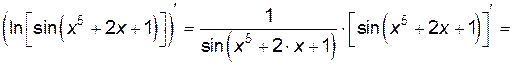
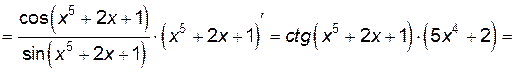
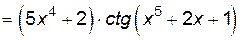 .
.
3. Дифференциал функции
Пусть функция в точке x0 имеет производную. По определению производной (п.1.1) 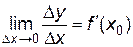 , поэтому по свойствам предела можно записать
, поэтому по свойствам предела можно записать 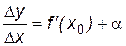 , где
, где 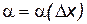 – бесконечно малая при
– бесконечно малая при 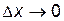 .Отсюда
.Отсюда
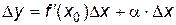 . (3.1)
. (3.1)
При 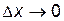 второе слагаемое в равенстве (3.1) является бесконечно малой высшего порядка, по сравнению с
второе слагаемое в равенстве (3.1) является бесконечно малой высшего порядка, по сравнению с 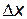 :
: 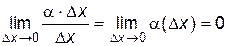 , поэтому
, поэтому 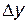 и
и 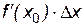 – эквивалентные бесконечно малые (при
– эквивалентные бесконечно малые (при 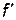 (x0)
(x0) 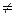 0).
0).
Таким образом, приращение функции 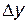 состоит из двух слагаемых, первое из которых
состоит из двух слагаемых, первое из которых 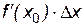 является главной частью приращения
является главной частью приращения 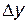 , линейной относительно
, линейной относительно 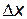 (при
(при 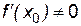 ).
).
Дифференциаломфункции 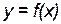 в точке
в точке 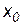 называется главная часть приращения функции и обозначается:
называется главная часть приращения функции и обозначается: 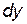 или
или 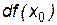 . Следовательно,
. Следовательно,
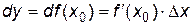 . (3.2)
. (3.2)
Пример 3.1. Найти дифференциал и приращение функции 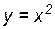 при: 1) произвольных
при: 1) произвольных 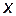 и
и 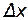 ; 2)
; 2) 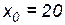 ,
, 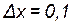 .
.
Решение.
1) 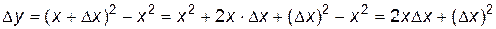 ,
, 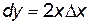 .
.
2) Если 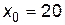 ,
, 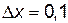 , то
, то 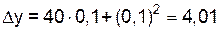 ;
; 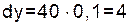
Запишем равенство (3.1) в виде:
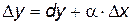 (3.3)
(3.3)
Приращение 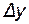 отличается от дифференциала
отличается от дифференциала 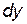 на бесконечно малую высшего порядка, по сравнению с
на бесконечно малую высшего порядка, по сравнению с 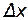 , поэтому в приближенных вычислениях пользуются приближенным равенством
, поэтому в приближенных вычислениях пользуются приближенным равенством 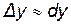 , если
, если 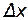 достаточно мало.
достаточно мало.
Учитывая, что 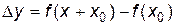 , получаем приближенную формулу:
, получаем приближенную формулу:
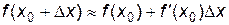 (3.4)
(3.4)
Пример 3.2. Вычислить приближенно 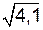 .
.
Решение. Рассмотрим: функцию 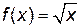 , при
, при 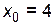 ,
, 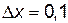 . Тогда
. Тогда 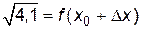 .
.
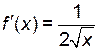 ,
, 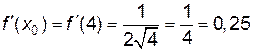
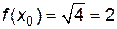 .
.
Используя формулу (3.4), получим:
Значит 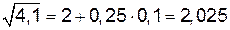
4. Дифференцирование обратной функции, функций
заданных неявно, параметрически.
Логарифмическое дифференцирование
4.1. Дифференцирование обратной функции
Введем правило для нахождения производной обратной функции.
Теорема. Пусть функция 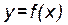 определена на промежутке Х, непрерывна, монотонна (возрастает или убывает) и дифференцируема на Х. Если ее производная
определена на промежутке Х, непрерывна, монотонна (возрастает или убывает) и дифференцируема на Х. Если ее производная 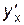 в точке
в точке 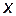 не равна нулю, то обратная функция
не равна нулю, то обратная функция 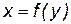 имеет производную
имеет производную 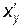 в точке
в точке 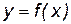 , причем
, причем
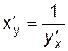 (4.1)
(4.1)
Доказательство. Функция 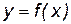 определена, непрерывна и монотонна на промежутке Х, тогда она имеет обратную функцию
определена, непрерывна и монотонна на промежутке Х, тогда она имеет обратную функцию 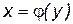 , определенную, непрерывную и монотонную на промежутке Y.
, определенную, непрерывную и монотонную на промежутке Y.
Если значение аргумента 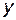 получает приращение
получает приращение 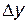 , отличное от нуля, то в силу монотонности функции
, отличное от нуля, то в силу монотонности функции 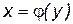 функция
функция 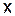 получает приращение
получает приращение 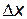 и
и 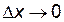 . В силу непрерывности функции
. В силу непрерывности функции 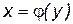 :
: 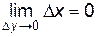 .
.
Следовательно, 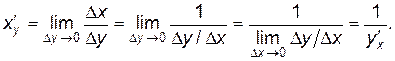
Итак, 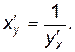
Теорема доказана.
Пример 4.1. Если 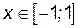 ,
, 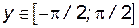 , то функции
, то функции 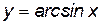 ,
, 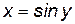 являются взаимно обратными, причем
являются взаимно обратными, причем 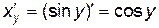 . Если
. Если 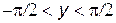 (при этом
(при этом 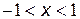 ), то
), то 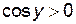 , поэтому
, поэтому 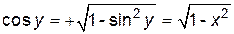 .
.
По формуле (4.1) имеем: 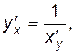 тогда
тогда
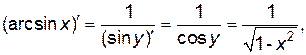 (
( 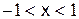 ).
).
4.2. Дифференцирование функций, заданных неявно
Не всегда функция бывает представлена в виде 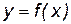 . Например, уравнение
. Например, уравнение 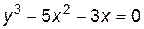 задает функцию y, которую можно из этого уравнения выразить через
задает функцию y, которую можно из этого уравнения выразить через 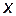 :
: 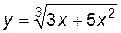 .
.
Пусть переменные 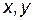 связаны между собой некоторым уравнением
связаны между собой некоторым уравнением
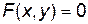 (4.2)
(4.2)
причем y является функцией от x. Тогда говорят, что функция y задана неявно уравнением (4.2).
Не всегда функции, заданные неявно могут быть выражены явно через элементарные функции. Так, из уравнения 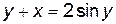 , которое неявно задает функцию y, нельзя выразить y явно через элементарные функции.
, которое неявно задает функцию y, нельзя выразить y явно через элементарные функции.
Для того чтобы найти производную y' для функции, заданной неявно уравнением (4.2) надо найти производные по x от обеих частей этого уравнения, помня, что y – функция от x и приравнять эти производные. Из полученного уравнения найти y'.
Пример 4.2. Найти производную функции, заданной неявно уравнением 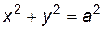 .
.
Решение.
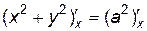 .
.
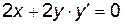 .
.
Отсюда 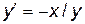 .
.
4.3. Дифференцирование функций, заданных параметрически
Рассмотрим задание линии на плоскости, при котором переменные
x, y являются функциями третьей переменной t (называемой параметром):
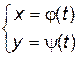 (4.3)
(4.3)
Каждому значению t из некоторого интервала соответствуют определенные значения x и y, а, следовательно, определенная точка M 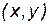 плоскости. Когда t пробегает все значения из заданного интервала, то точка M
плоскости. Когда t пробегает все значения из заданного интервала, то точка M 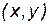 описывает некоторую линию L. Уравнения (4.3) называются параметрическими уравнениями линии L.
описывает некоторую линию L. Уравнения (4.3) называются параметрическими уравнениями линии L.
Если функция 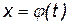 на некотором интервале изменения t имеет обратную функцию
на некотором интервале изменения t имеет обратную функцию 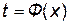 , то подставляя это выражение в уравнение
, то подставляя это выражение в уравнение 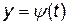 , получим
, получим 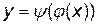 , которое задает y как функцию от x.
, которое задает y как функцию от x.
Пусть 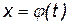 ,
, 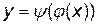 имеют производные, причем
имеют производные, причем 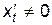 . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции 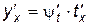 . На основании правила дифференцирования обратной функции
. На основании правила дифференцирования обратной функции 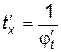 , имеем:
, имеем:
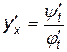 (4.4)
(4.4)
Полученная формула (4.4) позволяет находить производные для функций, заданных параметрически.
Пример 4.3. Пусть функция y, зависящая от x, задана параметрически:
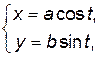
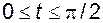 .
.
