Понятие функции на множестве
Введем понятие функции через бинарное отношение.
Определение 1.
Функцией называется любое бинарное отношение, которое не содержит двух пар с одинаковыми первыми элементами и разными вторыми.
Если f – функция, то множество Df мы будем называть областью определения функции f, а множество Rf – областью значения функции.
ПРИМЕР 1.
1. {(1,1); (2,3); (3,2)}, есть функция с областью определения {1,2,3} и это же множество является ее областью значений;
2. Бинарное отношение {(1, 2); (2, 2); (пешка, ферзь); (ладья, слон)} – есть функция с областью определения {1, 2, пешка, ладья} и областью значения {2, ферзь, слон};
3. Бинарное отношение {(1,2); (1,1); (2,3)} не является функцией, поскольку содержит пары с одинаковыми первыми и разными вторыми элементами;
4. {((x, y), x+y) : (x,y)  } - функция с областью определения в
} - функция с областью определения в 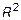 и областью значений в
и областью значений в 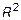 .
.
| |
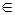 f, то элемент y называют значением функции f на x, или образом элемента x при f, поэтому элемент y мы будем обозначать f(x): y = f(x). Поскольку f – функция, то имеется только одна пара (x, y) с первой компонентой x и второй y, принадлежащая f. Достаточно часто говорят, что y является образом элемента x, а элемент x является прообразом элемента y. К функциям, поскольку они являются множествами, применимо понятие «равенство».
f, то элемент y называют значением функции f на x, или образом элемента x при f, поэтому элемент y мы будем обозначать f(x): y = f(x). Поскольку f – функция, то имеется только одна пара (x, y) с первой компонентой x и второй y, принадлежащая f. Достаточно часто говорят, что y является образом элемента x, а элемент x является прообразом элемента y. К функциям, поскольку они являются множествами, применимо понятие «равенство». Определение 2.
Функции f и g равны между собой тогда и только тогда, когда они состоят из одних и тех же элементов:
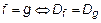 и
и 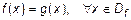 .
.
Итак, пусть задана область определения функции f – множество Df. Часто возникает задача – найти область значений этой функции - множество Rf. Точно это сделать бывает трудно, поэтому иногда проще указать множество Y, такое, что Rf 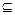 Y. Удобно ввести следующие определения.
Y. Удобно ввести следующие определения.
Определение 3.
Если Df 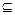 X и Rf
X и Rf 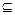 Y, то говорят, что функция f определена в множестве X и принимает свои значения в множестве Y.
Y, то говорят, что функция f определена в множестве X и принимает свои значения в множестве Y.
Определение 4.
Если Df = X и Rf 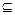 Y, то говорят, что функция f определена на множестве X и принимает свои значения в множестве Y.
Y, то говорят, что функция f определена на множестве X и принимает свои значения в множестве Y.
Определение 5.
Если, кроме того, что Df = X, выполнено еще условие Rf = Y, то отображение (функцию) f называют отображением множества X "на" Y, или сюръекцией. Заметим, что каждая функция f является сюръекцией множества Df на Rf.
Определение 6.
Функция f называется инъективной, или инъекцией, если из того, что f(a) = f(b), следует, что a = b.
Определение 7.
Инъективное отображение множества X на множество Y называется однозначным (биективным), или просто биекцией типа X 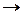 Y.
Y.
| |
1. Для заданной квадратичной функции f = {(x,y)  : y = x2 } проверить, является ли она биекцией. Функция f является отображением множества R на множество
: y = x2 } проверить, является ли она биекцией. Функция f является отображением множества R на множество 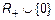 . Для проверки биективности функции f необходимо проверить, является ли она еще и инъекцией. Квадратичная функция f такова, что f(1) = f(-1), однако отсюда не следует, что 1 = -1. Таким образом, показали, что отображение f не является инъекцией. Следовательно, биективным такое отображение f также не является.
. Для проверки биективности функции f необходимо проверить, является ли она еще и инъекцией. Квадратичная функция f такова, что f(1) = f(-1), однако отсюда не следует, что 1 = -1. Таким образом, показали, что отображение f не является инъекцией. Следовательно, биективным такое отображение f также не является.
2. Рассмотрим функцию g, которая каждому элементу x 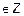 ставит в соответствие число g(x) = 2x+1. Покажем, что заданная таким образом функция g является взаимно-однозначным соответствием между Z и множеством нечетных целых чисел. Действительно, из того, что 2x1+1 = 2x2+1, следует, что x1 = x2.
ставит в соответствие число g(x) = 2x+1. Покажем, что заданная таким образом функция g является взаимно-однозначным соответствием между Z и множеством нечетных целых чисел. Действительно, из того, что 2x1+1 = 2x2+1, следует, что x1 = x2.
В последнем примере было установлено взаимно-однозначное соответствие между множеством Z и его собственным подмножеством. Вообще говоря, справедливо следующее утверждение.
Теорема 1.
Множество M бесконечно тогда и только тогда, когда существует взаимно-однозначное соответствие между самим множеством M и его собственным подмножеством.
Важно!!!
Из определения суперпозиции бинарных отношений f и g следует, что когда f и g являются функциями, то значение их суперпозиции fg на элементе x вычисляется следующим образом: 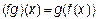 – и означает, что если f:
– и означает, что если f: 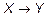 , а g:
, а g: 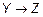 , тогда fg :
, тогда fg : 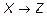 .
.
Определение 8.
Когда для заданной функции f отношение f -1 является также функцией, то это отношение называется функцией обратной к f и обозначается f -1.
Теорема 2.
Для любой заданной функции f обратная ей функция f -1 существует тогда и только тогда, когда f – инъективна.
Доказательство.
Необходимость. Предположим, что для заданной функции f обратная к ней функция f -1 существует. Покажем, что в этом случае f – инъективна.
Доказательство будем проводить от противного. Пусть f не является инъективным отображением. Это означает, что существует, по крайней мере, две пары (a, c) 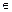 f, (b, c)
f, (b, c) 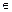 f, a
f, a 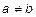 . Следовательно, f -1 содержит пары (c, a), (c, b) и поскольку
. Следовательно, f -1 содержит пары (c, a), (c, b) и поскольку 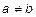 , бинарное отношение f -1 не является функцией. Таким образом мы получили противоречие. Значит, исходное предположение о том, что f не является инъективным отображением, ложно. На этом и завершается доказательство необходимости приведенного утверждения. Доказательство достаточности будет приведено немного позднее.
, бинарное отношение f -1 не является функцией. Таким образом мы получили противоречие. Значит, исходное предположение о том, что f не является инъективным отображением, ложно. На этом и завершается доказательство необходимости приведенного утверждения. Доказательство достаточности будет приведено немного позднее.
| |
В первой лекции говорилось о мощности конечных множеств, при этом мощностью конечного множества называлось число его элементов. Теперь перейдем теперь к множествам с бесконечным числом элементов. Как сравнивать такие множества априори непонятно - и в том и в другом множестве имеется бесконечно много элементов. Какая из двух бесконечностей больше? Поэтому, когда сравнивают бесконечные множества, обычно прибегают к такому трюку: пытаются построить отображение одного множества на другое, и если это удается, да еще отображение оказывается взаимно-однозначным, то множества объявляют "равными".
Определение 9.
Говорят, что множество A эквивалентно множеству B, если существует биективное отображение f: 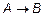 (см.: Л.3, опр.4).
(см.: Л.3, опр.4).
Под словами "биективное отображение" понимают взаимно-однозначное отображение "на". Эту биекцию записывают как A~B.
ПРИМЕР 3.
1. Множество N и множество четных натуральных чисел эквивалентны. Необходимая биекция задается формулой f(n)=2n, 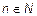 .
.
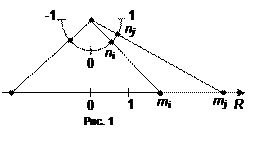 2. Множества (0,1) и R эквивалентны. Этот пример немного неожиданен, поскольку утверждается, что число точек открытого интервала (0,1) равно числу точек всей вещественной прямой. Нужная нам биекция строится следующим образом (рис. 1). Представим интервал (-1,1) в виде некоторой полуокружности. Множество действительных чисел представим некоторой прямой. Из центра полуокружности проведем любую прямую линию в некоторую точку (mi) на прямой R. Очевидно, что прямые линии, соединяют единственную точку
2. Множества (0,1) и R эквивалентны. Этот пример немного неожиданен, поскольку утверждается, что число точек открытого интервала (0,1) равно числу точек всей вещественной прямой. Нужная нам биекция строится следующим образом (рис. 1). Представим интервал (-1,1) в виде некоторой полуокружности. Множество действительных чисел представим некоторой прямой. Из центра полуокружности проведем любую прямую линию в некоторую точку (mi) на прямой R. Очевидно, что прямые линии, соединяют единственную точку 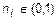 на полуокружности с единственной точкой
на полуокружности с единственной точкой 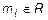 вещественной прямой и задают биекцию между точками интервала (0,1) и точками всей прямой, являющейся множеством R.
вещественной прямой и задают биекцию между точками интервала (0,1) и точками всей прямой, являющейся множеством R.
Определение 10.
| |
Теорема 3.
Два конечных множества имеют одинаковую мощность тогда и только тогда, когда они эквивалентны.
Доказательство.
Необходимость. Пусть два конечных множества имеют одинаковую мощность |A|=|B|= n, т.е. A = {a1, a2,..., an}, B = {b1, b2,..., bn}. Отображение f: A 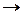 B, определенное по формуле f(ak) = bk, k = 1, ..., n, является биекцией и, следовательно, A~B.
B, определенное по формуле f(ak) = bk, k = 1, ..., n, является биекцией и, следовательно, A~B.
Достаточность. Пусть A~B и f: A 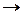 B – биекция, устанавливающая эту эквивалентность. Если A = {a1, a2,..., an }, то B = { f(a1), f(a2),..., f(an)}и элементы f(ak) попарно различны. Следовательно, |A|=|B|= n. Доказательство завершено.
B – биекция, устанавливающая эту эквивалентность. Если A = {a1, a2,..., an }, то B = { f(a1), f(a2),..., f(an)}и элементы f(ak) попарно различны. Следовательно, |A|=|B|= n. Доказательство завершено.
Определение 11.
Множество A называется счетным, если оно эквивалентно множеству натуральных чисел: A~N. В этом случае говорят, что множество A имеет счетную мощность.
Теорема 4.
Множество A имеет счетную мощность тогда и только тогда, когда элементы этого множества можно перенумеровать, используя все натуральные числа.
Доказательство.
Необходимость. Пусть множество A счетно. Это означает, что A~N. По определению эквивалентности существует биекция f: 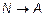 . Положим, что an= f(n),
. Положим, что an= f(n), 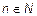 . Тогда A={a1, a2,... }, и тем самым мы перенумеровали элементы множества A.
. Тогда A={a1, a2,... }, и тем самым мы перенумеровали элементы множества A.
Достаточность. Пусть элементы множества A перенумерованы, т.е. A={a1,a2,...}. Определим отображение f: 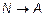 или f(n)=an,
или f(n)=an, 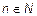 . Очевидно, что f – биекция и поэтому N~A. Доказательство завершено.
. Очевидно, что f – биекция и поэтому N~A. Доказательство завершено.
Теорема 5.
Объединение конечного или счетного набора конечных или счетных множеств конечно или счетно.
Теорема 6.
Множество Q рациональных чисел счетно.
Доказательство этого утверждения сводится к правилу пересчета всех рациональных чисел.
Итак, мы познакомились с конечными и бесконечными множествами. Было показано, что надо понимать под мощностью множеств в каждом из рассмотренных случаев. Однако возникает вполне естественный вопрос – а существуют множества с мощностью большей, чем счетная?
Мощность континуума
Теорема 7.
Множество M = (0,1) несчетно.
| |
Предположим, что множество M - счетно и, следовательно, элементы этого множества можно перенумеровать, используя все натуральные числа, т.е. M = {x1,x2,... }. Запишем числа 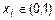 в виде десятичных дробей (без 9 в периоде):
в виде десятичных дробей (без 9 в периоде):
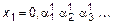
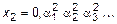
...
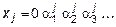
здесь 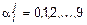 ; верхний индекс обозначает номер числа, а нижний – порядковый номер знака. Теперь образуем новое число
; верхний индекс обозначает номер числа, а нижний – порядковый номер знака. Теперь образуем новое число 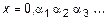 по следующему правилу:
по следующему правилу: 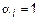 , если
, если 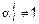 , и 0, если
, и 0, если 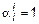 . Тогда очевидно, что
. Тогда очевидно, что 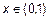 , но образованное таким образом новое число не совпадает ни с одним из пересчитанных чисел xi. Следовательно, интервал (0,1) содержит, как минимум, на 1 точку больше, чем есть натуральных чисел, и его мощность не равна мощности множества натуральных чисел. Мы доказали, что множество точек интервала (0,1) не счетно.
, но образованное таким образом новое число не совпадает ни с одним из пересчитанных чисел xi. Следовательно, интервал (0,1) содержит, как минимум, на 1 точку больше, чем есть натуральных чисел, и его мощность не равна мощности множества натуральных чисел. Мы доказали, что множество точек интервала (0,1) не счетно.
| |
Множество A имеет мощность континуума, если оно эквивалентно множеству точек интервала (0,1). Мощность континуума обозначают буквой c.
ПРИМЕР 4.
Пусть a<b – два действительных числа. Покажем, что интервал (a,b) имеет мощность континуума. В качестве биекции, устанавливающей эквивалентность множеств (a,b) и (0,1), можно рассматривать функцию f(x) = (b-a)x+a: (0,1) 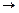 (a,b).
(a,b).
Теорема 8.
Существуют иррациональные числа. Более того, множество иррациональных чисел имеет мощность континуума.
Доказательство.
Поскольку 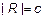 и
и 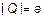 , а
, а 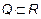 , мы получаем, что
, мы получаем, что 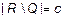 .
.
Заключение
В лекции заканчивается тема «Дискретная математика», однако на протяжении всего курса к ней необходимо будет возвращаться с целью расширения объема понятий и знаний. С целью лучшего восприятия остальных тем высшей математики объединим некоторые разделы дискретной математики с остальными темами. При этом нам придется столкнуться с такими разделами дискретной математики, как «Теория графов», «Логика», «Векторные пространства» и др. Важно целостное понимание всех разделов высшей математики на основе пройденного материала. Отметим следующее:
- функция – это множество пар, у которых одному первому элементу соответствует единственный второй элемент;
- как и у отношений, у функций есть обратная функция;
- суперпозиция функции есть «сложная функция» в классическом понимании;
- бесконечные множества имеют мощность;
- мощность 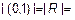
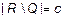 .
.
Литература
1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. – 384 с.
2. Москинова Г.И. Дискретная математика. – М.: Логос, 2002. – 240 с.
3. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2001.
4. Самсонов Б.Б. и др. Компьютерная математика. – Ростов-на-Дону: Феникс, 2002. – 512 с.
| |
