Примеры

1. Вычислить производную функции 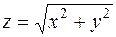в точке 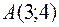по направлению:

а) биссектрисы первой координатной четверти.

б) радиуса-вектора точки А.

в) вектора .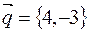

1) Находим частные производные функции и вычисляем их значения в точке А:

,

,

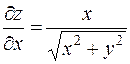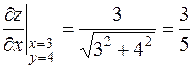
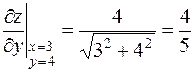
Подставляя в формулу (1), найдем производные функции 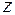в точке А по любому направлению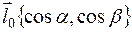

.

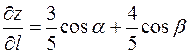2) найдем значения производной по указанным направлениям:

а) Для биссектрисы первого координатного угла 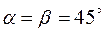, откуда искомая производная равна

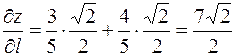
б) запишем координаты радиуса-вектора точки А: 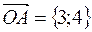, и найдем направляющие косинусы: , .

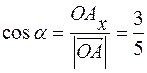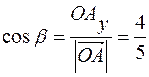Тогда для этого случая .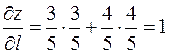

в) направляющие косинусы вектора : , .,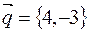

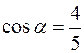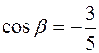откуда .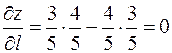

2. Вычислить производную функции 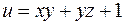по направлению вектора 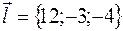в любой точке и в точках 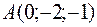и .

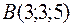1) Находим частные производные функции :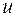

, ,

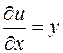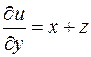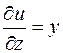
и направляющие косинусы вектора 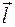, модуль которого :

, , .

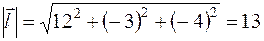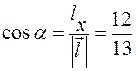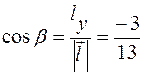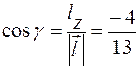2) Подставляя в (1), найдем производную функции 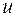по указанному направлению 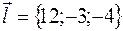в любой точке:

.

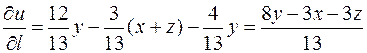3) Подставляя координаты точек А и В, получим производные функции

, .

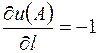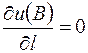3. Найти производную функции 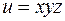в точке 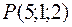в направлении, идущем от этой точки к точке .

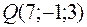1) Находим частные производные функции и вычисляем их значения в точке Р:

, ,

, ,

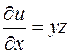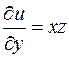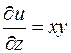
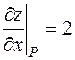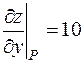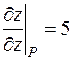
2) найдем координаты вектора: 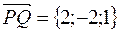, его модуль 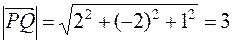и вычислим его направляющие косинусы: , , .

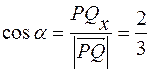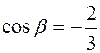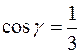Отсюда .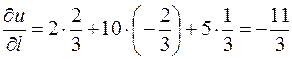

Знак минус указывает, что в данном направлении функция 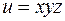убывает.

4. Найти точки, в которых функция 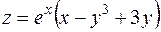стационарна (т.е. точки, в которых производная по любому направлению равна нулю).

Для того чтобы в некоторой точке функция была стационарна, необходимо и достаточно, согласно формуле (1), чтобы в этой точке все ее частные производные первого порядка одновременно обращались в нуль.

Найдем частные производные первого порядка:

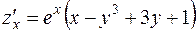и .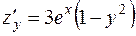

Решив систему уравнени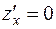й: и 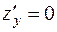, получим 2 точки, в которых функция стационарна: 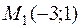.и .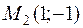

3. Градиент функции

Снова рассмотрим формулу производной по направлению:

.

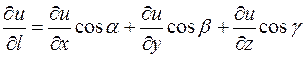Вторые множители в каждом из этих слагаемых являются, как мы уже отмечали, проекциями единичного вектора , направленного по вектору : .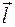

Возьмем теперь вектор, проекциями которого на координатные оси будут служить значения частных производных в выбранной точке 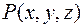. Назовем его градиентом функции и будем обозначать символами:

или .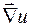

1°. Пусть — однозначная непрерывная функция, имеющая непрерывные частные производныеГрадиентом скалярной функции называется вектор, проекции которого на координатные оси Ох, Оу и Oz соответственно равны значениям частных производных этой функции 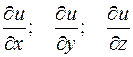, т. е.

.

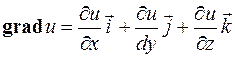На основании этого определения проекции вектора на координатные оси запишутся так:

; ; .

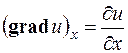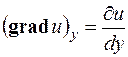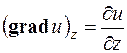Модуль вектора вычисляется по формуле:

.

Подчеркнем, что проекции градиента зависят от выбора точки 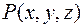и изменяются с изменением координат этой точки.Таким образом, каждой точке скалярного поля, задаваемого функцией поля , соответствует определенный вектор – градиент этой функции.

Связь градиента с производной по направлению

Из определения градиента следует, что производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления:

.

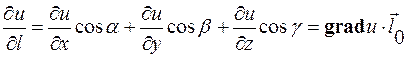Из определения скалярного произведения:

,

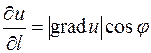где j - угол между и 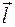. Отсюда видно, что производная по направлению достигает наибольшего значения, когда 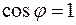, т.е. при j=0. Причем это наибольшее значение .

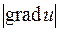Итак, направление градиента есть направление наискорейшего возрастания функции.