Применение производной в доказательстве тождеств
Доказательства тождества можно достигнуть иногда, если воспользоваться одним очевидным замечанием:
Если на некотором интервале функция тождественно равна постоянной, то ее производная на этом интервале постоянно равна нулю:
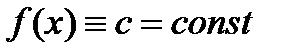 на
на 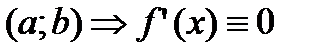 на
на 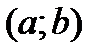 .
.
Задача 1. Проверить тождество:
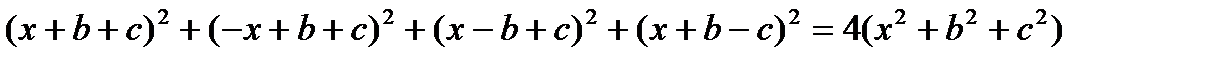 (1)
(1)
Доказательство: Рассмотрим функцию
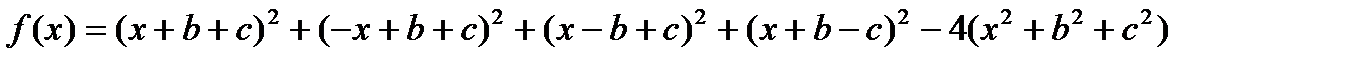
Вычислим ее производную (по х):
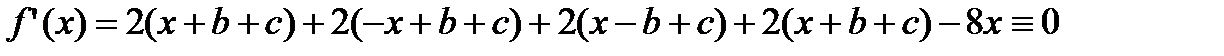
Поэтому (замечание) 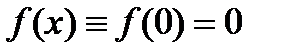 . Следовательно,
. Следовательно, 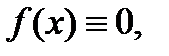 что равносильно тождеству (1).
что равносильно тождеству (1).
Задача 2. Проверить тождество:
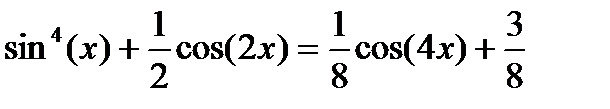 (2)
(2)
Доказательство: Рассмотрим функцию
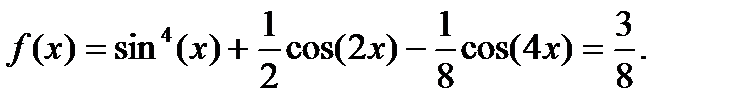
Докажем, что 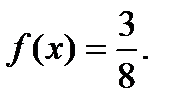
Найдем ее производную:
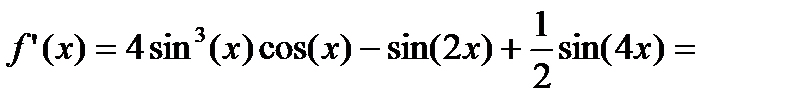
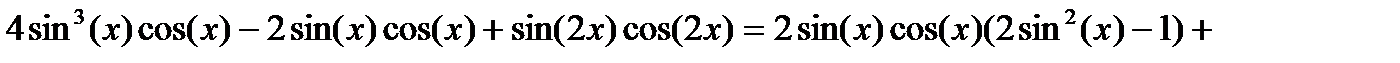
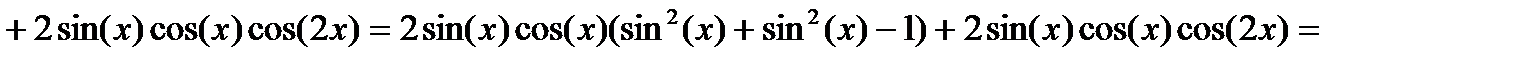
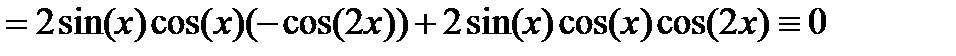
Значит 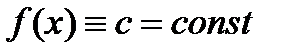
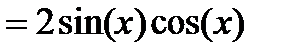
. При х=0 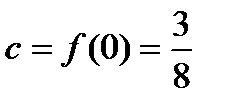 ,следовательно,тождество (2) верно.
,следовательно,тождество (2) верно.
В связи с рассмотренными примерами можно отметить, что при нахождении постоянной, интегрирования С полезно фиксировать значения переменной, по которой производится дифференцирование, таким образом, чтобы получить возможно более простые выкладки.
