Методом кусочно-линейной аппроксимации

Функция F(X) называется сепарабельной, если ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной, т.е. если

F(X) = F₁(x₁) + F₂ (x₂) + … + F_n (x_n) или 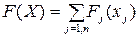(8.9)

(не исключено, что F_j(x_j) = 0 при некоторых j).

Пусть в задаче ВП (8.7), (8.8) и функция цели Z, и все ограничения φ_i являются сепарабельными. Тогда задача имеет вид: найти минимум (максимум) функции 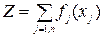при ограничениях

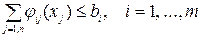(8.10)

Идея метода кусочно-линейной аппроксимации состоит в том, что все f_i и все φ_ij заменяются ломаными линиями, состоящими из прямолинейных отрезков. При этом исходная задача ВП заменяется новой, приближенной задачей, которая является задачей линейного программирования.

Эта задача решается обычным симплексным методом, и ее решение является приближенным решением исходной задачи ВП.

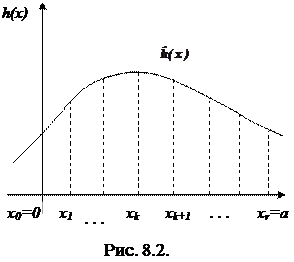
Рассмотрим кусочно-линейную аппроксимацию функции h(x) одной переменной, заданной на отрезке [0, a]. Разобьем этот отрезок на r частей точками x₀ < x₁ < … < x_r так, чтобы x₀=0, x_r=a (рис. 8.2). Вычислим значения функции h_k(x) (k=0, …, r) в этих точках. Соединим попарно точки (x_k, h_k) и (x_k+1, h_k+1) отрезками прямых. Состоящая из этих отрезков ломаная 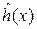аппроксимирует функцию h(x) на отрезке [0, a].

Уравнение участка ломаной 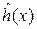между точками (x_k, h_k) и (x_k+1, h_k+1) имеет вид 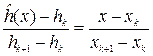(уравнение прямой по двум точкам). Если каждое из отношений в этом равенстве обозначить через λ, то получим:

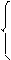x= λx_k+1 + (1- λ)x_k,

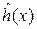= λh_k+1 + (1-λ)h_k причем 0 ≤ λ ≤ 1 (8.11)

Отметим, что для каждого x 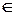[x_k, x_k+1] существует единственное значение λ, удовлетворяющее условия (8.11). Обозначив 1- λ = λ_k, λ= λ_k+1, можно переписать (8.10) в виде:

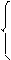x= λ_k x_k + λ _k+1 x_k+1,

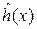= λ_k h_k + λ _k+1 h_k+1 (8.12)

где λ_k + λ _k+1=1, λ_k ≥0, λ _k+1≥0.

Таким образом, для любого x 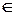[0, a] уравнение ломаной можно записать в виде: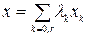

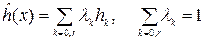и λ_k ≥ 0, (k=0, …,r) (8.13)

причем всегда отличны от нуля только два значения λ_k (если х является внутренней точкой k-го отрезка разбиения) или одно (если х совпадает с концом отрезка).

Возвращаясь к задаче ВП с сепарабельными функциями, отметим, что, прежде всего (в зависимости от системы ограничений) нужно определить интервал изменения каждой переменной x_j. Затем каждый этот интервал разбивается на части точками x_jk и с использованием формул (8.13) строится кусочно-линейная аппроксимация для функций f_i и φ_ij. После этого можно для исходной задачи (8.10) записать приближенную задачу:

найти максимум функции

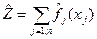
при ограничениях 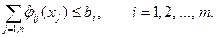(8.14)

x_j ≥ 0, j=1, 2, …, n

Поскольку приближенная задача (8.14) является задачей линейного программирования и мы обычно решаем ее симплексным методом (условия неотрицательности переменных записываем отдельно от остальных ограничений).

Пример 8.5. . . . . . .

В общем случае получаемое решение является лишь некоторым приближением оптимального решения исходной задачи. Улучшить точность приближения можно, разбивая на более мелкие части уже не исходные диапазоны изменения переменных, а другие, меньшие, взятые в окрестности полученного первого приближения. Недостатком метода является большое увеличение размерности задачи (т.е. числа переменных) при переходе к приближенной линейной модели.