Метод линейной аппроксимации.
Рассмотрим алгоритм метода линейной аппроксимации для решения задачи минимизации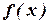 
при условии
;
.
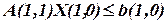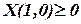Для данной допустимой точки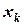 
найдем решение задачи линейного программирования 
:
;
,
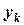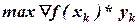
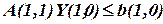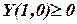где 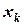- фиксированная допустимая точка, а 
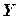- переменная, 
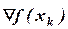-градиент функции. Далее с помощью направления 
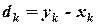получаем следующую точку 
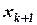. При этом при 
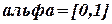любая точка 
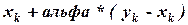,будет допустимой. Следует обратить внимание на то, что точка 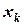дает зигзагообразное движение к точке оптимума, что замедляет сходимость.
Рассмотрим решение на примере задачи Нелинейная оптимизация с ограничениями.
Вариант работы №1.
Минимизировать функцию:
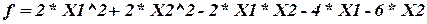
при наличии ограничений: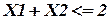 
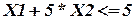
Примем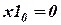 
; 
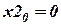. Тогда линейная аппроксимация имеет вид.
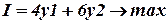
при наличии ограничений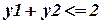 
;
.
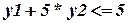Решение находим с помощью программы simpl_k.exe. Решение представлено таблицами
| -x1 | -x2 | B | |
| x3 | 1.00 | 1.00 | 2.00 |
| x4 | 1.00 | 5.00 | 5.00 |
| fmax | -4.00 | -6.00 | 0.00 |
ИСХОДНАЯ СИМПЛЕКС-ТАБЛИЦА СОСТАВЛЕНА.
| -x3 | -x4 | B | |
| x1 | 1.25 | -0.25 | 1.25 |
| x2 | -0.25 | 0.25 | 0.75 |
| fmax | 3.50 | 0.50 | 9.50 |
Задача решена
Графическое решение находим с помощью программы Lp_grafn.exe. Решение представлено рис. 1.
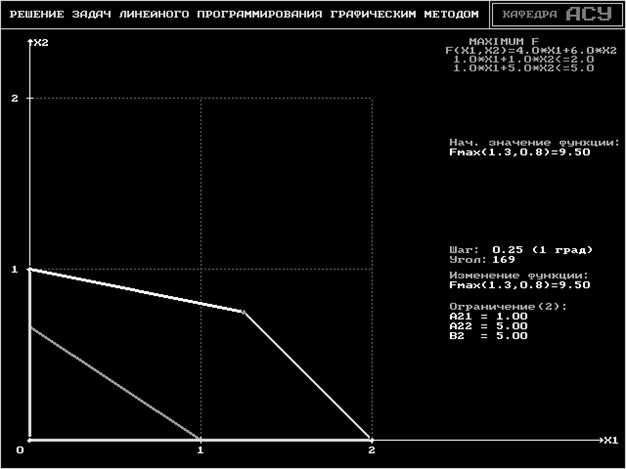
Рис. 1.
Далее с помощью направления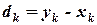 
получаем следующую точку 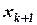. Решение получено с помощью пакета Microsoft Excel.
| Метод | линейной | аппрксим | нелинейн | задачи | оптимизации |
| x1 | x2 | Fmin | alfa | x1+x2 | x1+5x2 |
| 0,13 | 0,075 | -0,94445 | 0,1 | 0,205 | 0,505 |
| 0,26 | 0,15 | -1,8378 | 0,2 | 0,41 | 1,01 |
| 0,39 | 0,225 | -2,68005 | 0,3 | 0,615 | 1,515 |
| 0,52 | 0,3 | -3,4712 | 0,4 | 0,82 | 2,02 |
| 0,65 | 0,375 | -4,21125 | 0,5 | 1,025 | 2,525 |
| 0,78 | 0,45 | -4,9002 | 0,6 | 1,23 | 3,03 |
| 0,91 | 0,525 | -5,53805 | 0,7 | 1,435 | 3,535 |
| 1,04 | 0,6 | -6,1248 | 0,8 | 1,64 | 4,04 |
| 1,17 | 0,675 | -6,66045 | 0,9 | 1,845 | 4,545 |
| 1,183 | 0,6825 | -6,7112 | 0,91 | 1,8655 | 4,5955 |
| 1,196 | 0,69 | -6,76145 | 0,92 | 1,886 | 4,646 |
| 1,209 | 0,6975 | -6,81118 | 0,93 | 1,9065 | 4,6965 |
| 1,222 | 0,705 | -6,8604 | 0,94 | 1,927 | 4,747 |
| 1,235 | 0,7125 | -6,90911 | 0,95 | 1,9475 | 4,7975 |
| 1,248 | 0,72 | -6,95731 | 0,96 | 1,968 | 4,848 |
| 1,261 | 0,7275 | -7,005 | 0,97 | 1,9885 | 4,8985 |
| 1,274 | 0,735 | -7,05218 | 0,98 | 2,009 | 4,949 |
| 1,287 | 0,7425 | -7,09884 | 0,99 | 2,0295 | 4,9995 |
| 1,3 | 0,75 | -7,145 | 2,05 | 5,05 |
«Метод частичного улучшения по группам переменных в задачах нелинейной однокритериальной оптимизации».(МОИ)
Теоретическая часть.
Рассмотрим метод поочередного изменения переменных, который обычно называют методом Гаусса-Зайделя или методом частичного улучшения по группам переменных. При обычном методе Гаусса –Зайделя у оптимизируемой функции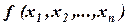 
фиксируются все аргументы, кроме одного, например, 
.
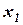Находится значение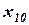 
такое, что
.
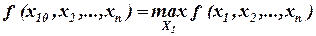Далее фиксируется 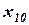и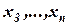 
. Находится 
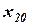такое, что 
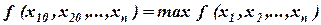, и т.д. Когда один цикл пройден, т. е. найдена точка 
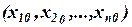, начинается новый цикл: фиксируются все переменные, кроме 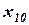и т.д. Неудобство метода заключается в его зависимости от выбора системы координат. Например, для квадратичной функции двух переменных, для которой линии уровня представляют собой эллипсы, оптимизация заканчивается за один цикл, если оси координат параллельны осям эллипсов уровня, и сводится к бесконечной последовательности циклов, если оси координат не параллельны осям эллипсов (рис. 1).
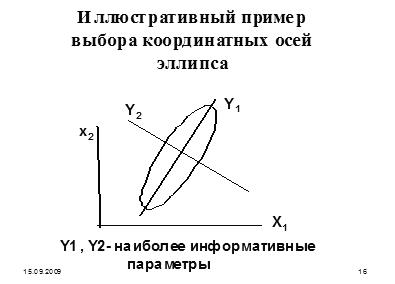
Демонстрационный пример частичного улучшения по группам переменных в задаче нелинейной однокритериальной оптимизации.
Вначале найдем решение стандартным методом, осуществляя поиск оптимума по всем переменным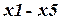 
.
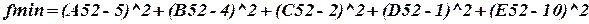
| A | B | C | D | E |
| x1 | x2 | x3 | x4 | x5 |
| x1+x2+x3+x4+x5<=??? | ||||
| x1<=4 | ||||
| x2<=3 | ||||
| x1+x2<=9 | ||||
| x3+x4<=3 | ||||
| fmin= |
Исходная таблица
·x1 - A52
·x2 - B52
·x3 - C52
·x4 - D52
·x5 - E52
Оптимальное решение имеет вид
| A | B | C | D | E |
| x1 | x2 | x3 | x4 | x5 |
| x1+x2+x3+x4+x5<=? | ||||
| x1<=4 | ||||
| x2<=3 | ||||
| x1+x2<=9 | ||||
| x3+x4<=3 | ||||
| fmin= |