Бірінші ретті сызықтық дифференциалдық теңдеулер.

Анықтама. 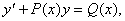түріндегі дифференциалдық теңдеу у жəне оның у' туындысына қатысты сызықтық деп аталады, ал егер оң жағы Q(x) нөлге тең болса, онда сызықтық біртекті, нөлге тең болмаса, онда сызықтық біртекті емес дифференциалдық теңдеу делінеді, мұндағы 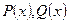- х-тан тəуелді берілген үзіліссіз функциялар.

І. Сызықтық біртекті дифференциалдық теңдеуді шешуді қарастырайық : //

.

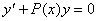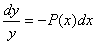
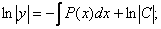
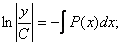
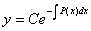
- сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі.

ІІ. Сызықтық біртекті емес дифференциалдық теңдеуді 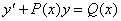шешудің тұрақтыны вариациялау (Лагранж) әдісінқарастырайық. Ол үшін біртекті теңдеудің жалпы шешімін табамыз:

.

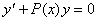
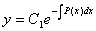Енді жалпы шешімдегі тұрақты С-ны х-тің функциясы деп қарастырамыз. Сонда:

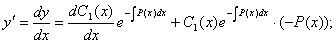
Алынған өрнекті берілген теңдеуге қоямыз:

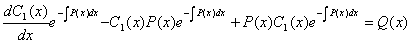
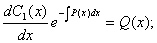
С₁(х)-ді табамыз:

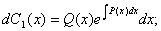
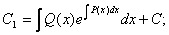
Берілген теңдеуге қоя отырып:

.

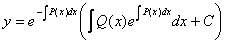сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімін аламыз.

Мысал 1: 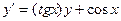- сызықтық біртекті емес дифференциалдық теңдеуді шеш.

Шешуі:

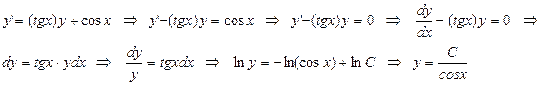
Мұндағы, 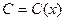- деп ұйғарамыз.

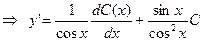
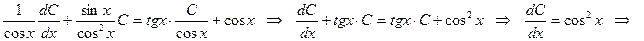
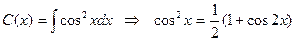болғандықтан

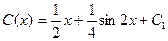
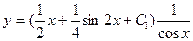- жалпы шешім.

Мысал 2: 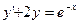сызықтық біртекті емес дифференциалдық теңдеуді шеш.

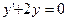біртекті дифференциалдық теңдеуді шешейік.

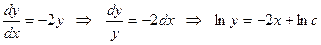
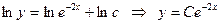
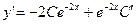
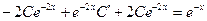
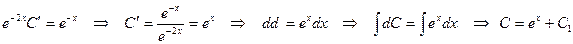
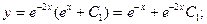
Мысал 3: 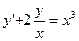- сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімін тап.

Шешуі:

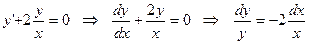
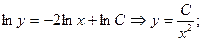мұндағы 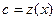делік.

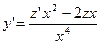
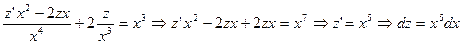
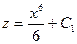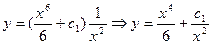, - сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі.

Кейде біртекті емес сызықты дифференциалдық теңдеуді шешу үшін 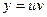алмастыруын (Бернулли әдісін)қолданамыз, яғни шешімді белгісіз екі функцияның көбейтіндісі түрінде іздейміз. Мұнда, туындыны 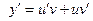өрнегімен алмастырамыз.

Мысал: А(а;а) нүктесі арқылы өтетін у=у(х) қисығы үшін келесі қасиет орындалсын: егер қисықтың кез келген М(х;у) нүктесінде Оу осін С нүктесінде қиятындай жанама жүргізсе, онда ОСМВ трапециясының ауданы тұрақты және а²-қа тең. Аталған қисықтың теңдеуін жаз.

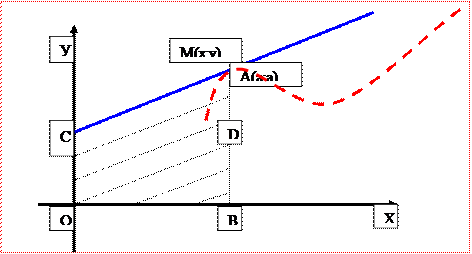
Шешуі:S_трап= 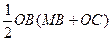екені белгілі, мұндағы MB=y; OB=x;

OC=BM-DM=BM-CDtgDCM=y-xy^/ болғандықтан, трапеция ауданының формуласынан:

а²= 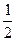х(у+у-ху^/) немесе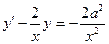

- сызықтық біртекті емес дифференциалдық теңдеу аламыз.

Оның шешімін Бернулли әдісімен табайық, яғни 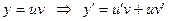алмастыруын жасайық. Теңдеуге апарып қойсақ:

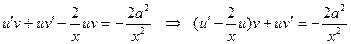
1)

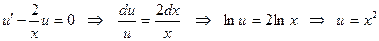
2)

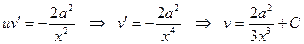
3) 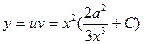- сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі, у(а)=а болғандықтан:

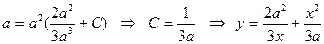- ізделінді қисықтың теңдеуі.

Бернулли теңдеуі

Aнықтама. 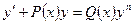түріндегі дифференциалдық теңдеу Бернулли теңдеуі деп аталады, мұндағы 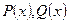- берілген үзіліссіз функциялар, n≠0, n≠1

Бернулли теңдеуінің сызықтық теңдеуден айырмашылығы оң жақ бөлігінде у-тің белгілі бір дəрежесі бар, шешілуі сызықтық теңдеулердегідей жүргізіледі. Шешімін табу үшін теңдеудің екі жағында 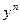-ге бөлеміз:

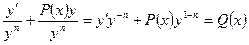(1).

Алмастыру жасаймыз: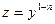

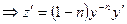
Шыққан мәнді (1) теңдікке қоямыз:

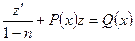
- бірінші ретті сызықтық дифференциалдық теңдеу.

Шыққан теңдеуді шеше отырып z-ті табамыз, z-тің табылған мәнін жасаған алмастыруымызға қойып, Бернулли теңдеуінің шешімін табамыз.

Мысал 1: 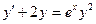- Бернулли теңдеуін шеш.

Шешуі:

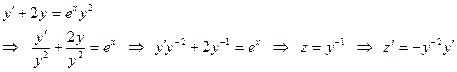
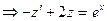
Алынған сызықтық дифференциалдық теңдеуді шешу үшін тұрақтыны вариациялау әдісін қолданамыз.

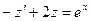немесе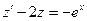

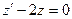-біртекті сызықты дифференциалдық теңдеу

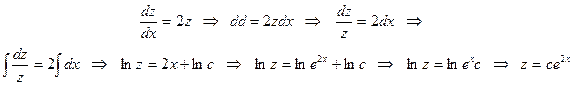(4)

Енді тұрақты с-ны қандайда бір х-қа тәуелді функция деп аламыз, яғни

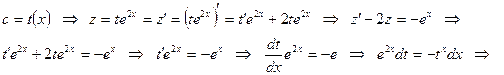
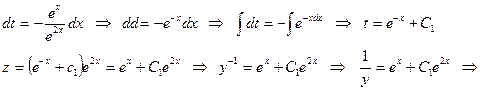
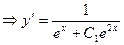
- Бернулли теңдеуінің жалпы шешімі.